What Is 15 Of 60
marihuanalabs
Sep 22, 2025 · 5 min read
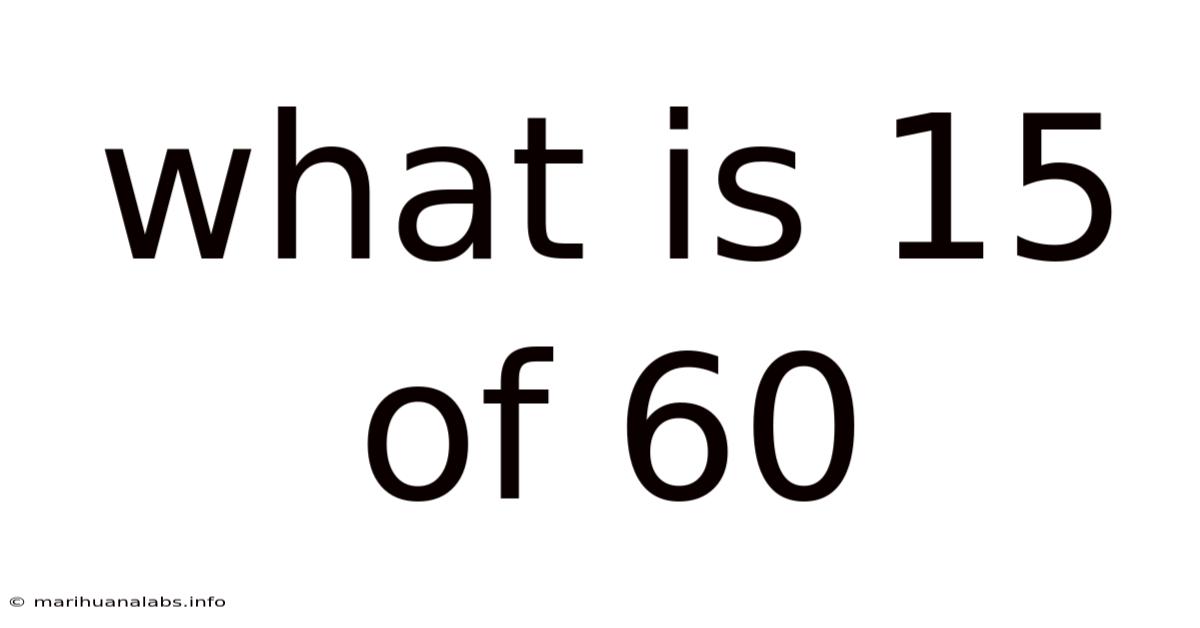
Table of Contents
What is 15 of 60? Unpacking Fractions, Percentages, and Ratios
This seemingly simple question, "What is 15 of 60?", opens a door to a world of mathematical concepts that underpin many aspects of our daily lives. Understanding how to solve this problem goes beyond simply finding the answer; it’s about grasping the fundamental principles of fractions, percentages, and ratios, and how they interconnect. This article will not only provide the solution but also delve into the underlying mathematical principles, offering a comprehensive understanding suitable for various learning levels. We’ll explore different approaches, ensuring you gain a solid grasp of these essential concepts.
Understanding the Core Concepts
Before diving into the solution, let's establish a clear understanding of the key mathematical ideas involved:
-
Fractions: A fraction represents a part of a whole. It's expressed as a numerator (the top number) over a denominator (the bottom number). In our case, "15 of 60" can be represented as the fraction 15/60.
-
Percentages: A percentage is a fraction expressed as a part of 100. It's denoted by the symbol "%". To find a percentage, we express the fraction as an equivalent fraction with a denominator of 100 or we convert the fraction to a decimal and multiply by 100.
-
Ratios: A ratio compares two or more quantities. It can be expressed as a fraction, using a colon (:), or using the word "to". In our problem, the ratio of 15 to 60 can be written as 15/60, 15:60, or 15 to 60.
These three concepts are intrinsically linked. A fraction can be expressed as a percentage and a ratio, and vice-versa. Understanding their interrelationships is crucial for solving problems like "What is 15 of 60?".
Calculating 15 of 60: Multiple Approaches
There are several ways to determine what 15 represents as a proportion of 60. Let's explore the most common methods:
1. Simplifying the Fraction:
The most straightforward approach is to express "15 of 60" as a fraction (15/60) and simplify it to its lowest terms. We find the greatest common divisor (GCD) of 15 and 60, which is 15. Dividing both the numerator and the denominator by 15, we get:
15/60 = (15 ÷ 15) / (60 ÷ 15) = 1/4
This means that 15 is one-quarter (1/4) of 60.
2. Converting to a Percentage:
To express 15/60 as a percentage, we can follow these steps:
-
Convert the fraction to a decimal: Divide the numerator (15) by the denominator (60): 15 ÷ 60 = 0.25
-
Multiply the decimal by 100: 0.25 × 100 = 25%
Therefore, 15 is 25% of 60.
3. Using Ratio Proportions:
We can also solve this using ratio proportions. We can set up a proportion:
15/60 = x/100
Where 'x' represents the percentage. To solve for 'x', we cross-multiply:
60x = 1500
x = 1500/60 = 25
Again, this confirms that 15 is 25% of 60.
4. Using Mental Math:
For those comfortable with mental calculations, you can recognize that 60 is four times 15 (60/15 = 4). This immediately tells you that 15 is 1/4 or 25% of 60. This method demonstrates the importance of number sense and pattern recognition in mathematics.
Real-World Applications
The concept of finding a proportion, whether expressed as a fraction, percentage, or ratio, has countless applications in everyday life. Here are just a few examples:
- Shopping: Calculating discounts (e.g., 25% off a $60 item).
- Cooking: Adjusting recipes (e.g., using 15 ml of oil instead of the original 60 ml).
- Finance: Determining interest rates or calculating loan payments.
- Science: Analyzing experimental data and expressing results as percentages or ratios.
- Construction: Scaling drawings and plans.
Expanding the Understanding: Further Exploration
While solving "What is 15 of 60?" provides a basic understanding of fractions, percentages, and ratios, let's delve deeper into related mathematical concepts:
-
Equivalent Fractions: Understanding that 15/60, 1/4, 25/100, and 0.25 all represent the same proportion is crucial for mathematical fluency.
-
Decimal Representation: Converting fractions to decimals and vice versa is a fundamental skill. Practice converting different fractions to decimals to reinforce this understanding.
-
Percentage Increase and Decrease: Expanding on percentages, learn how to calculate percentage increases and decreases – this is vital for understanding growth and decline in various contexts.
Frequently Asked Questions (FAQ)
Q1: What if the numbers were larger or more complex?
The same principles apply. Regardless of the size of the numbers, you can always simplify the fraction to its lowest terms, convert it to a percentage, or use ratio proportions to find the answer. Using a calculator can aid in the calculations, especially with larger numbers.
Q2: Are there other ways to solve this problem?
Yes, there are many methods. The key is finding the approach that suits your understanding and comfort level. You could also use visual aids like pie charts or bar graphs to represent the proportion.
Q3: Why is understanding this important?
Understanding proportions is fundamental to numeracy and problem-solving skills. These concepts are used in various fields, from everyday tasks to complex scientific calculations.
Conclusion: Mastering the Fundamentals
This seemingly simple question, "What is 15 of 60?", has led us on a journey through the interconnected world of fractions, percentages, and ratios. By mastering these fundamental concepts, you equip yourself with essential tools for problem-solving in various contexts. Remember, the key is not just to find the answer (which is 1/4 or 25%) but to understand the underlying principles and their practical applications. Continue practicing different approaches and tackling various problems to strengthen your mathematical skills. The more you practice, the more intuitive and effortless these calculations will become. Keep exploring, keep learning, and keep applying these skills to real-world situations to truly master this core mathematical concept.
Latest Posts
Latest Posts
-
How To Draw Spain Flag
Sep 23, 2025
-
Global Developmental Delay In Adults
Sep 23, 2025
-
Standard Life Shares Price Today
Sep 23, 2025
-
Column Of The Holy Trinity
Sep 23, 2025
-
What Is 5 Of 180
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.