What Is 15 Of 300
marihuanalabs
Sep 17, 2025 · 5 min read
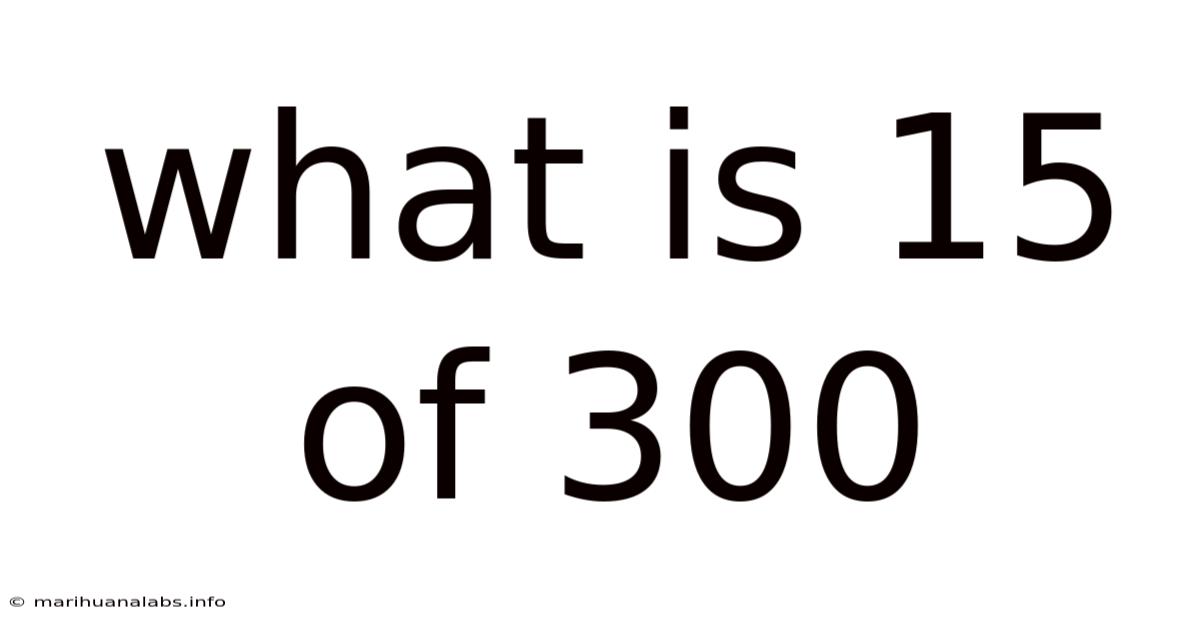
Table of Contents
What is 15% of 300? A Deep Dive into Percentages and Their Applications
Finding 15% of 300 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages opens doors to a wide range of applications in everyday life, from calculating discounts and taxes to understanding statistical data and financial reports. This article will not only answer the question directly but also explore the various methods for solving percentage problems, provide practical examples, and delve into the broader significance of percentages in different fields.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to represent percentages. Essentially, it represents a portion of a whole. For instance, 15% means 15 parts out of 100, or 15/100, which simplifies to 3/20. Understanding this fundamental concept is key to solving percentage problems efficiently.
Method 1: Using Decimal Conversion
The most straightforward way to calculate 15% of 300 is to convert the percentage to a decimal and then multiply.
-
Step 1: Convert the percentage to a decimal: To convert 15% to a decimal, divide it by 100: 15% ÷ 100 = 0.15
-
Step 2: Multiply the decimal by the whole number: Multiply the decimal (0.15) by the number you want to find the percentage of (300): 0.15 x 300 = 45
Therefore, 15% of 300 is 45.
Method 2: Using Fractions
As mentioned earlier, 15% can be expressed as the fraction 15/100, which simplifies to 3/20. This fractional representation offers an alternative approach.
-
Step 1: Express the percentage as a fraction: 15% = 15/100 = 3/20
-
Step 2: Multiply the fraction by the whole number: Multiply the fraction (3/20) by the whole number (300): (3/20) x 300 = 3 x (300/20) = 3 x 15 = 45
Again, the result is 45. This method highlights the relationship between percentages, fractions, and decimals.
Method 3: Using Proportions
The concept of proportions offers a more generalized approach to solving percentage problems. We can set up a proportion to solve for the unknown value.
-
Step 1: Set up a proportion: We can set up a proportion as follows: 15/100 = x/300, where 'x' represents the unknown value (15% of 300).
-
Step 2: Cross-multiply: Cross-multiplying gives us: 100x = 15 * 300 = 4500
-
Step 3: Solve for x: Divide both sides by 100: x = 4500/100 = 45
Once again, we find that 15% of 300 is 45. This method is particularly useful when dealing with more complex percentage problems.
Practical Applications of Percentages
The ability to calculate percentages is crucial in various real-world scenarios:
-
Retail Discounts: Imagine a store offering a 15% discount on a $300 item. Using the methods described above, you can easily calculate the discount amount ($45) and the final price ($255).
-
Sales Tax Calculations: Many countries impose sales tax on goods and services. If the sales tax is 15%, you can calculate the tax amount on a $300 purchase using the same percentage calculation techniques.
-
Financial Analysis: Percentages are extensively used in financial analysis to represent growth rates, profit margins, and return on investments. Understanding percentage changes helps in comparing financial performance over time.
-
Statistical Analysis: Percentages are used to represent proportions and frequencies in statistical data. For example, expressing the percentage of a population with certain characteristics.
-
Scientific Research: In scientific research, percentages often describe experimental results, error margins, and the proportion of samples showing a particular outcome.
Beyond the Basics: Understanding Percentage Increase and Decrease
While finding a percentage of a number is essential, understanding percentage increase and decrease is equally important.
Let's say a quantity increases by 15%. To calculate the new value, you would add the percentage increase to the original value. For example, if a $300 investment increases by 15%, the new value is $300 + ($300 x 0.15) = $345.
Conversely, if a quantity decreases by 15%, you would subtract the percentage decrease from the original value. If a $300 item is discounted by 15%, the new price is $300 - ($300 x 0.15) = $255.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a different percentage of 300?
A: You can use the same methods (decimal conversion, fractions, or proportions) by substituting the desired percentage for 15%. Simply replace 0.15 or 15/100 with the new percentage expressed as a decimal or fraction.
-
Q: Can I use a calculator to solve percentage problems?
A: Absolutely! Most calculators have a percentage function (%) that simplifies these calculations. You can input the problem directly as "15% of 300" or perform the calculations step-by-step.
-
Q: Are there any online tools to help with percentage calculations?
A: Yes, numerous online calculators and websites are available to assist with percentage calculations. These tools can be particularly helpful for more complex problems or when you need quick results.
-
Q: How can I improve my understanding of percentages?
A: Practice is key. Try solving various percentage problems with different numbers and percentages. You can find practice problems in textbooks, online, or even create your own scenarios using real-life examples.
Conclusion: The Importance of Mastering Percentages
Understanding percentages is a fundamental skill that extends far beyond simple arithmetic calculations. It's a crucial tool for navigating daily life, making informed decisions, and comprehending information across diverse fields. Mastering the various methods for calculating percentages, whether using decimals, fractions, or proportions, provides a versatile skillset applicable to numerous situations. From calculating discounts and taxes to interpreting statistical data and analyzing financial reports, the ability to work with percentages efficiently is an invaluable asset. Remember, consistent practice and application will solidify your understanding and make percentage calculations second nature.
Latest Posts
Latest Posts
-
All Talk And No Action
Sep 17, 2025
-
Human Features Of North America
Sep 17, 2025
-
Hansel And Gretel Get Baked
Sep 17, 2025
-
Code Of Conduct Veterinary Nurses
Sep 17, 2025
-
Dubai Map In World Map
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 300 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.