What Is 15 Of 25
marihuanalabs
Sep 10, 2025 · 5 min read
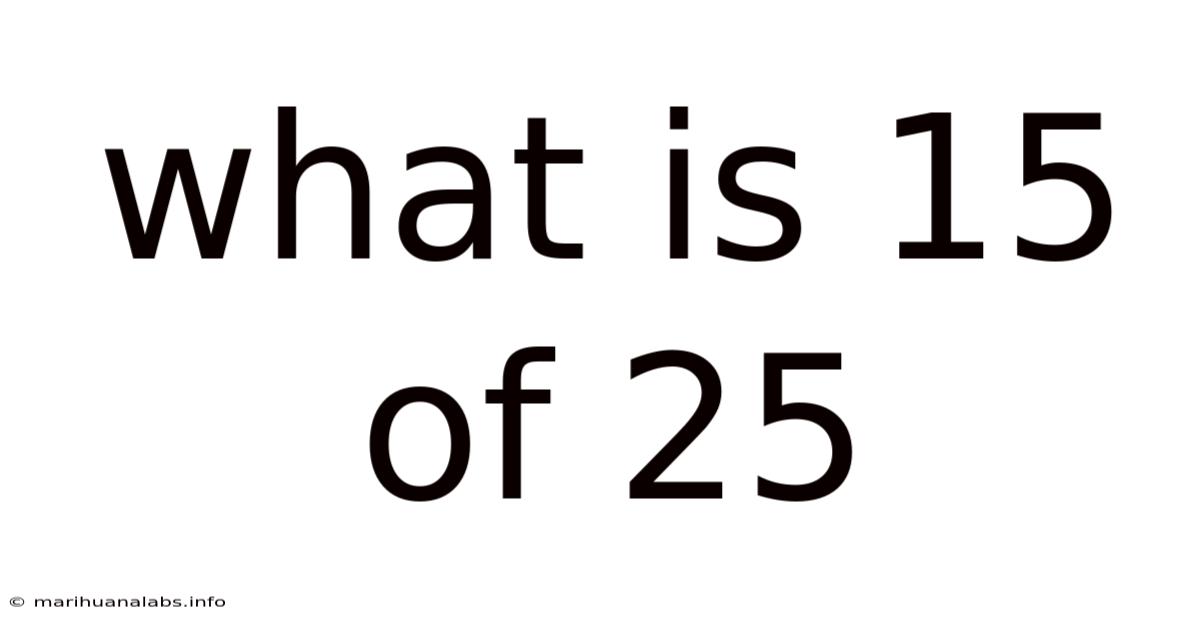
Table of Contents
What is 15 of 25? Deconstructing Fractions, Percentages, and Ratios
This article delves into the seemingly simple question: "What is 15 of 25?" While the immediate answer might seem obvious, a deeper exploration reveals a wealth of mathematical concepts crucial for understanding fractions, percentages, ratios, and their practical applications in everyday life. We'll not only find the answer but also explore the underlying principles, providing a solid foundation for more complex mathematical problems.
Understanding the Basics: Fractions and Ratios
At its core, "15 of 25" represents a fraction. A fraction is a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In this case, 15 is the numerator and 25 is the denominator. This fraction, 15/25, signifies that we're considering 15 units out of a total of 25 units.
The fraction 15/25 is also a ratio, expressing the relationship between two quantities. It tells us that there are 15 units for every 25 units in total. Understanding this relationship is key to solving many problems involving proportions and scaling.
Calculating the Value: Simplifying the Fraction
The fraction 15/25 can be simplified by finding the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both 15 and 25 without leaving a remainder. In this case, the GCD is 5. To simplify the fraction, we divide both the numerator and denominator by the GCD:
15 ÷ 5 = 3 25 ÷ 5 = 5
Therefore, 15/25 simplifies to 3/5. This means that 15 out of 25 is equivalent to 3 out of 5. This simplified fraction represents the same proportion, but in a more concise form.
Expressing the Value as a Percentage
Percentages are another way to represent parts of a whole. A percentage expresses a fraction as a portion of 100. To convert the fraction 3/5 to a percentage, we perform the following calculation:
(3/5) * 100% = 60%
Therefore, 15 out of 25 is equal to 60%. This means that 15 represents 60% of the total 25 units. Percentages are frequently used to express proportions in various contexts, including grades, discounts, and statistical data.
Real-World Applications: Illustrative Examples
The concept of "15 of 25" finds applications in numerous real-world scenarios:
- Test Scores: If a student answers 15 questions correctly out of a total of 25, their score is 60%.
- Sales and Discounts: If a store offers a discount of 15 items out of a total of 25 items, it represents a 60% discount.
- Surveys and Statistics: If 15 out of 25 respondents agree with a particular statement, the agreement rate is 60%.
- Inventory Management: If a warehouse has 25 units of a product and 15 have been sold, 60% of the inventory has been sold.
- Recipe Scaling: If a recipe calls for 25 units of an ingredient and you want to reduce it to 15 units, you are using 60% of the original recipe.
Beyond the Basics: Exploring Decimal Representation
The fraction 3/5 can also be expressed as a decimal by dividing the numerator by the denominator:
3 ÷ 5 = 0.6
Therefore, 15 out of 25 is equivalent to 0.6. Decimals are useful for precise calculations and comparisons, especially in fields like finance and engineering.
Advanced Concepts: Proportions and Ratios
The problem "15 of 25" can also be viewed through the lens of proportions. A proportion is a statement that two ratios are equal. For example:
15/25 = x/100
To solve for x, which represents the percentage, we cross-multiply:
15 * 100 = 25 * x 1500 = 25x x = 1500/25 x = 60
This confirms that 15 out of 25 is equal to 60%. Understanding proportions is vital for solving various problems involving scaling, ratios, and similar triangles.
Frequently Asked Questions (FAQ)
Q1: Can I simplify 15/25 any further than 3/5?
A1: No, 3/5 is the simplest form of the fraction because the numerator and denominator have no common divisors other than 1.
Q2: What if I have a similar problem, but with different numbers? How can I approach it?
A2: Follow the same steps: 1. Express the problem as a fraction. 2. Simplify the fraction by finding the GCD of the numerator and denominator. 3. Convert the simplified fraction to a percentage by multiplying by 100%. 4. Optionally, convert the fraction to a decimal by performing the division.
Q3: Are there any online calculators or tools that can help me solve these types of problems?
A3: Yes, many online calculators are available that can simplify fractions, convert fractions to percentages, and perform other related calculations. Simply search for "fraction calculator" or "percentage calculator" online.
Q4: Why is it important to learn about fractions, percentages, and ratios?
A4: These mathematical concepts are fundamental to understanding proportions, ratios, and various real-world applications in diverse fields, including finance, science, engineering, and everyday life. They are essential for problem-solving, making informed decisions, and interpreting data.
Conclusion: Mastering the Fundamentals
The question "What is 15 of 25?" serves as a gateway to understanding fundamental mathematical concepts. Through this exploration, we've seen how a simple fraction can be simplified, converted to a percentage and a decimal, and applied to various real-world situations. Mastering these concepts provides a robust foundation for tackling more complex mathematical challenges and enhances your ability to analyze and interpret data effectively in various contexts. Remember that practice is key—the more you work with fractions, percentages, and ratios, the more comfortable and proficient you will become. Don't be afraid to experiment with different numbers and apply these concepts to problems you encounter in your daily life.
Latest Posts
Latest Posts
-
1 Out Of 8 Percentage
Sep 10, 2025
-
Stories About Myths And Legends
Sep 10, 2025
-
Whats Bigger Kilobytes Or Megabytes
Sep 10, 2025
-
Descriptive Words For The Beach
Sep 10, 2025
-
Macbeth Act 3 Scene 2
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.