What Is 15 Of 100
marihuanalabs
Sep 10, 2025 · 6 min read
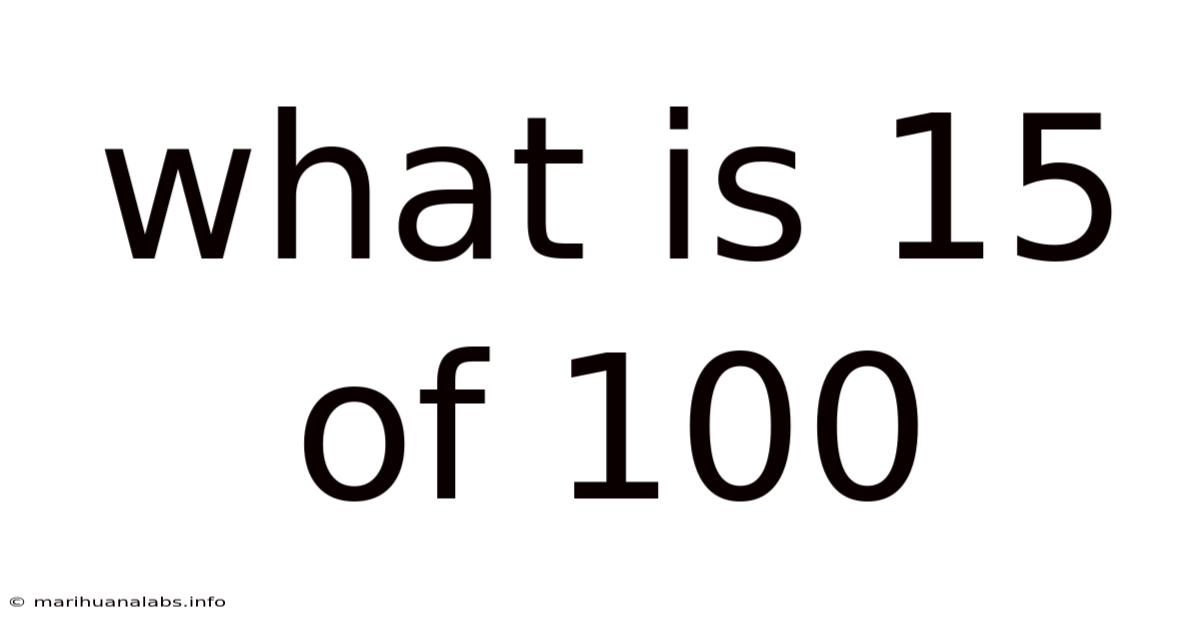
Table of Contents
What is 15 of 100? Understanding Percentages and Fractions
What is 15 of 100? This seemingly simple question opens the door to understanding fundamental mathematical concepts like percentages, fractions, and ratios. It's a question that appears frequently in everyday life, from calculating discounts and sales tax to understanding statistics and probabilities. This comprehensive guide will not only answer the question directly but also explore the underlying principles and practical applications, equipping you with a solid grasp of these essential mathematical tools.
Understanding Percentages: A Foundation in Mathematics
A percentage is simply a fraction or a ratio expressed as a number out of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 15 of 100 is equivalent to 15% (fifteen percent). This means 15 out of every 100 parts of a whole.
To understand this better, imagine you have 100 apples. If 15 of those apples are red, then 15% of your apples are red. This simple example illustrates the core concept of percentages – representing a portion of a whole as a number out of 100.
Expressing 15 of 100 as a Fraction
Percentages are closely related to fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (the top number) and the denominator (the bottom number). In the context of "15 of 100," the fraction is expressed as 15/100. This means 15 parts out of a total of 100 parts.
This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 15 and 100 is 5. Dividing both the numerator and the denominator by 5, we get the simplified fraction 3/20. Both 15/100 and 3/20 represent the same proportion or value.
Decimal Representation of 15 of 100
Percentages and fractions can also be expressed as decimals. To convert a fraction to a decimal, simply divide the numerator by the denominator. In this case, 15/100 = 0.15. This decimal representation is another way to express the same proportion.
The decimal form is particularly useful in calculations involving percentages, especially when using calculators or computers. It provides a straightforward numerical representation that's readily used in various computations.
Calculating Percentages: Practical Applications
Understanding how to calculate percentages is crucial in various real-world scenarios. Here are a few examples:
-
Discounts: If a store offers a 15% discount on a $100 item, the discount amount is calculated as 15% of $100, which is (15/100) * $100 = $15. The final price would be $100 - $15 = $85.
-
Sales Tax: If the sales tax in your area is 15%, and you buy an item for $100, the sales tax amount would be (15/100) * $100 = $15. The total cost would be $100 + $15 = $115.
-
Grades and Scores: If you answered 15 out of 100 questions correctly on a test, your score is 15%, indicating your performance relative to the total number of questions.
-
Statistics and Data Analysis: Percentages are essential for analyzing and interpreting data. For example, if a survey shows that 15% of respondents prefer a particular product, this provides valuable insights into consumer preferences.
-
Financial Calculations: Percentages are widely used in finance for calculating interest rates, returns on investment, and other financial metrics.
Beyond the Basics: Proportions and Ratios
The concept of "15 of 100" extends beyond simple percentages. It introduces the broader idea of proportions and ratios. A ratio is a comparison of two quantities, while a proportion is a statement of equality between two ratios.
The ratio 15:100 (15 to 100) can be simplified to 3:20 (3 to 20), just like the fraction. This means for every 3 parts of one quantity, there are 20 parts of another quantity. This simplified ratio maintains the same proportional relationship as the original 15:100.
Working with Different Numbers: Applying the Principle
The principle of calculating a percentage remains consistent even if the total number changes. Let's say we have 200 apples, and 30 are red. To find the percentage of red apples, we follow the same process:
- Set up the fraction: 30/200
- Simplify the fraction: 3/20
- Convert to a decimal: 3/20 = 0.15
- Convert to a percentage: 0.15 * 100% = 15%
Despite having a different total number of apples (200 instead of 100), the percentage of red apples remains 15%. This demonstrates that the percentage represents a consistent proportion regardless of the total quantity.
Advanced Applications: Compound Interest and Growth Rates
Percentages become even more powerful when used in complex calculations, such as compound interest and growth rates. Compound interest involves earning interest not only on the principal amount but also on the accumulated interest. Understanding percentages is critical for calculating future values, analyzing investments, and making informed financial decisions.
Growth rates, whether in population, economics, or other fields, often use percentages to express the rate of change over time. For instance, a 15% annual growth rate indicates a 15% increase in the quantity each year.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a percentage and a fraction?
A1: Both percentages and fractions represent parts of a whole. However, a percentage is always expressed as a number out of 100, while a fraction can be any ratio of two numbers. Percentages are essentially fractions with a denominator of 100.
Q2: How can I easily convert a percentage to a decimal?
A2: To convert a percentage to a decimal, simply divide the percentage by 100. For example, 15% becomes 15/100 = 0.15.
Q3: How do I convert a fraction to a percentage?
A3: To convert a fraction to a percentage, first convert it to a decimal by dividing the numerator by the denominator. Then, multiply the decimal by 100 and add the % symbol. For example, 3/20 = 0.15; 0.15 * 100% = 15%.
Q4: Can I use a calculator to work with percentages?
A4: Absolutely! Calculators make percentage calculations much easier, especially for complex problems. Most calculators have a percentage button (%) that simplifies the process.
Q5: Are percentages always expressed as whole numbers?
A5: No, percentages can be expressed as decimals or fractions as well. For example, 15.5% or 15 1/2 % are valid representations.
Conclusion: Mastering the Fundamentals
Understanding "what is 15 of 100" transcends a simple arithmetic problem. It provides a gateway to mastering percentages, fractions, decimals, ratios, and proportions – concepts fundamental to numerous aspects of life. From everyday shopping to complex financial modeling, the ability to work confidently with percentages is an invaluable skill. By grasping the underlying principles and practicing their application, you can build a strong mathematical foundation and enhance your problem-solving abilities in various contexts. The ability to effortlessly convert between percentages, fractions, and decimals allows for a flexible and adaptable approach to tackling numerical challenges, empowering you to navigate the quantitative world with greater ease and understanding.
Latest Posts
Latest Posts
-
Tin Man By Sarah Winman
Sep 10, 2025
-
What Wax Is Made Of
Sep 10, 2025
-
Synopsis Of Les Miserables Musical
Sep 10, 2025
-
13k Is How Many Miles
Sep 10, 2025
-
Repeated Measures Design In Psychology
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.