What Is 10 Of 80
marihuanalabs
Sep 14, 2025 · 5 min read
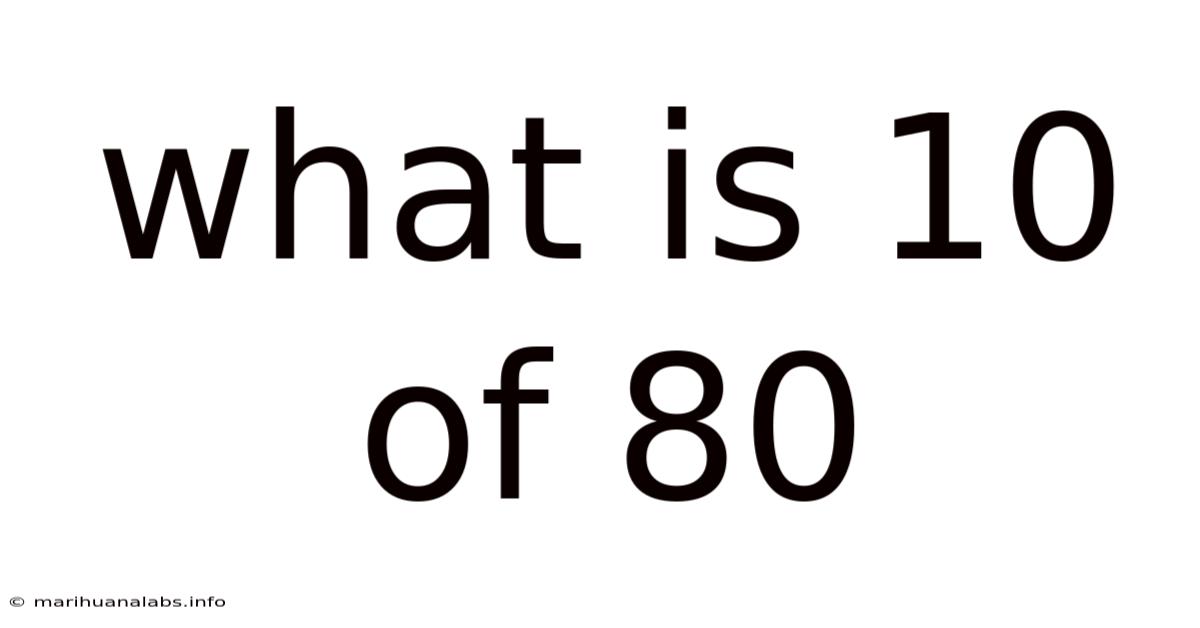
Table of Contents
What is 10% of 80? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will thoroughly explore the question "What is 10% of 80?" and, in doing so, provide a comprehensive overview of percentage calculations, their underlying principles, and their relevance in various contexts. We will not just provide the answer but delve into the why and how, ensuring a complete understanding of the concept.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol used to represent percentage is "%". Essentially, it represents a proportion of a whole. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5. Understanding this basic definition is crucial for grasping percentage calculations.
Calculating 10% of 80: The Direct Approach
The most straightforward way to calculate 10% of 80 is to use the following formula:
Percentage × Whole Number = Result
In this case:
10% × 80 = ?
First, convert the percentage to a decimal by dividing by 100:
10% ÷ 100 = 0.10
Now, multiply the decimal by the whole number:
0.10 × 80 = 8
Therefore, 10% of 80 is 8.
Alternative Methods: Understanding the Flexibility of Percentage Calculations
While the direct method is efficient, understanding alternative approaches provides a deeper grasp of the concept and can be helpful in more complex scenarios.
- Fraction Method: Percentages can be easily converted into fractions. 10% is equivalent to 10/100, which simplifies to 1/10. To find 10% of 80, we can multiply 80 by 1/10:
(1/10) × 80 = 80/10 = 8
This method highlights the direct relationship between fractions and percentages.
- Proportion Method: This method uses the concept of ratios. We can set up a proportion:
10/100 = x/80
Cross-multiplying, we get:
10 × 80 = 100 × x
800 = 100x
x = 800/100 = 8
This approach is particularly useful when dealing with more complex percentage problems.
Real-World Applications: Where Percentages Matter
The calculation of 10% of 80, seemingly simple, has far-reaching applications in numerous real-world situations:
-
Discounts: Imagine a store offering a 10% discount on an item priced at $80. Using our calculation, the discount amount is $8, resulting in a final price of $72.
-
Taxes: A 10% sales tax on an $80 purchase would add $8 to the total cost, resulting in a final price of $88.
-
Tips: Calculating a 10% tip on an $80 meal is also straightforward; the tip amount would be $8.
-
Interest: If you invest $80 and earn a 10% annual interest, you would earn $8 in interest after one year.
-
Statistics and Data Analysis: Percentages are fundamental in representing and interpreting data. For example, if 10% of 80 survey respondents answered "yes" to a question, this means 8 respondents answered affirmatively.
-
Financial Statements: Financial reports extensively use percentages to represent various financial ratios, such as profit margins, debt-to-equity ratios, and return on investment (ROI). Understanding percentages is essential for interpreting these reports effectively.
Expanding the Understanding: Calculating Other Percentages of 80
While we’ve focused on 10%, let's explore how to calculate other percentages of 80 to further solidify the understanding of percentage calculations.
- Calculating 25% of 80:
25% = 0.25
0.25 × 80 = 20
- Calculating 50% of 80:
50% = 0.50
0.50 × 80 = 40
- Calculating 75% of 80:
75% = 0.75
0.75 × 80 = 60
- Calculating 100% of 80:
100% = 1
1 × 80 = 80
These examples illustrate the flexibility and consistent application of percentage calculations. Regardless of the percentage, the underlying principle remains the same: convert the percentage to a decimal and multiply by the whole number.
Beyond the Basics: Tackling More Complex Percentage Problems
While calculating a simple percentage like 10% of 80 is relatively straightforward, real-world scenarios often involve more complex calculations. Understanding these complexities is crucial for practical application.
-
Finding the Percentage: Instead of finding the percentage of a number, you might need to determine what percentage one number is of another. For example, what percentage is 8 of 80? To solve this, divide 8 by 80 and multiply by 100: (8/80) × 100 = 10%.
-
Finding the Whole Number: You might know the percentage and the result, but need to find the original whole number. For instance, if 10% of a number is 8, what is the number? To solve this, divide 8 by 0.10: 8/0.10 = 80.
-
Percentage Increase/Decrease: These calculations involve finding the percentage change between two numbers. For example, if a price increases from $80 to $88, the percentage increase is calculated as follows: [(88-80)/80] × 100 = 10%.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest from previous periods. It's a more complex calculation that utilizes the concept of percentages repeatedly.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages?
A: The easiest way is to convert the percentage to a decimal (by dividing by 100) and then multiply it by the whole number.
-
Q: Why are percentages important?
A: Percentages provide a standardized way to compare and understand proportions, making it easier to analyze data, make comparisons, and make informed decisions in various aspects of life.
-
Q: Can I use a calculator for percentage calculations?
A: Yes, most calculators have a percentage function that simplifies the calculation. However, understanding the underlying principles is crucial even when using a calculator.
-
Q: Are there any online tools to calculate percentages?
A: Yes, numerous online percentage calculators are available that can perform various percentage calculations. However, it's beneficial to learn the manual calculation process for a deeper understanding.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a fundamental skill that extends far beyond simple mathematical calculations. From managing personal finances to interpreting complex data, a solid grasp of percentages empowers informed decision-making in various aspects of life. This article has not only answered the question "What is 10% of 80?" but also provided a comprehensive exploration of percentage calculations, their applications, and how to approach more complex problems. By mastering this fundamental concept, you equip yourself with a valuable tool for navigating the quantitative world around us. Remember, the key is understanding the underlying principles and practicing different calculation methods to build confidence and proficiency.
Latest Posts
Latest Posts
-
Happy Face Sad Face Tattoo
Sep 14, 2025
-
Concave Graph Vs Convex Graph
Sep 14, 2025
-
Food Chain With A Lion
Sep 14, 2025
-
Catholicism Vs Protestantism Vs Orthodoxy
Sep 14, 2025
-
Bund Sightseeing Tunnel Shanghai China
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.