What Is 10 Of 50000
marihuanalabs
Sep 16, 2025 · 5 min read
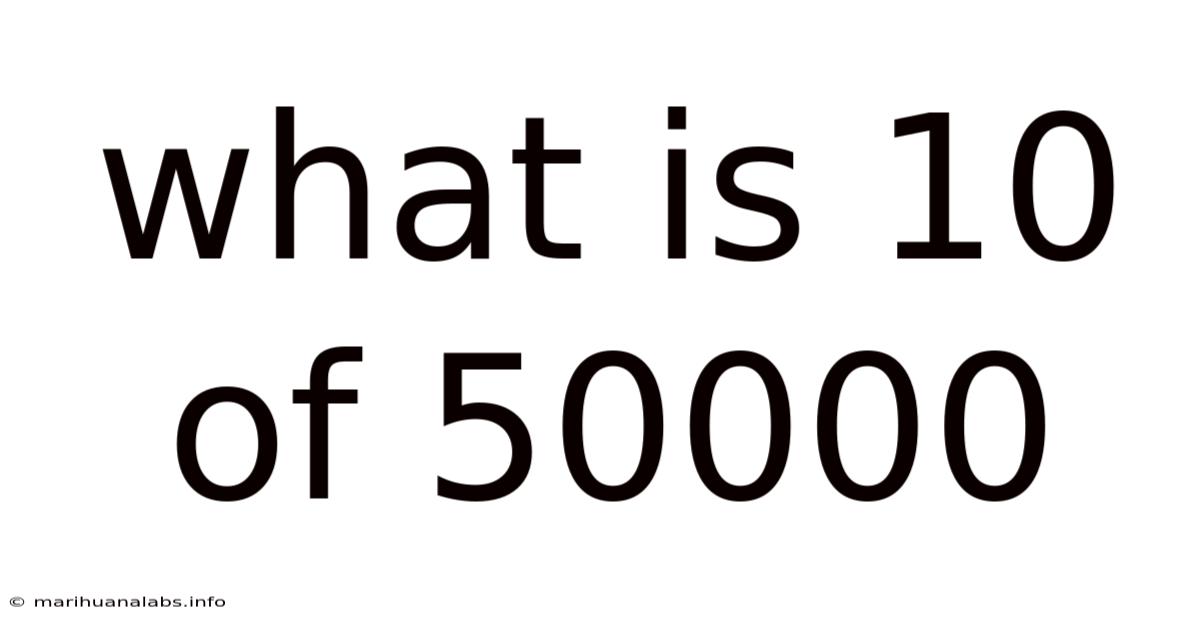
Table of Contents
What is 10/50000? Understanding Fractions, Percentages, and Decimals
This article delves into the seemingly simple question: "What is 10/50000?" While the answer might seem immediately obvious – a simple division problem – we'll unpack this calculation to explore the underlying concepts of fractions, percentages, and decimals, offering a deeper understanding of numerical relationships. This will be particularly helpful for anyone needing to grasp these concepts in various contexts, from basic arithmetic to more advanced mathematical applications.
Understanding Fractions: The Building Blocks
The expression 10/50000 is a fraction. A fraction represents a part of a whole. The number on top (10) is called the numerator, representing the part we're interested in. The number on the bottom (50000) is the denominator, representing the whole. In our case, we're considering 10 as a part of a whole of 50000.
Understanding fractions is fundamental to many areas of life. Think about sharing a pizza: if you have a pizza cut into 8 slices and you eat 2, you've eaten 2/8 (or 1/4) of the pizza. The fraction expresses the relationship between the part you ate (2) and the total number of slices (8).
Simplifying Fractions: Finding the Essence
Before calculating the decimal or percentage equivalent, it's often helpful to simplify the fraction. This involves finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by it. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
In our case, the GCD of 10 and 50000 is 10. Dividing both the numerator and denominator by 10, we get:
10/10 = 1 50000/10 = 5000
This simplifies our fraction to 1/5000. This simplified fraction is equivalent to 10/50000; it represents the same proportion or ratio. Simplifying fractions makes them easier to work with and understand.
Converting to Decimals: A Numerical Representation
To convert a fraction to a decimal, we simply divide the numerator by the denominator. Using a calculator or performing long division, we find:
1 ÷ 5000 = 0.0002
Therefore, 10/50000 (or 1/5000) is equal to 0.0002. The decimal representation gives us a more concrete numerical value, easily understandable in many contexts, especially those involving measurements or calculations.
Converting to Percentages: Expressing Proportion
Percentages are a common way to express proportions. A percentage represents a fraction out of 100. To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol.
0.0002 × 100 = 0.02%
Thus, 10/50000 is equivalent to 0.02%. This representation indicates that 10 is a very small portion (0.02%) of 50000. This is a useful way to understand the relative size of the fraction within the whole.
Real-World Applications: Understanding the Significance
Understanding how to calculate and interpret fractions, decimals, and percentages is crucial in many real-world scenarios:
- Finance: Calculating interest rates, discounts, and profit margins all involve working with fractions and percentages. Understanding the proportion of a loan or investment relative to the total is fundamental.
- Science: Many scientific measurements and calculations rely on expressing quantities as fractions or decimals. For instance, measuring concentrations of solutions or analyzing statistical data frequently uses these concepts.
- Engineering: Engineering designs involve precise calculations using fractions and decimals, ensuring accuracy in dimensions, materials, and performance.
- Everyday Life: Dividing resources fairly, understanding sales discounts, or calculating cooking ingredients often necessitates these numerical skills.
Further Exploration: Ratios and Proportions
The fraction 10/50000 can also be understood as a ratio. A ratio expresses the relationship between two quantities. In this case, the ratio of 10 to 50000 can be written as 10:50000 or, in its simplified form, 1:5000. Ratios are frequently used in comparing quantities or scaling values.
Understanding ratios and proportions allows for solving problems involving scaling, such as: "If 10 out of 50000 people have a certain characteristic, how many people would have that characteristic in a population of 100,000?" This type of problem can be solved using proportional reasoning.
Advanced Concepts: Significant Figures and Rounding
In scientific and engineering contexts, the concept of significant figures becomes important. Significant figures are digits that carry meaning contributing to its measurement resolution. When working with decimals, it's often necessary to round the number to a specific number of significant figures to reflect the accuracy of the measurement or calculation. For instance, 0.0002 could be rounded to 0.0002 or, depending on the context, it might be more appropriate to express it in scientific notation as 2 x 10⁻⁴.
The choice of rounding depends on the level of precision required. In some applications, such as financial calculations, precision is paramount, and rounding might not be acceptable. In other cases, rounding might be necessary to simplify the results or to communicate the result more effectively.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve 10/50000? A: Yes, absolutely! Calculators are a valuable tool for solving fraction, decimal, and percentage conversions quickly and accurately.
-
Q: Why is simplifying a fraction important? A: Simplifying a fraction makes it easier to understand and work with. It reduces the numbers to their smallest equivalent form, making calculations simpler and reducing the chance of errors.
-
Q: What if I have a more complex fraction? A: The principles remain the same. Simplify the fraction if possible, then divide the numerator by the denominator to find the decimal equivalent. Multiply by 100 to find the percentage.
-
Q: How do I know how many significant figures to use? A: The number of significant figures used depends on the context of the calculation and the precision required. In scientific applications, guidelines regarding significant figures are usually provided.
-
Q: What other methods exist for converting fractions to decimals and percentages? A: Long division is a fundamental method for converting fractions to decimals. Other methods, especially for more complex fractions, may involve using mathematical properties or algorithms.
Conclusion: Mastering Numerical Relationships
Understanding the meaning and implications of 10/50000 goes beyond simply obtaining the answer 0.0002 or 0.02%. It's about grasping the fundamental concepts of fractions, decimals, percentages, and ratios. These are building blocks for more advanced mathematical understanding and are essential for navigating numerous aspects of life, from personal finance to scientific endeavors. By mastering these concepts, you equip yourself with tools for analyzing data, solving problems, and making informed decisions in a wide range of contexts. The seemingly simple question "What is 10/50000?" has thus served as a gateway to exploring a rich landscape of numerical relationships.
Latest Posts
Latest Posts
-
The Monster Book Of Monsters
Sep 16, 2025
-
What Is 45 Of 40
Sep 16, 2025
-
Coronoid Fossa Of The Humerus
Sep 16, 2025
-
Example Of An Information Text
Sep 16, 2025
-
Capitalize From In A Title
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 50000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.