What Is 10 Of 150000
marihuanalabs
Sep 13, 2025 · 5 min read
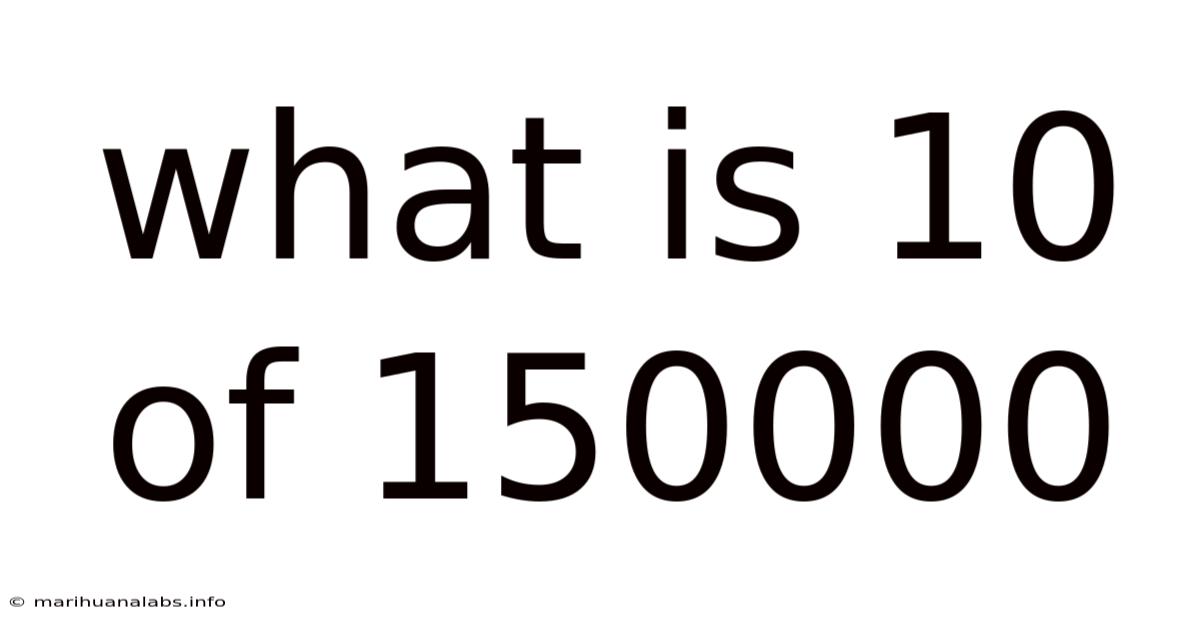
Table of Contents
What is 10/150000? Understanding Fractions, Percentages, and Proportions
This article explores the seemingly simple question: "What is 10/150000?" While the calculation itself is straightforward, delving into the topic unveils a wealth of mathematical concepts relevant to various fields, from everyday budgeting to complex scientific analyses. We’ll break down the calculation, explore different ways to represent the answer, and discuss the broader implications of understanding fractions, percentages, and proportions.
Understanding the Fraction 10/150000
The expression 10/150000 represents a fraction. In mathematics, a fraction signifies a part of a whole. The top number, 10, is the numerator, representing the part we are interested in. The bottom number, 150000, is the denominator, representing the total whole. This fraction indicates that we have 10 parts out of a total of 150000 parts.
To simplify this fraction and make it easier to understand, we need to find the greatest common divisor (GCD) of 10 and 150000. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. In this case, the GCD is 10. Dividing both the numerator and the denominator by 10, we get:
10 ÷ 10 = 1 150000 ÷ 10 = 15000
Therefore, the simplified fraction is 1/15000. This means that 10 out of 150000 is equivalent to 1 out of 15000. This simplified form is much more manageable for calculations and interpretations.
Calculating the Percentage
Expressing the fraction as a percentage provides a more intuitive understanding of its magnitude. To convert a fraction to a percentage, we multiply the fraction by 100%. So, for 1/15000:
(1/15000) * 100% = 0.006666...%
This can be rounded to approximately 0.007%. This signifies that 10 out of 150000 represents a very small proportion – less than one hundredth of a percent.
Decimal Representation
The fraction can also be represented as a decimal. To do this, we simply divide the numerator by the denominator:
1 ÷ 15000 = 0.00006666...
Again, this is a very small decimal number, highlighting the minute proportion represented by 10 out of 150000.
Practical Applications and Real-World Examples
Understanding how to calculate and interpret fractions, percentages, and proportions is crucial in many real-world scenarios:
-
Finance: Calculating interest rates, determining loan repayments, and understanding investment returns all rely on fractional and percentage calculations. Imagine a scenario where 150,000 represents the total number of shares in a company, and 10 shares are owned by an individual. The percentage ownership would be the same 0.007%, demonstrating a minimal stake in the company.
-
Science: In scientific experiments and data analysis, fractions and percentages are used extensively to represent proportions, ratios, and probabilities. For instance, in a clinical trial with 150,000 participants, if 10 experience a specific side effect, the percentage of participants experiencing that side effect would be 0.007%. This small percentage might still hold significant implications, depending on the severity of the side effect.
-
Surveys and Statistics: When analyzing survey data or conducting statistical analyses, fractions and percentages are fundamental for interpreting results and drawing conclusions. A survey of 150,000 people where only 10 respond in a particular way would show a very small percentage of respondents holding that specific opinion.
-
Everyday Life: From calculating discounts in a shop to determining the portion of a recipe, the concepts of fractions and percentages are applied constantly in our daily lives.
Proportion and Ratio
The relationship between 10 and 150000 can also be expressed as a ratio: 10:150000, or simplified to 1:15000. A ratio shows the relative size of two or more values. This ratio demonstrates that for every 15000 units of the whole, there is 1 unit of the part we are considering.
Expanding the Understanding: Working with Larger Numbers
While the initial problem might seem simple, working with larger numbers and more complex fractions reinforces the importance of simplifying and understanding the underlying mathematical principles. Imagine a scenario involving millions or billions of data points. The ability to simplify fractions and convert them into percentages or decimals becomes essential for effective data analysis and interpretation.
Furthermore, this exercise highlights the importance of numerical literacy. The ability to understand and work with fractions, percentages, and proportions is a valuable skill across various disciplines and everyday situations.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, absolutely. A calculator simplifies the division process, especially with larger numbers. However, understanding the underlying principles of fractions, percentages, and proportions remains crucial, even when using a calculator.
-
Q: What if the numerator was larger? A: If the numerator were larger, the resulting fraction, percentage, and decimal would be correspondingly larger. The principles remain the same; you would still simplify the fraction and convert it to a percentage or decimal to understand its magnitude.
-
Q: Are there different ways to represent this proportion? A: Yes, we've shown several: as a fraction (1/15000), a percentage (approximately 0.007%), and a decimal (approximately 0.00006666...). Each representation offers a slightly different perspective on the proportion.
-
Q: Why is simplification important? A: Simplification makes the fraction easier to understand and work with. It makes subsequent calculations less cumbersome and allows for a clearer interpretation of the data.
-
Q: What are some real-world applications beyond those mentioned? A: Numerous fields, including engineering, computer science, economics, and social sciences rely heavily on fractional and percentage calculations for modeling, analysis, and interpretation of data.
Conclusion
The seemingly straightforward question, "What is 10/150000?", opens a door to a deeper understanding of fundamental mathematical concepts. By exploring the fraction, percentage, decimal, and ratio representations, we've illustrated the importance of numerical literacy and its relevance to various aspects of life. The ability to work confidently with fractions and proportions is a transferable skill that empowers individuals to interpret data, solve problems, and make informed decisions in diverse contexts. Remember that even seemingly small proportions, like 0.007%, can have significant implications depending on the context and scale of the situation. Understanding how to work with these proportions is a key skill for anyone aiming for numerical fluency.
Latest Posts
Latest Posts
-
Author Of The Faerie Queene
Sep 13, 2025
-
Types Of Observation In Psychology
Sep 13, 2025
-
Verb Endings Spanish Present Tense
Sep 13, 2025
-
Timothy Dalton In Jane Eyre
Sep 13, 2025
-
What Is A Petrarchan Lover
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 150000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.