What Is 10 Of 150
marihuanalabs
Sep 16, 2025 · 5 min read
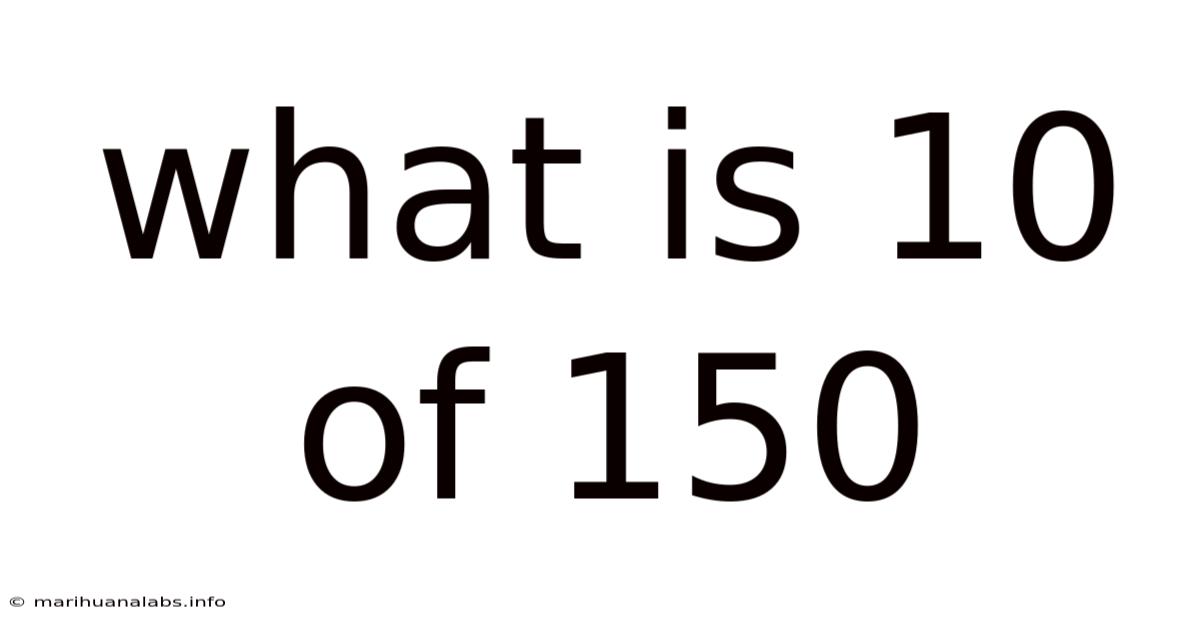
Table of Contents
What is 10/150? Understanding Fractions, Percentages, and Decimals
This article will explore the question "What is 10/150?" in a comprehensive way, going beyond a simple numerical answer to provide a deeper understanding of fractions, percentages, and decimals. We'll cover how to simplify fractions, convert them to percentages and decimals, and delve into the practical applications of this type of calculation in everyday life. Understanding these concepts is crucial for various fields, from basic arithmetic to advanced mathematics, finance, and more.
Introduction: Understanding Fractions
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In the fraction 10/150, 10 is the numerator and 150 is the denominator. This means we are considering 10 parts out of a total of 150 parts.
Simplifying the Fraction: Finding the Greatest Common Divisor (GCD)
Before converting 10/150 to a percentage or decimal, it's essential to simplify the fraction to its lowest terms. This makes the fraction easier to understand and work with. Simplifying involves dividing both the numerator and denominator by their greatest common divisor (GCD). The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In this case, the GCD of 10 and 150 is 10. Therefore, we divide both the numerator and the denominator by 10:
10 ÷ 10 = 1 150 ÷ 10 = 15
So, the simplified fraction is 1/15. This means that 10/150 and 1/15 represent the same value. They are equivalent fractions.
Converting the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In the case of 1/15:
1 ÷ 15 ≈ 0.066666...
The result is a repeating decimal. We can round this to a certain number of decimal places for practical purposes. For example, rounded to two decimal places, it's 0.07. Rounded to three decimal places, it's 0.067. The choice of rounding depends on the level of precision required.
Converting the Fraction to a Percentage
A percentage represents a fraction out of 100. To convert a fraction to a percentage, we first convert it to a decimal, and then multiply by 100 and add the "%" symbol.
Using our simplified fraction 1/15 and its decimal equivalent of approximately 0.066666..., we can calculate the percentage:
0.066666... × 100 ≈ 6.6666...%
Again, we can round this to a certain number of decimal places. Rounded to two decimal places, it's 6.67%. Rounded to one decimal place, it's 6.7%.
Practical Applications and Real-World Examples
Understanding how to work with fractions, decimals, and percentages is vital in numerous real-world scenarios:
-
Calculating Discounts: Imagine a store offering a 10% discount on an item priced at $150. To find the discount amount, you'd calculate 10% of $150, which is the same as finding 10/150 of $150. This is equivalent to $15 (10/150 * $150 = $15).
-
Determining Proportions: If a survey shows that 10 out of 150 respondents prefer a particular product, this can be expressed as the fraction 10/150 or the simplified fraction 1/15. This helps understand the proportion of respondents who prefer that product.
-
Understanding Financial Statements: Financial reports often use fractions and percentages to represent key metrics like profit margins, debt-to-equity ratios, and return on investment. Being able to interpret these figures is essential for making informed financial decisions.
-
Baking and Cooking: Many recipes use fractions to specify ingredient quantities (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt). Converting these fractions to decimals or percentages can be helpful depending on the measuring tools available.
-
Science and Engineering: Fractions and decimals are fundamental to many scientific and engineering calculations, from calculating the ratio of ingredients in a chemical mixture to determining the dimensions of a structure.
Further Exploration: Working with More Complex Fractions
While 10/150 is a relatively simple fraction, the principles discussed here apply to more complex fractions as well. The key steps remain the same:
- Simplify the fraction: Find the greatest common divisor (GCD) of the numerator and denominator and divide both by it.
- Convert to a decimal: Divide the numerator by the denominator.
- Convert to a percentage: Multiply the decimal equivalent by 100.
Frequently Asked Questions (FAQ)
-
Q: Is it always necessary to simplify a fraction? A: While not always strictly necessary, simplifying a fraction makes it easier to work with and understand. It reduces the risk of errors in further calculations.
-
Q: How do I find the GCD of larger numbers? A: There are several methods for finding the GCD, including the Euclidean algorithm. Many calculators and computer programs can also calculate the GCD automatically.
-
Q: What if the decimal representation of a fraction is non-repeating and non-terminating? A: Some fractions, when converted to decimals, result in infinite non-repeating decimal expansions (like pi). In such cases, you would typically round the decimal to a suitable number of places depending on the context and the required level of accuracy.
-
Q: Are there any other ways to express 10/150? A: Yes, besides decimal and percentage, you could express it as a ratio (1:15), or even in a word problem format such as "10 out of 150".
Conclusion: Mastering Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill applicable across various disciplines. This article has shown how to handle the specific fraction 10/150, demonstrating the process of simplification, decimal conversion, and percentage calculation. By mastering these concepts, you build a strong foundation for more advanced mathematical and practical applications in your daily life and future studies. Remember that practice is key; the more you work with these concepts, the more comfortable and confident you'll become. Don't hesitate to explore further examples and practice problems to solidify your understanding.
Latest Posts
Latest Posts
-
Dance Dance Dance Dance Lyrics
Sep 16, 2025
-
Is Sulfur A Diatomic Molecule
Sep 16, 2025
-
What Is 10 Of 300000
Sep 16, 2025
-
Words That Describe A Beach
Sep 16, 2025
-
The Last Judgement Chancery Lane
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.