What Is 10 Of 15
marihuanalabs
Sep 09, 2025 · 5 min read
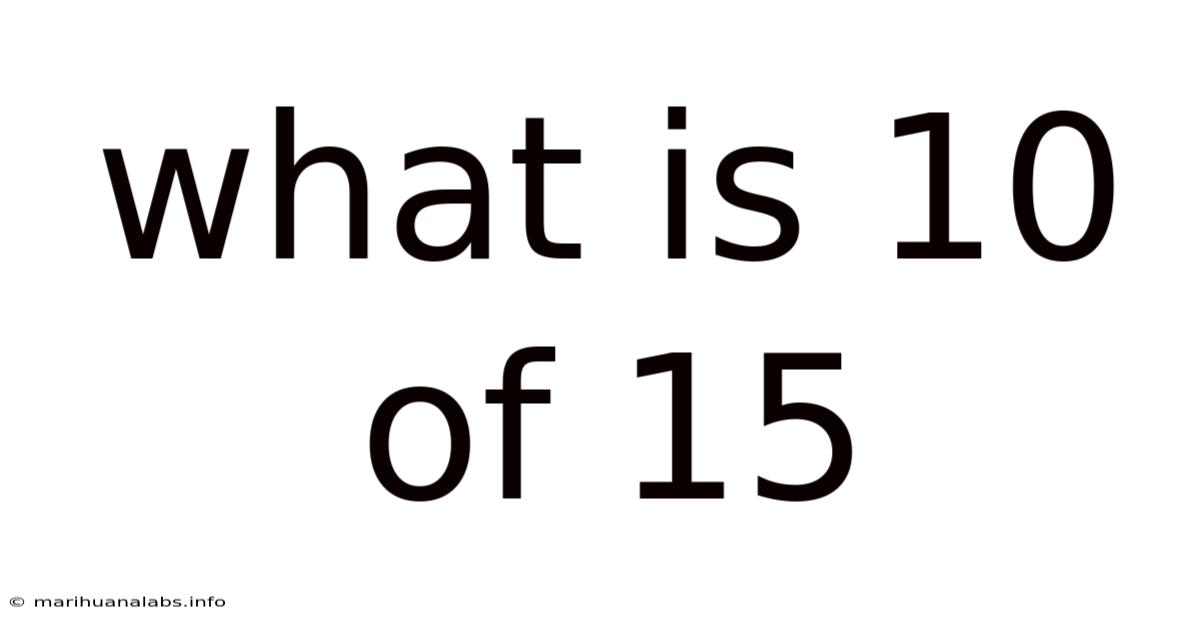
Table of Contents
What is 10 out of 15? Understanding Fractions, Percentages, and Ratios
What is 10 out of 15? This seemingly simple question opens the door to a deeper understanding of fundamental mathematical concepts: fractions, percentages, and ratios. While the immediate answer might seem obvious to some, exploring the various ways to represent and interpret this relationship provides valuable insights into proportional reasoning and its applications in everyday life. This article will delve into the calculation, different representations, and real-world examples of this seemingly simple mathematical problem.
Understanding the Basics: Fractions, Ratios, and Percentages
Before tackling "10 out of 15," let's establish a firm grasp on the core concepts involved.
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, and the denominator indicates the total number of parts in the whole. In our case, "10 out of 15" can be directly expressed as the fraction 10/15.
Ratios: A ratio compares two or more quantities. It shows the relative sizes of the quantities. "10 out of 15" can be expressed as a ratio of 10:15 (read as "10 to 15"). Ratios can be simplified just like fractions.
Percentages: A percentage represents a fraction of 100. It expresses a proportion as a number out of 100. To convert a fraction to a percentage, you multiply the fraction by 100%.
Calculating 10 out of 15: The Step-by-Step Approach
-
Express as a Fraction: The phrase "10 out of 15" translates directly to the fraction 10/15.
-
Simplify the Fraction: We can simplify this fraction by finding the greatest common divisor (GCD) of the numerator (10) and the denominator (15). The GCD of 10 and 15 is 5. Dividing both the numerator and the denominator by 5 gives us:
10/15 = (10 ÷ 5) / (15 ÷ 5) = 2/3
-
Convert to a Percentage: To express 2/3 as a percentage, we multiply it by 100%:
(2/3) * 100% ≈ 66.67%
-
Express as a Decimal: Dividing the numerator by the denominator gives us the decimal representation:
2 ÷ 3 ≈ 0.6667
Therefore, 10 out of 15 is equivalent to 2/3, 66.67%, and approximately 0.6667.
Real-World Applications: Understanding Proportions in Context
Understanding "10 out of 15" isn't just about manipulating numbers; it's about grasping proportions and applying them to real-world situations. Let's explore some examples:
-
Test Scores: If you answered 10 questions correctly out of 15 on a test, your score would be 66.67%. This helps you understand your performance relative to the total number of questions.
-
Surveys and Statistics: Imagine a survey where 10 out of 15 respondents preferred a particular product. This represents 66.67% preference, a crucial piece of information for market analysis.
-
Recipe Scaling: If a recipe calls for 15 units of an ingredient and you only want to make 2/3 of the recipe, you would use 10 units (2/3 * 15 = 10).
-
Geometry and Measurement: If a line segment is 15 units long, and a smaller segment within it measures 10 units, then the smaller segment represents 2/3 of the total length.
-
Financial Calculations: If you invested $15 and earned a profit of $10, your return on investment would be 66.67%.
Beyond the Basics: Exploring Deeper Mathematical Concepts
The seemingly simple calculation of "10 out of 15" provides a foundation for understanding more complex mathematical ideas:
-
Probability: If you randomly select one item from a set of 15 items, the probability of selecting a specific item from a group of 10 similar items is 10/15, or 2/3.
-
Proportional Reasoning: This is a critical skill used in solving problems involving proportions and ratios. Understanding "10 out of 15" helps develop this crucial skill.
-
Algebra: Problems involving proportions often translate into algebraic equations. For example, if x is 2/3 of 15, we can write the equation x = (2/3) * 15, which simplifies to x = 10.
-
Advanced Statistics: Concepts like relative frequency and conditional probability build upon the understanding of fractions and ratios.
Frequently Asked Questions (FAQs)
Q: Can I express 10 out of 15 as a different fraction?
A: Yes, 2/3 is the simplest form, but equivalent fractions exist, such as 4/6, 6/9, 8/12, etc. All these fractions represent the same proportion.
Q: Why is simplification important?
A: Simplifying fractions makes them easier to understand and work with. It presents the proportion in its most concise and manageable form.
Q: What if I have a more complex ratio, say, 25 out of 40?
A: You would follow the same steps: express it as a fraction (25/40), simplify it (5/8), and then convert it to a percentage (approximately 62.5%) or a decimal (0.625).
Q: How accurate does the percentage need to be?
A: The level of accuracy depends on the context. For many applications, rounding to one or two decimal places is sufficient (e.g., 66.67%). In scientific or engineering contexts, more precision might be needed.
Conclusion: The Significance of Understanding Proportions
The seemingly simple question "What is 10 out of 15?" provides a gateway to understanding fundamental mathematical concepts with broad applications. By exploring fractions, percentages, ratios, and their real-world implications, we develop critical thinking skills essential for various fields, from everyday problem-solving to advanced scientific analysis. The ability to understand and manipulate proportions is a cornerstone of mathematical literacy and is crucial for navigating the complexities of the world around us. Mastering these concepts opens doors to a deeper appreciation of the power of mathematics in everyday life. Remember, the journey of understanding mathematics is a continuous process of exploration and application. Each seemingly simple problem, like "10 out of 15," holds the potential to unlock a deeper understanding of the mathematical world.
Latest Posts
Latest Posts
-
Sword In The Stone Squirrel
Sep 09, 2025
-
Age Of Sexual Consent Illinois
Sep 09, 2025
-
Convert Fl Ounces To Ml
Sep 09, 2025
-
Reactions Of Metals With Acids
Sep 09, 2025
-
What Is 2 3kg In Pounds
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.