What Is 10 Of 1000
marihuanalabs
Sep 06, 2025 · 6 min read
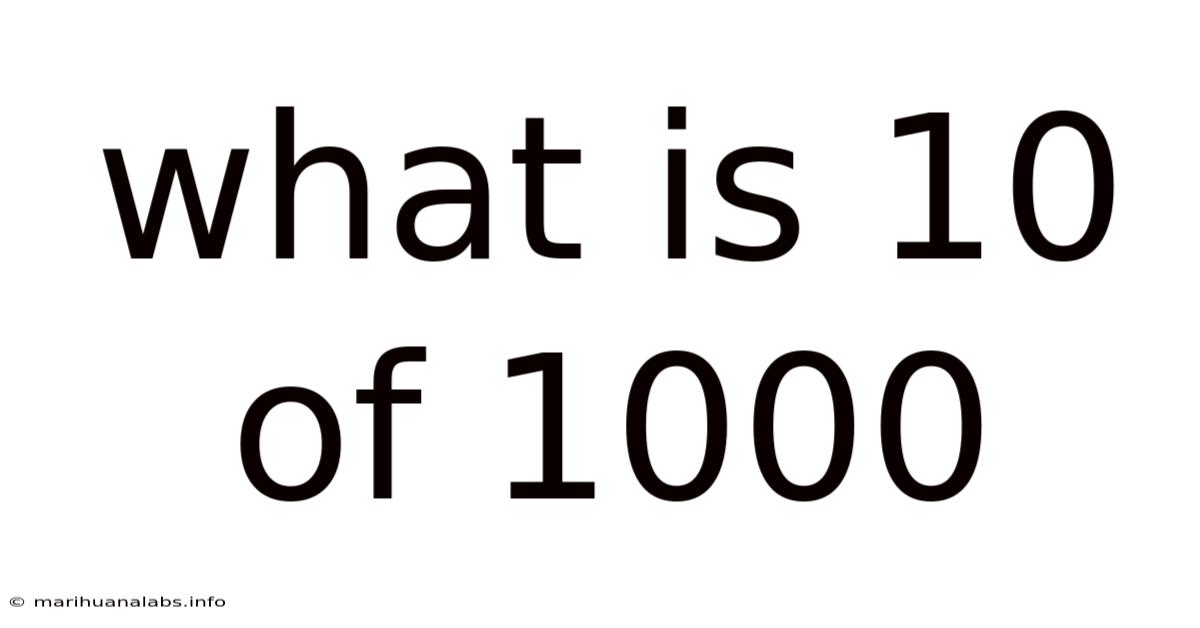
Table of Contents
What is 10/1000? Understanding Fractions, Decimals, and Percentages
What is 10/1000? This seemingly simple question opens a door to a fundamental understanding of fractions, decimals, and percentages – concepts crucial in various aspects of life, from everyday finances to advanced scientific calculations. This article will delve deep into understanding 10/1000, exploring its various representations and applications, providing a comprehensive guide for learners of all levels.
Introduction: Fractions as a Foundation
The expression "10/1000" represents a fraction. In mathematics, a fraction signifies a part of a whole. The number on top, the 10, is called the numerator, indicating the number of parts we're considering. The number on the bottom, the 1000, is called the denominator, representing the total number of equal parts the whole is divided into. Therefore, 10/1000 means 10 parts out of a total of 1000 equal parts.
Understanding fractions is foundational to grasping decimals and percentages. They are all different ways of expressing the same numerical value, offering varying perspectives and levels of detail.
Simplifying Fractions: Finding the Essence
Before exploring other representations, let's simplify the fraction 10/1000. Simplifying a fraction means reducing it to its simplest form, where the numerator and denominator have no common factors other than 1. Both 10 and 1000 are divisible by 10:
10 ÷ 10 = 1 1000 ÷ 10 = 100
Therefore, 10/1000 simplifies to 1/100. This simplified form retains the same value as the original fraction but is more concise and easier to work with.
Converting to Decimals: Unveiling the Decimal Representation
Fractions can be easily converted into decimals by performing the division indicated by the fraction bar. In this case, we divide the numerator (1) by the denominator (100):
1 ÷ 100 = 0.01
Thus, 10/1000 (or its simplified form, 1/100) is equal to 0.01 as a decimal. The decimal representation provides a more straightforward way to visualize the numerical value, especially when dealing with calculations involving other decimals.
Understanding the Place Value System
The decimal representation 0.01 highlights the importance of the place value system. The digit 1 is in the hundredths place, meaning it represents one-hundredth of a whole. This reinforces the understanding that 1/100 (or 10/1000) represents a small portion of a whole. Understanding place value is crucial for accurately interpreting and manipulating decimal numbers.
Converting to Percentages: Expressing Proportion in a Different Light
Percentages express a fraction or decimal as a proportion of 100. To convert a decimal to a percentage, simply multiply by 100 and add the percent symbol (%).
0.01 × 100 = 1%
Therefore, 10/1000 is equivalent to 1%. The percentage representation is particularly useful for comparing proportions and expressing relative values, often used in areas like finance, statistics, and probability.
Real-World Applications: Where does 10/1000 Appear?
Understanding 10/1000, its decimal (0.01), and percentage (1%) equivalents extends beyond theoretical mathematics. Here are a few real-world examples showcasing its application:
-
Finance: Imagine having a savings account with $1000. If you earn 1% interest, you would gain $10 (1% of $1000). This demonstrates the direct application of the percentage form.
-
Statistics: If you conduct a survey of 1000 people and 10 respond positively to a particular question, the response rate is 1%. This showcases the direct applicability of the fraction and percentage.
-
Measurement: If you are measuring a length of 1000 millimeters and a section measures 10 millimeters, that section represents 1% of the total length. This highlights the fraction and percentage form's relevance in measurement sciences.
-
Science: In scientific experiments involving dilutions or concentrations, expressing a ratio as a fraction, decimal, or percentage is crucial for accurate reporting and repeatability. A concentration of 0.01M (molar) is directly related to our example.
-
Probability: In probabilistic scenarios, 1% might represent the probability of a specific event occurring among 1000 possible outcomes.
Explaining 10/1000 to Children: A Simple Approach
Explaining 10/1000 to children requires a simplified, relatable approach. Visual aids like diagrams or objects are incredibly helpful.
-
Use Objects: Take 1000 small objects (e.g., beads or candies). Set aside 10 of them. Explain that the 1000 represents the whole, and the 10 represents the part you are focusing on.
-
Use a Pizza: Imagine a pizza cut into 1000 slices. Taking 10 slices represents 10/1000 of the pizza.
-
Relate to Familiar Concepts: Connect it to percentages they might already understand. For example, 1% is a very small amount, like getting one candy out of a bag of 100 candies.
-
Focus on Simplification: Show them that 10/1000 simplifies to 1/100, making it easier to understand.
-
Use Interactive Games: Games and activities can make learning fractions, decimals, and percentages fun and engaging.
Advanced Concepts and Further Exploration
Beyond the basic understanding, exploring advanced concepts related to fractions, decimals, and percentages can deepen one's mathematical comprehension:
-
Ratio and Proportion: Understanding how 10/1000 represents a ratio of 10 to 1000 and how this relates to proportions within larger datasets.
-
Scientific Notation: Representing extremely large or small numbers using scientific notation can streamline calculations involving fractions and decimals.
-
Significant Figures: Understanding significant figures is crucial when working with decimal numbers representing measurements or experimental data, ensuring accuracy and precision in results.
Frequently Asked Questions (FAQ)
-
Q: Can 10/1000 be expressed in other ways? A: Yes, it can be expressed as a simplified fraction (1/100), a decimal (0.01), and a percentage (1%).
-
Q: What is the difference between a fraction and a decimal? A: A fraction represents a part of a whole using a numerator and a denominator, while a decimal uses a base-ten system to represent the same value.
-
Q: How do I convert a fraction to a percentage? A: Divide the numerator by the denominator to get a decimal, then multiply the decimal by 100 and add the % symbol.
-
Q: Why is simplifying fractions important? A: Simplifying fractions makes them easier to understand, compare, and use in calculations.
-
Q: What are some real-life examples where I might encounter 10/1000? A: Many areas, including finance, statistics, science, and measurement, utilize this concept.
Conclusion: Mastering the Fundamentals
Understanding 10/1000 is more than just knowing its numerical value. It’s about grasping the fundamental principles of fractions, decimals, and percentages – tools essential for navigating various aspects of life and further mathematical learning. By grasping these concepts, and applying them through practical examples, one develops a solid foundation for more complex mathematical endeavors. The ability to confidently convert between fractions, decimals, and percentages opens doors to greater comprehension and proficiency in numerous fields. Remember, consistent practice and a curious mindset are key to mastering these fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Member Of King Arthurs Court
Sep 07, 2025
-
1 Million Days In Years
Sep 07, 2025
-
Shoot For The Stars Tattoo
Sep 07, 2025
-
Safe Travels In German Language
Sep 07, 2025
-
Catcher And The Rye Characters
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.