What Is 10 Of 100
marihuanalabs
Sep 06, 2025 · 6 min read
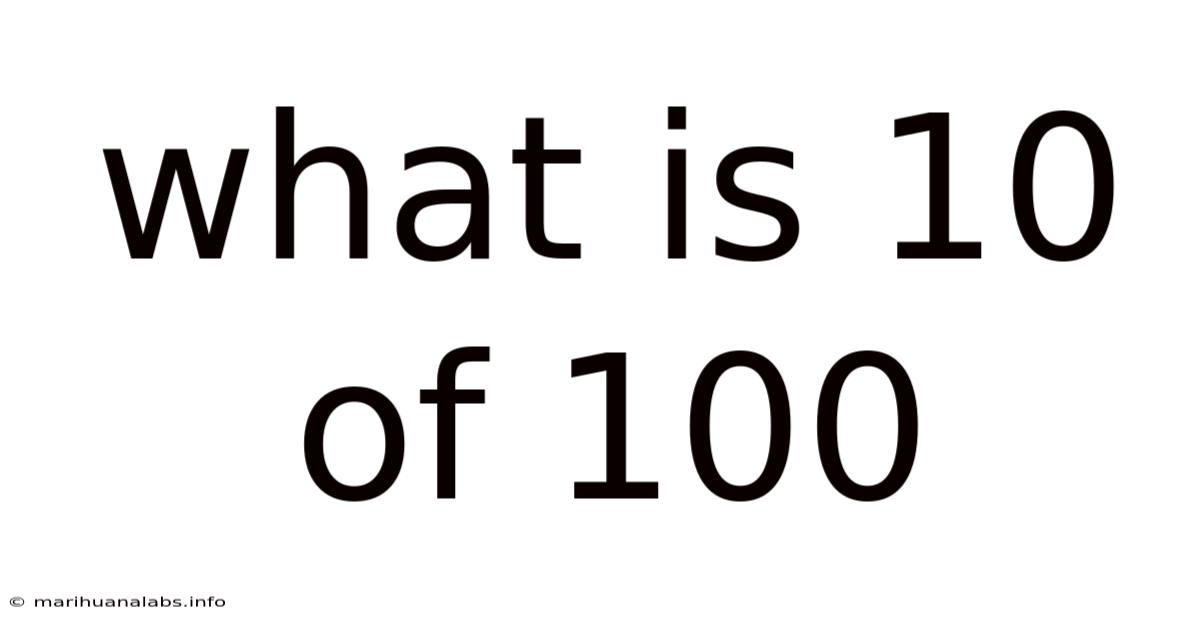
Table of Contents
What is 10 of 100? Understanding Fractions, Percentages, and Ratios
Understanding the relationship between numbers is fundamental to mathematics and everyday life. This article delves into the seemingly simple question, "What is 10 of 100?", exploring its representation as a fraction, percentage, and ratio, and explaining the underlying mathematical concepts. We'll go beyond the basic answer to build a solid understanding of these interconnected concepts.
Introduction: Deconstructing "10 of 100"
The phrase "10 of 100" inherently implies a part-to-whole relationship. We have a smaller quantity (10) that is a component of a larger quantity (100). This simple statement forms the basis for understanding fractions, percentages, and ratios, all crucial tools for analyzing proportions and solving various mathematical problems. We will explore these different mathematical representations and their practical applications.
1. Representing "10 of 100" as a Fraction
A fraction is a numerical representation of a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The numerator represents the part, and the denominator represents the whole.
In our case, "10 of 100" can be directly represented as the fraction 10/100. This fraction signifies that 10 is one part of a whole consisting of 100 parts.
Simplifying Fractions: Fractions can often be simplified by finding the greatest common divisor (GCD) of both the numerator and the denominator and dividing both by that number. The GCD of 10 and 100 is 10. Therefore, 10/100 simplifies to 1/10. This means that 10 out of 100 is equivalent to 1 out of 10. Both fractions represent the same proportion.
Understanding Fraction Equivalence: It's important to grasp that 10/100 and 1/10 represent the same value. They are equivalent fractions. Simplifying fractions makes them easier to work with and understand the magnitude of the proportion.
2. Expressing "10 of 100" as a Percentage
A percentage is a way of expressing a fraction as a proportion of 100. The word "percent" literally means "out of one hundred" ( per cent). To convert a fraction to a percentage, we multiply the fraction by 100%.
In our example, 10/100 * 100% = 10%. This means that "10 of 100" is equivalent to 10 percent. This is a common and easily understood way of expressing proportions.
Practical Applications of Percentages: Percentages are extensively used in various contexts:
- Discounts and Sales: A 10% discount on a product means you save 10% of the original price.
- Financial Calculations: Interest rates, tax rates, and investment returns are typically expressed as percentages.
- Data Representation: Charts and graphs frequently utilize percentages to visualize proportions within datasets.
- Academic Grades: Many grading systems use percentages to represent student performance.
3. Representing "10 of 100" as a Ratio
A ratio is a comparison of two quantities. It shows the relative size of one quantity to another. Ratios can be expressed in several ways: using a colon (:), as a fraction, or using the word "to".
"10 of 100" can be expressed as a ratio as 10:100 or 10 to 100. This indicates a comparison of 10 to 100. Similar to fractions, ratios can also be simplified. The simplified ratio is 1:10.
Different Types of Ratios:
- Part-to-Part Ratio: Compares one part of a whole to another part. Example: If there are 10 boys and 20 girls in a class, the boy-to-girl ratio is 10:20 or 1:2.
- Part-to-Whole Ratio: Compares one part of a whole to the whole itself. Our example, 10:100, is a part-to-whole ratio.
Applications of Ratios: Ratios are fundamental in many fields, including:
- Scaling and Proportion: Used in blueprints, maps, and recipes.
- Mixing Ingredients: In cooking or chemistry, ratios specify the proportions of different components.
- Financial Analysis: Comparing different financial metrics, like debt-to-equity ratios.
Mathematical Operations with Fractions, Percentages, and Ratios
Understanding "10 of 100" allows us to extend our knowledge to other mathematical operations involving fractions, percentages, and ratios.
1. Finding a Percentage of a Number: If we want to find 10% of any number, we multiply the number by 0.10 (which is the decimal equivalent of 10%). For example, 10% of 500 is 500 * 0.10 = 50.
2. Converting between Fractions, Percentages, and Decimals: These three are interchangeable. To convert a fraction to a decimal, divide the numerator by the denominator. To convert a decimal to a percentage, multiply by 100%. To convert a percentage to a decimal, divide by 100%.
3. Solving Proportion Problems: Problems involving proportions often involve setting up an equation with equivalent ratios. For example, if 10 out of 100 apples are bad, how many bad apples would you expect in a batch of 500 apples? We can set up a proportion: 10/100 = x/500. Solving for x, we get x = 50 bad apples.
Beyond the Basics: Exploring Advanced Concepts
The simple concept of "10 of 100" opens doors to more complex mathematical ideas:
- Probability: The probability of an event occurring can be expressed as a fraction, percentage, or ratio. If there's a 10% chance of rain, the probability of rain is 10/100 or 1/10.
- Statistics: Understanding proportions is crucial for analyzing data, calculating averages, and understanding statistical distributions.
- Algebra: Proportions are frequently used in algebraic equations and problem-solving.
Frequently Asked Questions (FAQ)
Q1: What's the difference between a fraction and a ratio?
A1: While both compare quantities, fractions represent a part of a whole, while ratios compare two quantities, which may or may not be parts of a whole.
Q2: Can I express "10 of 100" in other ways?
A2: Yes, you can also express it as 0.1 (decimal), 1/10 (simplified fraction), 1:10 (simplified ratio), or one-tenth.
Q3: How can I use this knowledge in real-life situations?
A3: Understanding fractions, percentages, and ratios is essential for budgeting, shopping (calculating discounts), understanding statistics, and many other daily tasks.
Q4: What if the numbers aren't as easily simplified?
A4: If the numerator and denominator don't share a common factor, you can still express the fraction as a decimal or a percentage, and you can always use a calculator to find the decimal representation.
Q5: Why is it important to simplify fractions and ratios?
A5: Simplifying makes them easier to understand and compare. It's also crucial for performing calculations more efficiently.
Conclusion: The Significance of Understanding Proportions
The seemingly simple question, "What is 10 of 100?", has led us on a journey through the fundamental concepts of fractions, percentages, and ratios. These are interconnected mathematical tools that are essential for comprehending proportions and solving a vast array of problems in various fields. Mastering these concepts provides a solid foundation for further mathematical exploration and real-world application, enabling you to analyze data, solve problems, and make informed decisions in your daily life. The understanding of "10 of 100" is not just about a numerical answer but a gateway to understanding the language of proportions in mathematics.
Latest Posts
Latest Posts
-
Capital Cities In Middle East
Sep 07, 2025
-
What Is A Mitigating Factor
Sep 07, 2025
-
Gross Weight Vs Net Weight
Sep 07, 2025
-
A Gross Is How Many
Sep 07, 2025
-
Define Much Ado About Nothing
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.