What Is 1/2 Of 1
marihuanalabs
Sep 07, 2025 · 6 min read
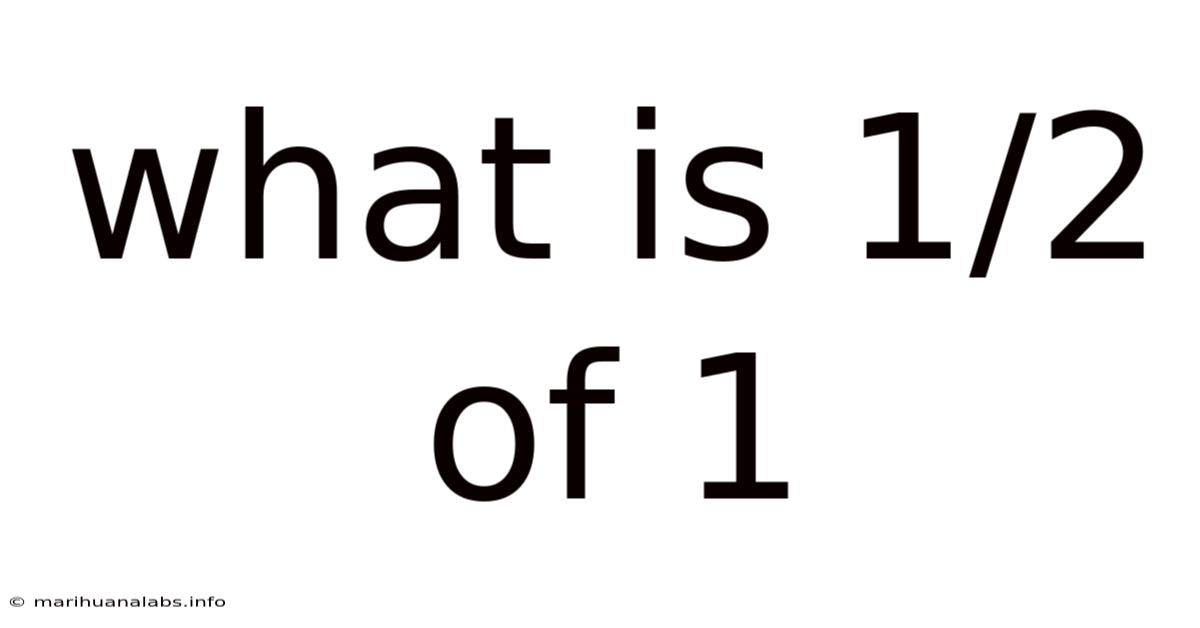
Table of Contents
What is 1/2 of 1? Unpacking Fractions and Their Applications
This seemingly simple question, "What is 1/2 of 1?", opens a door to a vast world of mathematical concepts, crucial for understanding fractions, proportions, and various real-world applications. While the answer might seem immediately obvious to many, a deeper exploration reveals the underlying principles and provides a solid foundation for more complex mathematical operations. This article will guide you through the process of understanding this basic fraction problem, explaining the logic behind the calculation, and expanding on its implications in various fields.
Understanding Fractions: Building Blocks of Mathematics
Before diving into the calculation, let's establish a clear understanding of what a fraction represents. A fraction, in its simplest form, is a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
In the fraction 1/2, the denominator (2) signifies that the whole is divided into two equal parts. The numerator (1) indicates that we're considering one of those two parts. This simple representation allows us to express portions, ratios, and proportions in a precise and quantifiable manner.
Calculating 1/2 of 1: A Step-by-Step Approach
To calculate 1/2 of 1, we simply multiply the fraction (1/2) by the whole number (1):
(1/2) x 1 = 1/2
This calculation demonstrates that half (1/2) of one whole unit is indeed one-half (1/2). This might seem trivial, but understanding the multiplication process with fractions is fundamental. When multiplying a fraction by a whole number, we essentially multiply the numerator by the whole number and keep the denominator the same.
Visualizing the Concept: A Practical Representation
Imagine a single pizza (representing our whole, which is 1). To find 1/2 of the pizza, we cut the pizza into two equal slices. Taking one of those slices means we have 1/2 of the pizza. This visual representation clearly demonstrates the concept of a fraction and the result of the calculation.
Extending the Concept: Beyond 1/2 of 1
This basic understanding forms the foundation for more complex fraction problems. Let's explore some variations:
- 1/2 of any whole number: To find 1/2 of any whole number, simply divide the whole number by 2. For example, 1/2 of 10 is 10/2 = 5.
- Other fractions of 1: The same principle applies to other fractions. For instance, 1/3 of 1 is 1/3; 1/4 of 1 is 1/4, and so on. This illustrates that any fraction of 1 is simply that fraction itself.
- Fractions of fractions: This involves multiplying two fractions. For example, to find 1/2 of 1/4, we multiply the numerators and the denominators: (1/2) x (1/4) = 1/8. This shows how fractions can be used to represent increasingly smaller portions of a whole.
Real-World Applications: Fractions in Everyday Life
Fractions are not just abstract mathematical concepts; they have significant practical applications in numerous aspects of our daily lives:
- Cooking and Baking: Recipes frequently use fractions (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt). Accurate measurements are crucial for successful cooking.
- Measurement: We use fractions in various measurement systems (e.g., inches, centimeters, feet). Understanding fractions ensures precise measurements in construction, engineering, and other fields.
- Finance: Fractions are used extensively in finance for calculating percentages, interest rates, and proportions of investments.
- Data Analysis: Fractions and proportions are indispensable for analyzing data and drawing conclusions in research, statistics, and scientific studies.
- Geometry and Trigonometry: Many geometrical concepts and trigonometric functions utilize fractions for expressing ratios, proportions, and angles.
The Importance of Understanding Fractions
Mastering the concept of fractions is fundamental for success in mathematics and beyond. It's a gateway to more advanced mathematical concepts like decimals, percentages, ratios, and proportions. A strong grasp of fractions is essential for understanding various subjects, including science, engineering, finance, and even everyday problem-solving.
Beyond the Basics: Decimals and Percentages
Fractions, decimals, and percentages are all different ways of representing the same thing: parts of a whole. They are interconnected and can be easily converted from one form to another.
- Converting fractions to decimals: To convert a fraction to a decimal, simply divide the numerator by the denominator. For example, 1/2 = 1 ÷ 2 = 0.5.
- Converting fractions to percentages: To convert a fraction to a percentage, multiply the fraction by 100%. For example, 1/2 x 100% = 50%.
- Converting decimals and percentages to fractions: The reverse process is equally important and requires understanding place value and the relationship between fractions, decimals, and percentages.
Frequently Asked Questions (FAQ)
Q1: What is the difference between 1/2 and 0.5?
A1: 1/2 and 0.5 are equivalent representations of the same value. 1/2 is the fractional representation, while 0.5 is the decimal representation.
Q2: Can I use a calculator to find 1/2 of 1?
A2: While a calculator is not necessary for this specific calculation, it's a useful tool for solving more complex fraction problems.
Q3: Why is understanding fractions important for advanced mathematics?
A3: Fractions form the building blocks for many advanced mathematical concepts. Understanding fractions is crucial for working with algebra, calculus, and other higher-level mathematics.
Q4: Are there any real-world examples of fractions beyond what you mentioned?
A4: Yes! Think about sharing something equally among friends (splitting a pizza, sharing candy), determining the amount of ingredients needed for a recipe scaled to different sizes, or calculating discounts and sales tax. Fractions are everywhere!
Q5: How can I improve my skills in working with fractions?
A5: Practice is key! Start with simple calculations, gradually working your way up to more complex problems. Use visual aids like diagrams and real-world objects to help you understand the concepts. There are also numerous online resources and educational materials that can help you improve your fraction skills.
Conclusion: Embracing the Power of Fractions
The seemingly simple question, "What is 1/2 of 1?", has led us on a journey through the world of fractions. We've explored the underlying principles, visualized the concept, and examined its numerous applications. Understanding fractions is not just about memorizing formulas; it's about developing a deep understanding of how to represent and manipulate parts of a whole. This knowledge serves as a crucial foundation for future mathematical endeavors and helps us navigate the quantitative aspects of our everyday lives. By mastering fractions, we unlock a powerful tool for solving problems, understanding data, and engaging with the world around us in a more informed and insightful way. So, embrace the power of fractions and unlock your mathematical potential!
Latest Posts
Latest Posts
-
Descriptive Linguistics Vs Prescriptive Linguistics
Sep 08, 2025
-
What Do Elves Look Like
Sep 08, 2025
-
Definition Of Murder By Law
Sep 08, 2025
-
What Is 4 Of 50000
Sep 08, 2025
-
What Is 30 Of 70
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.