What Is 1/2 + 2/3
marihuanalabs
Sep 20, 2025 · 5 min read
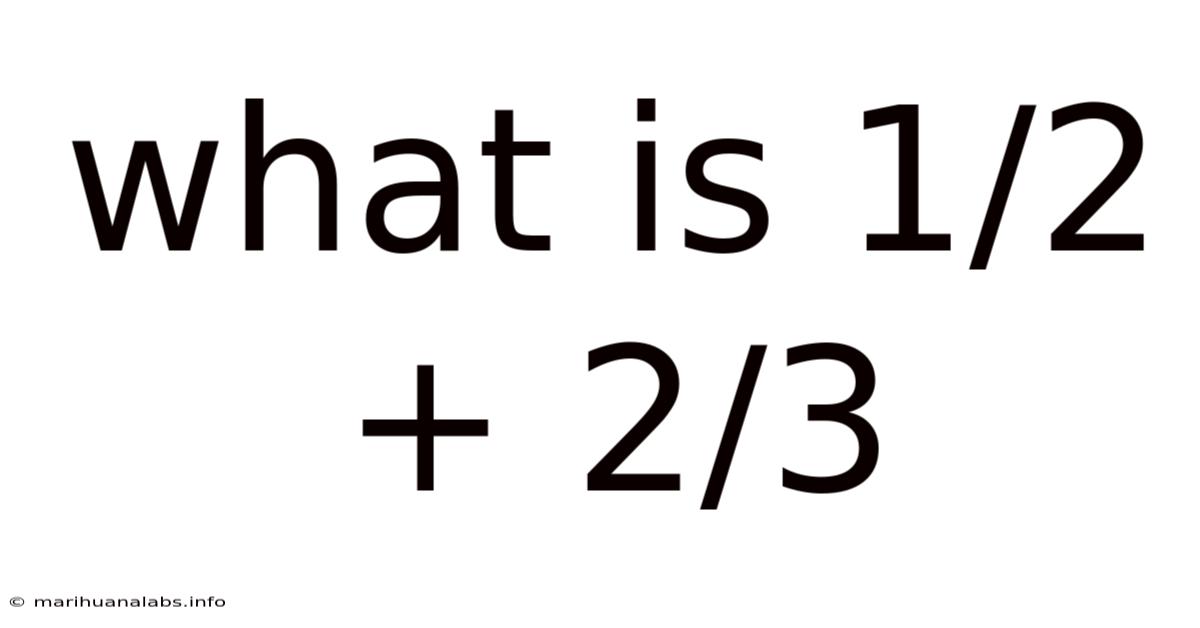
Table of Contents
What is 1/2 + 2/3? A Deep Dive into Fraction Addition
This article explores the seemingly simple yet fundamentally important mathematical operation of adding fractions: specifically, what is the sum of 1/2 and 2/3? We'll move beyond simply providing the answer, delving into the underlying principles, providing step-by-step guidance, and exploring the broader context of fraction arithmetic. This comprehensive guide is designed for anyone, from elementary school students brushing up on their fractions to adults looking to refresh their mathematical skills.
Understanding Fractions: A Quick Refresher
Before tackling the addition problem, let's establish a firm understanding of fractions themselves. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/2 (one-half), the numerator is 1 (we have one part), and the denominator is 2 (the whole is divided into two equal parts). Similarly, in 2/3 (two-thirds), the numerator is 2, and the denominator is 3.
Why Can't We Simply Add Numerators and Denominators?
A common mistake when adding fractions is to simply add the numerators and the denominators. For instance, incorrectly adding 1/2 + 2/3 as (1+2)/(2+3) = 3/5 is a fundamental error. This approach doesn't accurately represent the proportional parts being combined. Think of it like trying to add apples and oranges directly – you can't do it without considering a common unit of measurement.
Finding a Common Denominator: The Key to Fraction Addition
To correctly add fractions, we need to find a common denominator. This is a number that is a multiple of both denominators. The common denominator allows us to express both fractions in terms of the same-sized parts, making addition possible.
Let's find a common denominator for 1/2 and 2/3. Multiples of 2 are 2, 4, 6, 8, 10... Multiples of 3 are 3, 6, 9, 12... The smallest number that appears in both lists is 6. Therefore, 6 is the least common denominator (LCD).
Converting Fractions to Equivalent Fractions with the Common Denominator
Now that we have the LCD (6), we need to convert both fractions to equivalent fractions with a denominator of 6. To do this, we multiply both the numerator and the denominator of each fraction by the same number so that the denominator becomes 6. This maintains the value of the fraction:
- For 1/2: To get a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
- For 2/3: To get a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
Adding the Fractions with the Common Denominator
Now that both fractions have the same denominator, we can add them by simply adding the numerators and keeping the common denominator:
3/6 + 4/6 = (3 + 4) / 6 = 7/6
The result is 7/6.
Simplifying the Fraction (if necessary)
The fraction 7/6 is an improper fraction because the numerator (7) is larger than the denominator (6). We can simplify this by converting it to a mixed number. A mixed number consists of a whole number and a proper fraction.
To convert 7/6 to a mixed number, we divide the numerator (7) by the denominator (6):
7 ÷ 6 = 1 with a remainder of 1
This means 7/6 is equal to 1 and 1/6.
Therefore, the answer to 1/2 + 2/3 is 7/6 or 1 1/6.
Step-by-Step Summary: Adding 1/2 and 2/3
Here's a concise summary of the steps involved:
- Find the least common denominator (LCD): The LCD of 2 and 3 is 6.
- Convert fractions to equivalent fractions with the LCD:
- 1/2 becomes 3/6 (multiply numerator and denominator by 3)
- 2/3 becomes 4/6 (multiply numerator and denominator by 2)
- Add the numerators, keeping the common denominator: 3/6 + 4/6 = 7/6
- Simplify the fraction (if necessary): 7/6 simplifies to the mixed number 1 1/6.
The Science Behind Fraction Addition
The process of finding a common denominator is fundamentally about ensuring we're adding like quantities. We're working with parts of a whole, and those parts must be of equal size for accurate addition. The common denominator establishes this equality, allowing for a meaningful summation. This concept extends to more complex fraction operations and forms the basis of algebra and calculus.
Frequently Asked Questions (FAQ)
-
What if the denominators have common factors? Finding the least common denominator (LCD) simplifies the process. If you use a common denominator that's not the least, you'll still get the correct answer but will need to simplify the final fraction further.
-
Can I add fractions with different denominators directly? No. You must first find a common denominator and convert the fractions to equivalent fractions with that denominator before adding them.
-
What if I have more than two fractions to add? The process remains the same; find the LCD for all the denominators and convert all the fractions before adding.
-
Are there any shortcuts for finding the LCD? For smaller denominators, it's often easy to find the LCD by inspection. For larger numbers, prime factorization can be helpful in identifying the LCD efficiently.
-
Why is it important to learn fraction addition? Understanding fraction addition is crucial for various applications in everyday life, including cooking, measuring, budgeting, and many fields of science and engineering. It's a foundational concept in mathematics.
Conclusion: Mastering Fraction Addition
Adding fractions might seem daunting at first, but by breaking down the process into manageable steps – identifying the common denominator, converting to equivalent fractions, adding the numerators, and simplifying the result – it becomes a straightforward and logical operation. Understanding the underlying principles of fraction addition is essential for building a solid foundation in mathematics and for tackling more advanced mathematical concepts in the future. Remember, practice makes perfect! The more you work with fractions, the more comfortable and proficient you'll become. So, grab a pencil and paper, and start practicing! You've got this!
Latest Posts
Latest Posts
-
Animal Farm Chapter 4 Summary
Sep 20, 2025
-
Difference Of Lake And River
Sep 20, 2025
-
Map Of The Northern Hemisphere
Sep 20, 2025
-
Well Known Places In Brazil
Sep 20, 2025
-
Discount Allowed Debit Or Credit
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 + 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.