Square Root Of 1 9
marihuanalabs
Sep 20, 2025 · 6 min read
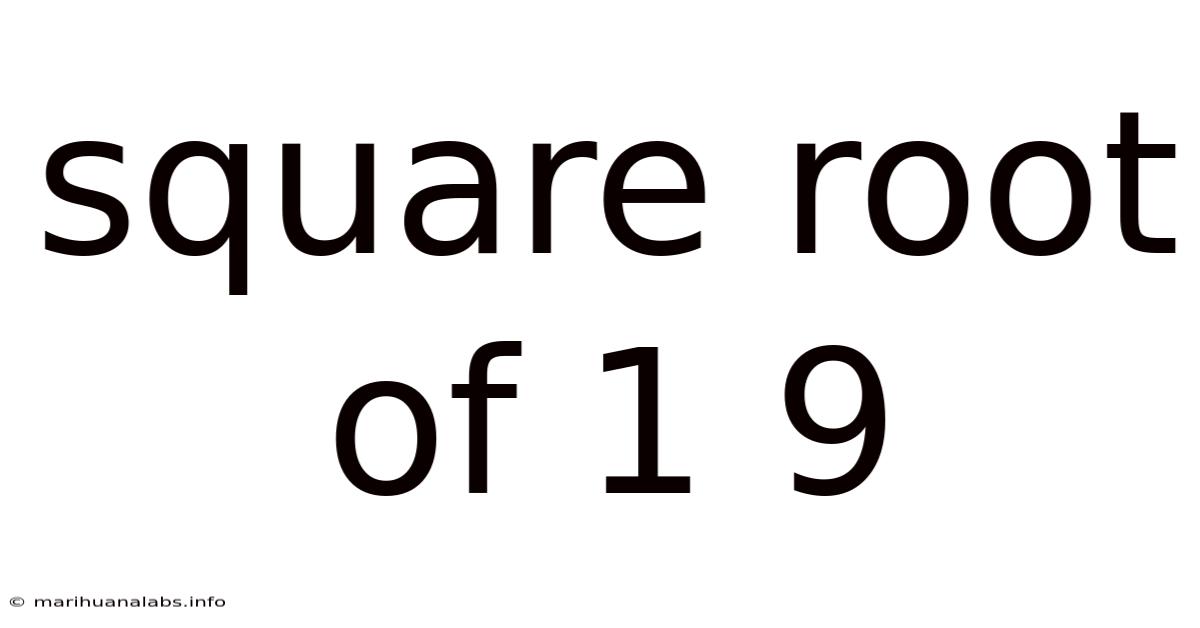
Table of Contents
Understanding the Square Root of 19: A Deep Dive into Irrational Numbers
The square root of 19, denoted as √19, is a fascinating number that exemplifies the beauty and complexity of mathematics. This article will explore √19 in detail, moving beyond a simple calculator answer to understand its properties, how it's calculated, and its significance within the broader mathematical landscape. We'll delve into its irrational nature, methods of approximation, and its applications in various fields. Understanding √19 provides valuable insight into the world of irrational numbers and their role in advanced mathematics and real-world applications.
What is the Square Root?
Before diving into the specifics of √19, let's revisit the fundamental concept of a square root. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. This is also known as finding the principal square root; however, it's important to note that both 3 and -3 when squared equal 9. But the principal square root is always the non-negative value.
This concept applies to all non-negative real numbers. However, things get a bit more interesting when we consider numbers that don't have perfect square roots—numbers like 19.
Why √19 is Irrational
Unlike the square root of 9 or 16, which are whole numbers (3 and 4 respectively), the square root of 19 is an irrational number. An irrational number is a number that cannot be expressed as a simple fraction (a ratio of two integers). Its decimal representation goes on forever without repeating. This means we can only approximate √19, not express it exactly as a fraction or a terminating decimal.
The proof that √19 is irrational is based on the method of contradiction. We assume √19 is rational, meaning it can be expressed as a fraction a/b where 'a' and 'b' are integers and b ≠ 0, and a and b are coprime (meaning they have no common factors other than 1). If √19 = a/b, then squaring both sides gives us 19 = a²/b². This implies that 19b² = a². Since 19 divides the left side, it must also divide the right side (a²). Because 19 is a prime number, it must also divide 'a'. Therefore, we can write a = 19k for some integer k.
Substituting this back into the equation, we get 19b² = (19k)² = 361k². Dividing both sides by 19, we have b² = 19k². This shows that 19 also divides b². And since 19 is prime, it must also divide 'b'.
But this contradicts our initial assumption that 'a' and 'b' are coprime, as they both share a common factor of 19. This contradiction proves that our initial assumption—that √19 is rational—must be false. Therefore, √19 is irrational.
Approximating √19
Since we can't express √19 exactly, we rely on approximation methods. Several approaches exist:
-
Babylonian Method (or Heron's Method): This iterative method refines an initial guess to get closer to the actual value. We start with an initial guess (let's say 4, since 4² = 16 is close to 19). Then we repeatedly apply the formula: x_(n+1) = 0.5 * (x_n + 19/x_n), where x_n is the current guess and x_(n+1) is the next guess. Each iteration brings us closer to the true value.
-
Calculator: Modern calculators provide a highly accurate approximation of √19. A calculator will typically show a value around 4.35889894...
-
Taylor Series Expansion: For those comfortable with calculus, the Taylor series expansion can approximate the square root function around a known point. This method involves an infinite series, but truncating the series after a few terms provides a reasonable approximation.
Numerical Calculation and Error Analysis
Let's illustrate the Babylonian method with a couple of iterations:
Iteration 1:
- x_0 = 4 (our initial guess)
- x_1 = 0.5 * (4 + 19/4) = 0.5 * (4 + 4.75) = 4.375
Iteration 2:
- x_1 = 4.375
- x_2 = 0.5 * (4.375 + 19/4.375) ≈ 4.3589
As you can see, even after just two iterations, we've obtained a reasonably accurate approximation. The more iterations we perform, the closer we get to the true value of √19.
It is important to note that any approximation will inherently have an error. Error analysis is crucial in many applications, and understanding the magnitude of the error in our approximation is essential for ensuring accuracy in calculations. The error can be calculated by subtracting the approximated value from the true value (as far as it's practically possible to find the true value), however, since √19 is irrational, the calculation will have to stop somewhere.
√19 in Geometry and Other Applications
The square root of 19, while seemingly abstract, appears in various practical applications:
-
Geometry: Imagine a right-angled triangle with legs of length 'a' and 'b', and hypotenuse 'c'. If a² + b² = 19, then the length of the hypotenuse is √19. This has implications in various fields requiring geometrical calculations, such as surveying, engineering, and computer graphics.
-
Physics: Many physical phenomena involve square roots in their formulas. For example, in calculations involving velocity, energy, or forces, we might encounter expressions that include √19.
-
Statistics and Probability: In statistics, √19 can appear in calculations involving standard deviation or statistical significance.
-
Computer Science: Approximating irrational numbers like √19 is a crucial task in computer graphics, simulations, and other computational fields that deal with continuous data.
Frequently Asked Questions (FAQ)
-
Q: Is √19 a rational or irrational number?
-
A: √19 is an irrational number. It cannot be expressed as a fraction of two integers.
-
Q: What is the approximate value of √19?
-
A: The approximate value of √19 is approximately 4.3589.
-
Q: How can I calculate √19 without a calculator?
-
A: You can use methods like the Babylonian method (Heron's method) to approximate √19 through iterative calculations.
-
Q: What are some real-world applications of √19?
-
A: √19 finds applications in geometry, physics, statistics, and computer science, among other fields, often arising in calculations involving Pythagoras' theorem or other formulas containing square roots.
-
Q: Why is it important to understand irrational numbers like √19?
-
A: Understanding irrational numbers expands our mathematical knowledge beyond simple fractions and decimals. It's crucial for comprehending advanced mathematical concepts and for solving problems in various scientific and engineering disciplines. Approximating irrational numbers accurately is also a critical skill in many computational fields.
Conclusion
The square root of 19, while not a simple whole number, is a significant mathematical concept that demonstrates the properties of irrational numbers. Its calculation, approximation, and applications highlight the interconnectedness of various mathematical fields and their relevance in the real world. Whether you are a student of mathematics, an engineer, or simply curious about numbers, understanding √19 provides a richer appreciation for the complexity and beauty of mathematics. The ability to approximate irrational numbers using methods like the Babylonian method also serves as a fundamental skill in numerous computational tasks. Ultimately, exploring the seemingly simple √19 unlocks a deeper understanding of the broader mathematical landscape.
Latest Posts
Latest Posts
-
J Adore Meaning In English
Sep 20, 2025
-
Passed Of Time Crossword Clue
Sep 20, 2025
-
What Is 75grams In Ounces
Sep 20, 2025
-
Particular Solutions For Differential Equations
Sep 20, 2025
-
Normal Sodium Levels In Urine
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 1 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.