Prime Factor Tree For 220
marihuanalabs
Sep 15, 2025 · 6 min read
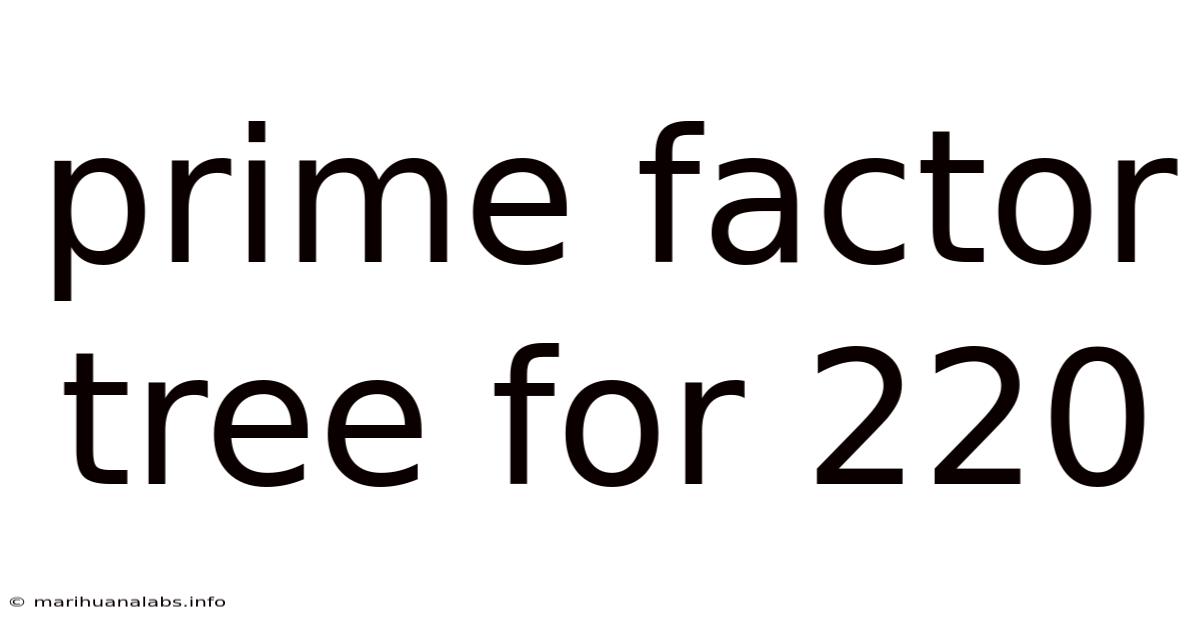
Table of Contents
Unveiling the Prime Factors of 220: A Deep Dive into Prime Factorization using Factor Trees
Finding the prime factors of a number might seem like a dry mathematical exercise, but it's a fundamental concept in number theory with applications in cryptography, computer science, and even music theory! This article will guide you through the process of prime factorization, specifically focusing on the number 220, using a prime factor tree. We'll not only show you how to do it but also why it's important and explore some related mathematical concepts. Understanding prime factorization is a key step towards mastering more advanced mathematical concepts.
What is Prime Factorization?
Prime factorization is the process of breaking down a composite number (a number greater than 1 that is not prime) into its prime factors. A prime number is a natural number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Every composite number can be expressed uniquely as a product of prime numbers. This uniqueness is guaranteed by the Fundamental Theorem of Arithmetic.
The Prime Factor Tree Method: A Visual Approach
The prime factor tree is a visual method to represent the prime factorization process. It's particularly helpful for understanding the steps involved, especially for larger numbers. Let's build the prime factor tree for 220:
-
Start with the number: Write 220 at the top of your tree.
-
Find the smallest prime factor: The smallest prime number is 2. Since 220 is an even number, it's divisible by 2.
-
Branch out: Draw two branches extending downwards from 220. On the left branch, write 2 (the prime factor we found). On the right branch, write the result of dividing 220 by 2, which is 110.
-
Repeat the process: Now we focus on 110. Again, 110 is divisible by 2. Draw two branches from 110. On the left, write 2. On the right, write 55 (110 divided by 2).
-
Continue until you reach prime numbers: Now we have 55. 55 is not divisible by 2, but it is divisible by 5. Draw two branches from 55. On the left, write 5. On the right, write 11 (55 divided by 5).
-
End of the line: Both 5 and 11 are prime numbers. This means we've reached the end of our prime factor tree.
Here's a visual representation of the prime factor tree for 220:
220
/ \
2 110
/ \
2 55
/ \
5 11
- Write out the prime factorization: The prime factors we found are 2, 2, 5, and 11. Therefore, the prime factorization of 220 is 2 x 2 x 5 x 11, or 2² x 5 x 11.
Understanding the Uniqueness of Prime Factorization
The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This means that no matter how you approach the prime factorization of 220 using a factor tree (different starting prime factors are possible), you will always end up with the same set of prime factors: 2, 2, 5, and 11. This uniqueness is crucial in various mathematical applications.
Beyond the Factor Tree: Alternative Methods
While the prime factor tree is a visually intuitive method, other methods exist for prime factorization. One common alternative is the division method:
-
Start with the number: Begin with the number 220.
-
Divide by the smallest prime factor: Divide 220 by 2, resulting in 110.
-
Repeat: Divide 110 by 2, resulting in 55.
-
Continue with other prime factors: 55 is not divisible by 2, but it's divisible by 5. Divide 55 by 5, resulting in 11.
-
End: 11 is a prime number. The process is complete.
The prime factors obtained are the same: 2, 2, 5, and 11. This demonstrates the uniqueness guaranteed by the Fundamental Theorem of Arithmetic.
Applications of Prime Factorization
Prime factorization, while seemingly simple, has far-reaching applications:
-
Cryptography: Many modern encryption methods rely heavily on the difficulty of factoring very large numbers into their prime factors. RSA encryption, a widely used algorithm for secure communication, is based on this principle. The larger the numbers, the harder it is to factor them, ensuring the security of the encrypted information.
-
Computer Science: Prime numbers play a critical role in various algorithms and data structures in computer science. For example, they are used in hash table design and in generating unique identifiers.
-
Number Theory: Prime factorization is a fundamental concept in number theory, forming the basis for exploring various properties of numbers, such as divisibility, greatest common divisors (GCD), and least common multiples (LCM).
-
Music Theory: Interestingly, prime numbers have connections to music theory. Some musical scales and harmonies can be analyzed using prime numbers, revealing underlying mathematical structures within musical compositions.
Frequently Asked Questions (FAQ)
Q: Is there a limit to the size of a number that can be prime factorized?
A: Theoretically, no. However, practically, factoring extremely large numbers becomes computationally very intensive. This is precisely why it's used in cryptography—the difficulty of factoring large numbers ensures security.
Q: What if I choose a different prime factor to start with in the factor tree?
A: You'll still get the same set of prime factors, just in a different order. The Fundamental Theorem of Arithmetic guarantees this uniqueness. For instance, you could start by dividing 220 by 5 first, then 11, and finally by 2 twice. The result will be the same: 2² x 5 x 11.
Q: Are there any shortcuts or tricks for prime factorization?
A: For smaller numbers, trial division is often sufficient. For larger numbers, more sophisticated algorithms are needed, but these are beyond the scope of this introductory article.
Q: How can I improve my skills in prime factorization?
A: Practice is key! Start with smaller numbers and gradually work your way up to larger ones. Use different methods like factor trees and division to build your understanding and comfort level.
Conclusion
Prime factorization of 220, as demonstrated through the prime factor tree and division methods, reveals its fundamental composition: 2² x 5 x 11. This seemingly simple process is a cornerstone of number theory and holds significant importance in various fields, highlighting the profound connections between seemingly abstract mathematical concepts and practical applications in the real world. Mastering prime factorization enhances your understanding of numbers and opens doors to more complex mathematical concepts and their real-world applications. Remember that consistent practice and a curious mindset are key to unlocking the fascinating world of number theory!
Latest Posts
Latest Posts
-
What Is 25mm In Inches
Sep 15, 2025
-
Meaning Of Hamza In Islam
Sep 15, 2025
-
Father Of Odysseus Crossword Clue
Sep 15, 2025
-
What Is 20 Of 18
Sep 15, 2025
-
Internal Factors Of A Business
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 220 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.