Prime Factor Tree For 198
marihuanalabs
Sep 11, 2025 · 6 min read
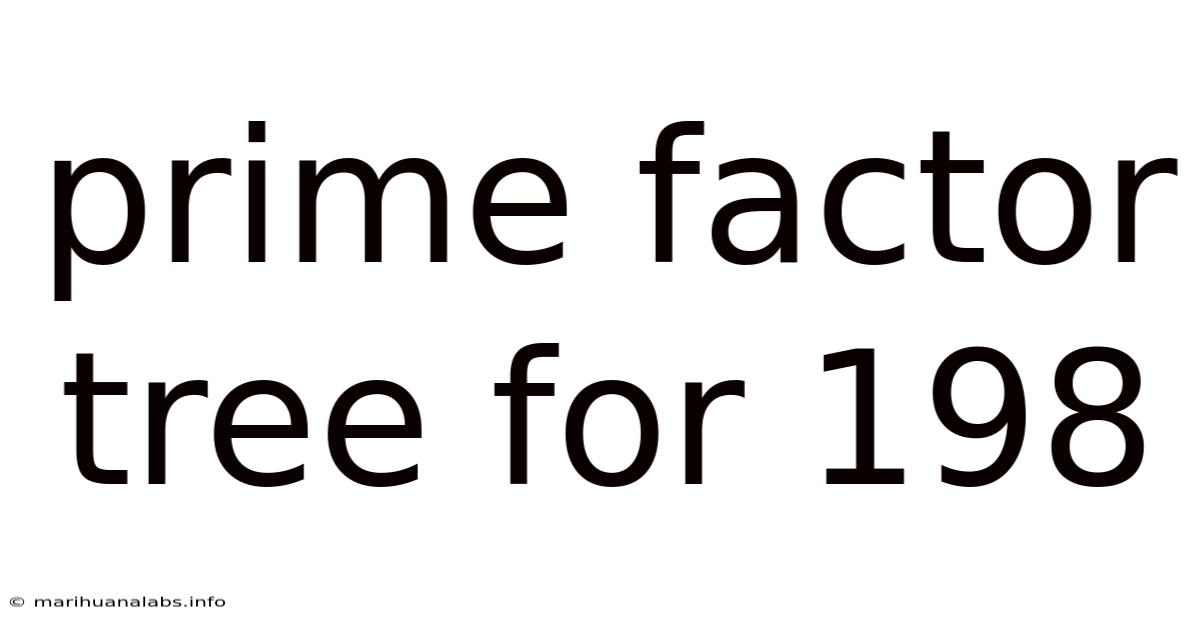
Table of Contents
Unveiling the Prime Factorization of 198: A Comprehensive Guide to Prime Factor Trees
Finding the prime factorization of a number might seem like a dry mathematical exercise, but it's a fundamental concept with far-reaching applications in algebra, cryptography, and even computer science. This article will delve into the process of determining the prime factorization of 198 using the prime factor tree method, explaining the underlying principles and offering a step-by-step guide suitable for learners of all levels. We'll also explore the significance of prime factorization and answer frequently asked questions. Understanding prime factorization is key to mastering various mathematical concepts, and this detailed explanation will help solidify your understanding.
Understanding Prime Numbers and Factorization
Before we embark on our journey to find the prime factorization of 198, let's revisit the basic definitions. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. A number that is not prime is called a composite number.
Factorization, in its simplest form, is the process of breaking down a composite number into its smaller constituent parts, which are its factors. Prime factorization, specifically, involves expressing a composite number as a product of its prime factors. This representation is unique for every number, meaning there's only one way to express a number as a product of prime factors (ignoring the order of the factors).
Constructing the Prime Factor Tree for 198
The prime factor tree is a visual method to find the prime factorization of a number. It's a systematic approach that involves repeatedly dividing the number by its smallest prime factor until you are left with only prime numbers. Let's construct the prime factor tree for 198:
-
Start with the number 198: We begin by writing 198 at the top of our tree.
-
Find the smallest prime factor: The smallest prime factor of 198 is 2 (because 198 is an even number). We divide 198 by 2, resulting in 99. We represent this on the tree by drawing two branches from 198, one leading to 2 and the other to 99.
-
Continue the process: Now we focus on 99. The smallest prime factor of 99 is 3. Dividing 99 by 3 gives us 33. We add branches from 99, one leading to 3 and the other to 33.
-
Repeat until all factors are prime: We continue with 33. Its smallest prime factor is also 3. Dividing 33 by 3 gives us 11. We add branches from 33, one leading to 3 and the other to 11.
-
Identify the prime factors: We've reached the end of the process because 11 is a prime number. Looking at the end points of our branches, we have 2, 3, 3, and 11. These are the prime factors of 198.
Therefore, the prime factorization of 198 is 2 x 3 x 3 x 11, which can also be written as 2 x 3² x 11.
Here's a visual representation of the prime factor tree for 198:
198
/ \
2 99
/ \
3 33
/ \
3 11
Alternative Methods for Finding Prime Factorization
While the prime factor tree is a visually intuitive method, there are other ways to find the prime factorization of a number. One such method is repeated division. This involves repeatedly dividing the number by its smallest prime factor until you reach 1. The prime factors used in the division process constitute the prime factorization.
For 198:
- 198 ÷ 2 = 99
- 99 ÷ 3 = 33
- 33 ÷ 3 = 11
- 11 ÷ 11 = 1
The prime factors are 2, 3, 3, and 11. This confirms the result we obtained using the prime factor tree method.
The Significance of Prime Factorization
Prime factorization might seem like a simple mathematical operation, but it has significant implications across several fields:
-
Cryptography: Many modern encryption methods, such as RSA encryption, rely heavily on the difficulty of factoring large numbers into their prime components. The security of these systems depends on the computational complexity of this task.
-
Number Theory: Prime factorization is fundamental to many theorems and concepts in number theory, a branch of mathematics that studies the properties of integers.
-
Algebra: Prime factorization plays a crucial role in simplifying algebraic expressions and solving equations.
-
Computer Science: Algorithms for prime factorization are used in various computer science applications, including cryptography and data security.
Frequently Asked Questions (FAQ)
Q1: What if I choose a different prime factor to start with?
A1: While you can start with a different prime factor, you will ultimately arrive at the same prime factorization. The order of the prime factors might differ, but the set of prime factors will remain the same. This is due to the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (disregarding the order).
Q2: How do I know if a number is prime?
A2: There are various methods to determine if a number is prime. For smaller numbers, you can check if it's divisible only by 1 and itself. For larger numbers, more sophisticated algorithms like the Sieve of Eratosthenes are employed.
Q3: Are there any limitations to the prime factor tree method?
A3: While the prime factor tree method is effective for smaller numbers, it can become cumbersome for very large numbers. More efficient algorithms are necessary for factoring extremely large composite numbers.
Q4: What are some real-world applications of prime factorization besides cryptography?
A4: Prime factorization finds its applications in simplifying fractions, solving Diophantine equations (equations where solutions are integers), and in various coding and algorithm optimization problems in computer science. Understanding prime numbers and their distribution also has implications in the field of probability and statistics.
Conclusion
Understanding prime factorization is a cornerstone of mathematical literacy. The prime factor tree method provides a clear and visual way to break down composite numbers into their prime components. This process, while seemingly simple, underpins many advanced mathematical concepts and has far-reaching implications in diverse fields like cryptography and computer science. By mastering this fundamental skill, you’re not just learning about numbers; you’re gaining access to a deeper understanding of how mathematics structures our world. Remember to practice, explore different methods, and don’t hesitate to delve deeper into the fascinating world of prime numbers! The journey of mathematical discovery is a rewarding one, and the ability to factorize numbers efficiently is a valuable tool along the way.
Latest Posts
Latest Posts
-
Patriarch In Genesis Crossword Clue
Sep 11, 2025
-
Advantage Of A Electron Microscope
Sep 11, 2025
-
Series And Parallel Circuits Capacitors
Sep 11, 2025
-
How To Measure Photosynthetic Rate
Sep 11, 2025
-
French Verbs Ending In Er
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 198 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.