Prime Factor Decomposition Of 396
marihuanalabs
Sep 10, 2025 · 5 min read
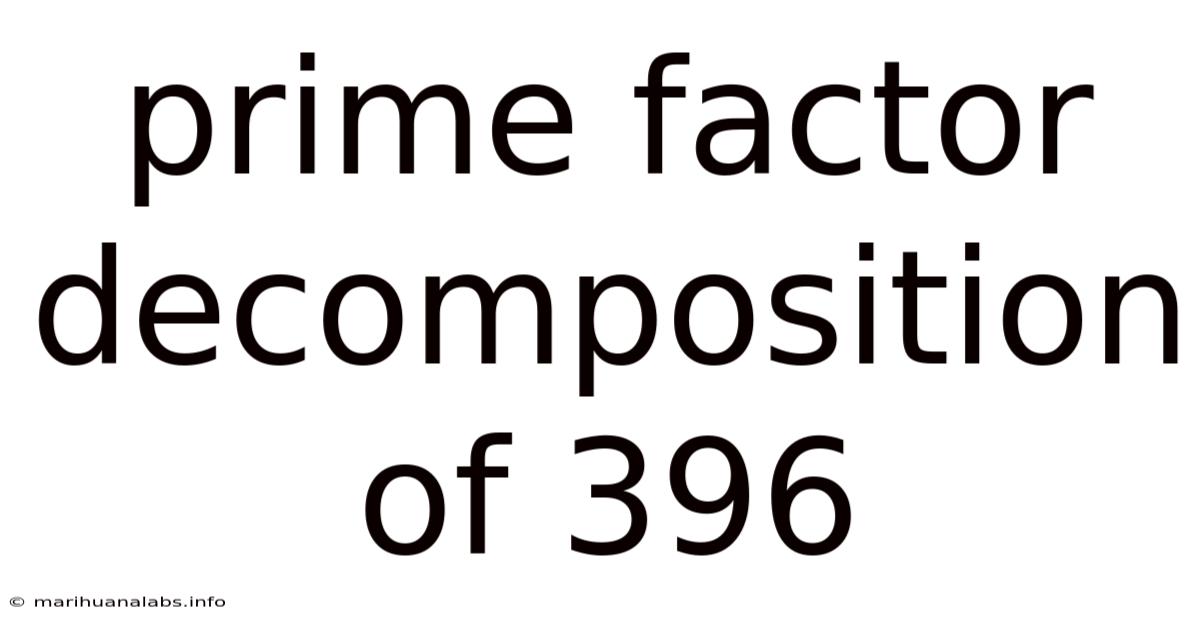
Table of Contents
Unveiling the Prime Factors of 396: A Deep Dive into Prime Factorization
Prime factorization, the process of breaking down a number into its prime constituents, is a fundamental concept in number theory. Understanding prime factorization is crucial for various mathematical operations, including simplifying fractions, finding the greatest common divisor (GCD), and the least common multiple (LCM). This article will explore the prime factorization of 396, providing a step-by-step guide, a deeper look into the underlying mathematical principles, frequently asked questions, and concluding remarks to solidify your understanding. This comprehensive exploration will equip you with the skills to tackle similar factorization problems with confidence.
Introduction to Prime Factorization
Before we delve into the specific factorization of 396, let's establish a foundational understanding of prime numbers and prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. Numbers that are not prime are called composite numbers.
Prime factorization is the process of expressing a composite number as a product of its prime factors. Every composite number can be uniquely represented as a product of prime numbers, a principle known as the Fundamental Theorem of Arithmetic. This uniqueness is a cornerstone of number theory, enabling numerous mathematical applications.
Step-by-Step Prime Factorization of 396
Let's now systematically find the prime factorization of 396. We'll use a method commonly referred to as the "factor tree."
-
Start with the smallest prime number: The smallest prime number is 2. Since 396 is an even number (divisible by 2), we begin by dividing 396 by 2:
396 ÷ 2 = 198
-
Continue dividing by prime numbers: 198 is also an even number, so we divide again by 2:
198 ÷ 2 = 99
-
Move to the next prime number: 99 is no longer divisible by 2. The next prime number is 3. 99 is divisible by 3:
99 ÷ 3 = 33
-
Repeat the process: 33 is also divisible by 3:
33 ÷ 3 = 11
-
End with a prime number: 11 is a prime number. We have reached the end of our factorization.
Therefore, the prime factorization of 396 is 2 x 2 x 3 x 3 x 11, which can be written more concisely as 2² x 3² x 11.
Visualizing the Factor Tree for 396
A factor tree provides a visual representation of the process:
396
/ \
2 198
/ \
2 99
/ \
3 33
/ \
3 11
This tree clearly shows the successive divisions by prime numbers until we arrive at only prime factors at the bottom branches.
Mathematical Explanation and Properties
The prime factorization of 396 (2² x 3² x 11) reveals several important properties:
- Even Number: The presence of the factor 2 indicates that 396 is an even number.
- Divisibility Rules: The factors 2 and 3 demonstrate that 396 is divisible by both 2 and 3. This aligns with divisibility rules: a number is divisible by 2 if its last digit is even, and a number is divisible by 3 if the sum of its digits is divisible by 3 (3 + 9 + 6 = 18, which is divisible by 3).
- Number of Divisors: The number of divisors of 396 can be calculated using the exponents in its prime factorization. Adding 1 to each exponent and multiplying the results gives the total number of divisors: (2+1) x (2+1) x (1+1) = 18. This means 396 has 18 divisors (including 1 and 396 itself).
- Perfect Square: 396 is not a perfect square because not all exponents in its prime factorization are even. A perfect square's prime factorization has all even exponents.
- Applications in Number Theory: The prime factorization is essential in various number theory problems, such as finding the GCD and LCM of numbers. For example, if we want to find the GCD of 396 and another number, we can compare their prime factorizations to identify common factors.
Alternative Methods of Prime Factorization
While the factor tree method is intuitive and visually appealing, there are other approaches to prime factorization:
-
Division Method: This method involves systematically dividing the number by prime numbers, starting with the smallest, until you reach 1. Keep track of the prime divisors used.
-
Using a Prime Factorization Calculator: Many online calculators can quickly find the prime factorization of a number. These tools can be helpful for larger numbers where manual factorization becomes tedious.
Frequently Asked Questions (FAQ)
-
Q: What is the significance of prime factorization?
A: Prime factorization is fundamental in number theory and has applications in cryptography, computer science, and other fields. It's crucial for simplifying fractions, finding GCD and LCM, and understanding the divisibility properties of numbers.
-
Q: Is there only one prime factorization for a given number?
A: Yes, according to the Fundamental Theorem of Arithmetic, every composite number has a unique prime factorization (disregarding the order of the factors).
-
Q: How do I find the prime factorization of a very large number?
A: For very large numbers, specialized algorithms and computer programs are often used. These algorithms are far more efficient than manual methods.
-
Q: What are some real-world applications of prime factorization?
A: Prime factorization is crucial in cryptography, especially in public-key cryptosystems like RSA. The difficulty of factoring large numbers into their prime factors is the basis of the security of these systems.
Conclusion
Prime factorization, a seemingly simple concept, reveals a rich mathematical structure. The systematic breakdown of 396 into its prime factors (2² x 3² x 11) showcases the beauty and power of this fundamental concept. This process not only provides the prime factors but also allows us to understand divisibility, calculate the number of divisors, and explore more advanced concepts in number theory. Understanding prime factorization lays a strong foundation for further exploration in mathematics and its diverse applications. Mastering this skill will undoubtedly enhance your mathematical prowess and problem-solving capabilities. The ability to efficiently find prime factors enables you to tackle more complex numerical problems with ease and confidence. Through this in-depth analysis of 396, we have not only solved a specific problem but have also expanded our understanding of the broader mathematical principles at play. Remember, practice is key to mastering prime factorization!
Latest Posts
Latest Posts
-
House Of Leaves Book Summary
Sep 10, 2025
-
Sodium Hydroxide And Ammonium Chloride
Sep 10, 2025
-
One Tenth As A Decimal
Sep 10, 2025
-
Time And Motion Study Sample
Sep 10, 2025
-
Insects That Look Like Ticks
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Decomposition Of 396 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.