Prime Factor Decomposition Of 252
marihuanalabs
Sep 06, 2025 · 5 min read
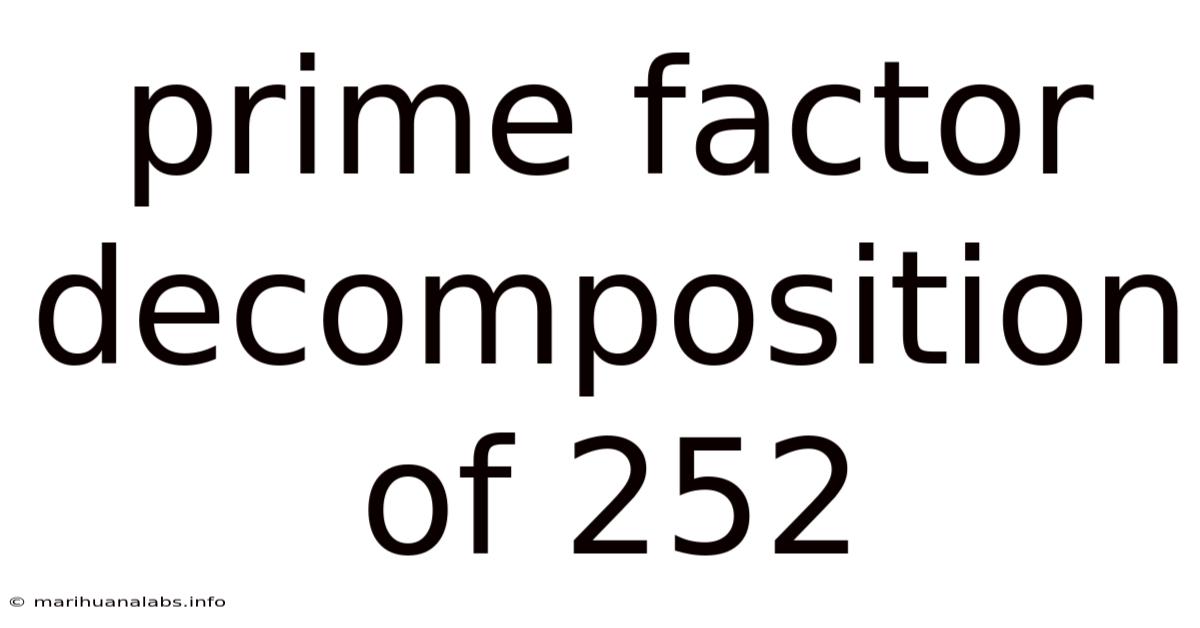
Table of Contents
Unveiling the Prime Factors of 252: A Deep Dive into Prime Factorization
Prime factorization, the process of breaking down a number into its prime number components, is a fundamental concept in mathematics. Understanding prime factorization is crucial for various mathematical operations, from simplifying fractions to solving complex equations. This article will delve into the prime factor decomposition of 252, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing frequently asked questions. We'll also touch upon the broader significance of prime factorization in number theory. By the end, you'll not only know the prime factors of 252 but also grasp the core concepts behind this essential mathematical technique.
Understanding Prime Numbers and Prime Factorization
Before we embark on the prime factorization of 252, let's establish a clear understanding of the key terms. A prime number is a natural number greater than 1 that has only two distinct positive divisors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. A number that is not prime is called a composite number.
Prime factorization, also known as prime decomposition, is the process of expressing a composite number as a product of its prime factors. This representation is unique for every composite number; meaning, there's only one way to write a number as a product of its prime factors (excluding the order of the factors). This uniqueness is guaranteed by the Fundamental Theorem of Arithmetic.
Step-by-Step Prime Factorization of 252
Now, let's tackle the prime factorization of 252. We'll use the method of repeated division by prime numbers.
-
Start with the smallest prime number, 2: 252 is an even number, so it's divisible by 2. 252 ÷ 2 = 126.
-
Continue dividing by 2: 126 is also even, so we can divide by 2 again. 126 ÷ 2 = 63.
-
Move to the next prime number, 3: 63 is divisible by 3 (because the sum of its digits, 6 + 3 = 9, is divisible by 3). 63 ÷ 3 = 21.
-
Divide by 3 again: 21 is also divisible by 3. 21 ÷ 3 = 7.
-
The final result is a prime number, 7: 7 is a prime number, so we've reached the end of our factorization.
Therefore, the prime factorization of 252 is 2 x 2 x 3 x 3 x 7, which can be written more concisely as 2² x 3² x 7.
Visualizing the Prime Factorization: Factor Tree
A helpful visual aid for prime factorization is a factor tree. Here's how the factor tree for 252 would look:
252
/ \
2 126
/ \
2 63
/ \
3 21
/ \
3 7
The factor tree clearly shows the steps involved in breaking down 252 into its prime factors. Each branch ends with a prime number.
Mathematical Significance of Prime Factorization
The seemingly simple process of prime factorization has profound implications within mathematics and beyond. Here are some key areas where it plays a vital role:
-
Simplifying Fractions: Prime factorization is crucial for simplifying fractions to their lowest terms. By finding the common factors in the numerator and denominator, we can cancel them out, resulting in a simpler fraction.
-
Finding the Greatest Common Divisor (GCD) and Least Common Multiple (LCM): The GCD and LCM of two or more numbers are easily determined using their prime factorizations. The GCD is the product of the common prime factors raised to the lowest power, while the LCM is the product of all prime factors raised to the highest power.
-
Cryptography: Prime numbers and their properties are fundamental to modern cryptography, especially in public-key cryptography systems like RSA. The difficulty of factoring large numbers into their prime components is the basis for the security of these systems.
-
Number Theory: Prime factorization is a cornerstone of number theory, a branch of mathematics that studies the properties of integers. Many theorems and conjectures in number theory rely on the properties of prime numbers and their factorization.
-
Algebra: Prime factorization is used in algebraic manipulations, particularly when dealing with polynomial expressions. Factoring polynomials is analogous to prime factorizing integers.
Alternative Methods for Prime Factorization
While repeated division is a straightforward method, other approaches can be used for prime factorization, particularly for larger numbers. These include:
-
Trial Division: Systematically testing divisibility by prime numbers, starting with the smallest. This method can be time-consuming for very large numbers.
-
Sieve of Eratosthenes: This is an efficient algorithm for finding all prime numbers up to a specified limit. While not directly a factorization method, it provides a list of potential prime divisors to use in trial division.
-
Specialized Algorithms: For extremely large numbers, sophisticated algorithms like the General Number Field Sieve (GNFS) are employed. These algorithms are computationally intensive but necessary for factoring numbers used in cryptography.
Frequently Asked Questions (FAQ)
Q1: Why is the prime factorization of a number unique?
A1: The uniqueness of prime factorization is guaranteed by the Fundamental Theorem of Arithmetic. This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors.
Q2: What is the significance of the exponents in the prime factorization (e.g., 2² x 3² x 7)?
A2: The exponents indicate the number of times each prime factor appears in the factorization. In the case of 252 (2² x 3² x 7), the prime factor 2 appears twice, 3 appears twice, and 7 appears once.
Q3: How can I check if my prime factorization is correct?
A3: Multiply all the prime factors together. If the result equals the original number (252 in this case), your factorization is correct.
Q4: Is there a limit to the size of numbers that can be prime factorized?
A4: Theoretically, there is no limit. However, practically, the time and computational resources required to factorize extremely large numbers can become prohibitive. This is a key element in the security of many cryptographic systems.
Conclusion
The prime factorization of 252, 2² x 3² x 7, is not merely a simple mathematical exercise. It represents a foundational concept in number theory with widespread applications across various mathematical fields and beyond. Understanding the process, the underlying principles, and the significance of prime factorization equips you with a powerful tool for solving numerous mathematical problems and appreciating the elegance and depth of number theory. From simplifying fractions to understanding the security of online transactions, the seemingly simple act of breaking down a number into its prime components holds significant weight in the world of mathematics and technology.
Latest Posts
Latest Posts
-
Memoirs Of A Geisha Cast
Sep 06, 2025
-
Stash Or Conceal Crossword Clue
Sep 06, 2025
-
Summary God Of Small Things
Sep 06, 2025
-
South America Map And Mexico
Sep 06, 2025
-
Quotes About Gender In Macbeth
Sep 06, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Decomposition Of 252 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.