Lcm Of 30 And 45
marihuanalabs
Sep 23, 2025 · 6 min read
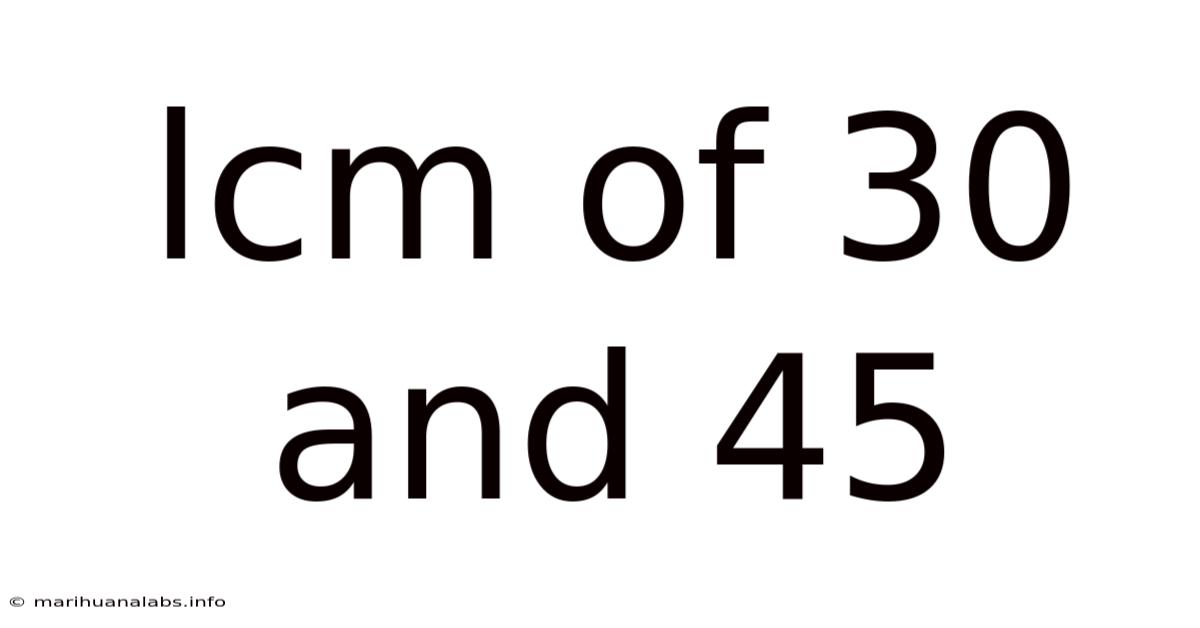
Table of Contents
Finding the LCM of 30 and 45: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and various methods for calculating it offers valuable insights into number theory and its practical applications. This article will explore the LCM of 30 and 45, not just by providing the answer, but by delving into multiple approaches, explaining the reasoning behind each, and highlighting the broader significance of LCMs in mathematics and real-world problems.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that both (or all) numbers divide into evenly. Understanding LCM is crucial in various mathematical contexts, from simplifying fractions to solving problems related to cycles and periodic events. This article will focus on finding the LCM of 30 and 45, using several methods to illustrate the concept and its versatility.
Method 1: Listing Multiples
This is the most straightforward approach, particularly for smaller numbers. We list the multiples of both 30 and 45 until we find the smallest common multiple.
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300...
- Multiples of 45: 45, 90, 135, 180, 225, 270, 315...
By comparing the two lists, we see that the smallest number appearing in both lists is 90. Therefore, the LCM of 30 and 45 is 90.
This method works well for small numbers, but it becomes inefficient for larger numbers where listing all multiples can be time-consuming and prone to errors.
Method 2: Prime Factorization
This method is more efficient and works for larger numbers. It relies on expressing each number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
-
Prime factorization of 30: 30 = 2 × 3 × 5
-
Prime factorization of 45: 45 = 3 × 3 × 5 = 3² × 5
-
Finding the LCM using prime factors: To find the LCM, we take the highest power of each prime factor present in either factorization and multiply them together.
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ (from 30).
- The highest power of 3 is 3² (from 45).
- The highest power of 5 is 5¹ (from both 30 and 45).
Therefore, LCM(30, 45) = 2¹ × 3² × 5¹ = 2 × 9 × 5 = 90
This method is more systematic and less prone to error than the listing method, especially for larger numbers. It's a fundamental concept in number theory and has wide applications.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (greatest common divisor) of two numbers are closely related. The GCD is the largest number that divides both numbers evenly. There's a formula that links the LCM and GCD:
LCM(a, b) × GCD(a, b) = a × b
-
Finding the GCD of 30 and 45: We can use the Euclidean algorithm to find the GCD.
- 45 = 30 × 1 + 15
- 30 = 15 × 2 + 0
The last non-zero remainder is the GCD, which is 15. Therefore, GCD(30, 45) = 15.
-
Using the formula: LCM(30, 45) = (30 × 45) / GCD(30, 45) = (30 × 45) / 15 = 1350 / 15 = 90
This method provides an alternative approach, particularly useful when dealing with larger numbers where prime factorization might be more challenging. The Euclidean algorithm is an efficient method for finding the GCD.
Method 4: Ladder Method (or Staircase Method)
This is a visual and intuitive method. We arrange the numbers and repeatedly divide by common factors until we reach 1. The product of the divisors and the remaining numbers is the LCM.
2 | 30 45
3 | 15 45
3 | 5 15
5 | 5 5
| 1 1
LCM(30, 45) = 2 × 3 × 3 × 5 = 90
This method combines elements of prime factorization and a clear visual representation, making it easier to understand the process.
The Significance of LCM in Real-World Applications:
The LCM has numerous practical applications beyond pure mathematics:
-
Scheduling: Imagine two buses leaving a station at different intervals. The LCM helps determine when both buses will depart at the same time again.
-
Calendars: Determining when certain events will coincide (e.g., the overlap of lunar and solar cycles).
-
Construction: In construction projects, materials often come in different lengths or quantities. The LCM helps determine the most efficient way to utilize these materials without waste.
-
Music: The LCM is used in music theory to determine the least common multiple of rhythmic values, helping in creating harmonized musical pieces.
-
Gears and Rotations: In mechanical systems involving gears, the LCM helps calculate when the gears will be in the same position again.
These are just a few examples; the applications of LCM are vast and varied across diverse fields.
Frequently Asked Questions (FAQs):
-
What if I want to find the LCM of more than two numbers? You can extend the prime factorization method or the ladder method to include more numbers. Find the prime factorization of each number, and then take the highest power of each prime factor present in any of the factorizations. Multiply these highest powers together to obtain the LCM.
-
Is there a formula for the LCM of three or more numbers? There isn't a single, concise formula like the one relating LCM and GCD for two numbers. However, the principle of using prime factorization to find the highest power of each prime factor remains the most efficient method.
-
Why is the LCM important in simplifying fractions? The LCM is crucial in finding a common denominator when adding or subtracting fractions with different denominators. Finding the LCM ensures that you are working with the smallest possible common denominator, making the calculations simpler.
Conclusion:
Finding the LCM of 30 and 45, as demonstrated through multiple methods, reveals more than just the answer (90). It showcases fundamental concepts in number theory, including prime factorization and the relationship between LCM and GCD. Understanding these methods empowers you to tackle more complex problems involving LCM and appreciate its significance in diverse real-world applications. The choice of method depends on the context and the size of the numbers involved, but the core principle remains consistent: finding the smallest positive integer that is a multiple of all the given integers. This understanding provides a strong foundation for further exploration of number theory and its practical uses.
Latest Posts
Latest Posts
-
Pablo Escobar Wife Still Alive
Sep 23, 2025
-
The Chronicles Of Narnia Video
Sep 23, 2025
-
Afro Cuban Music Crossword Clue
Sep 23, 2025
-
Formative Assessment Versus Summative Assessment
Sep 23, 2025
-
We Need New Names Book
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 30 And 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.