Lcm Of 3 And 5
marihuanalabs
Sep 21, 2025 · 6 min read
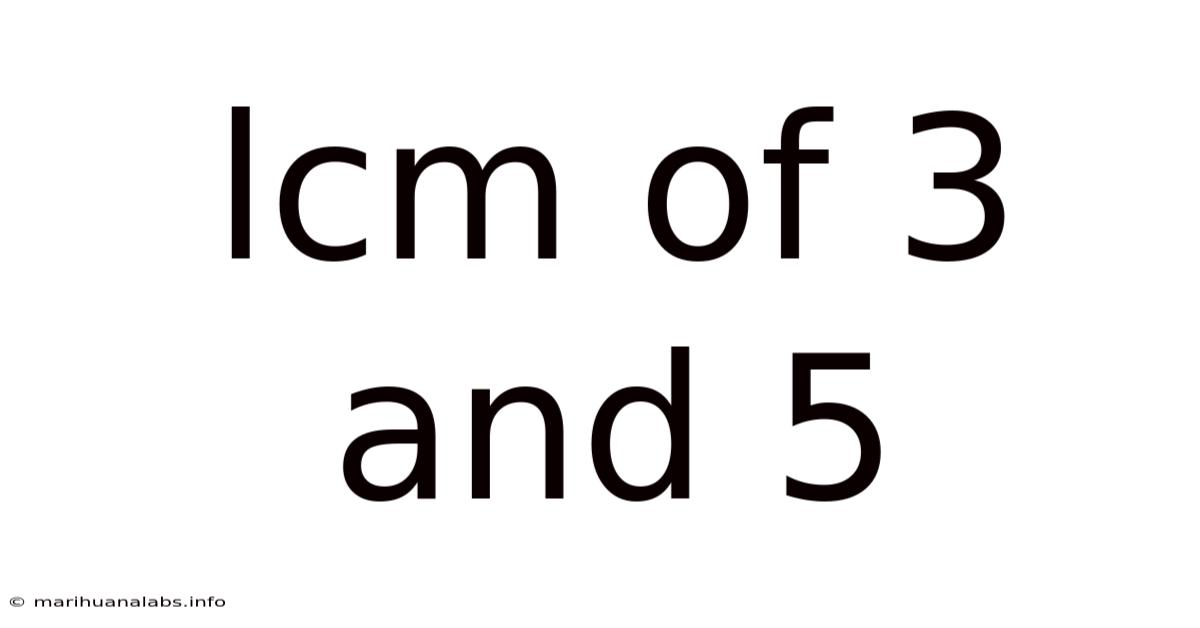
Table of Contents
Understanding the LCM of 3 and 5: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, but understanding the underlying concepts opens doors to more advanced mathematical concepts. This article delves deep into calculating and understanding the LCM of 3 and 5, exploring different methods and explaining the significance of LCMs in various mathematical applications. We'll go beyond a simple answer and explore the "why" behind the calculations, making this concept clear for learners of all levels.
What is a Least Common Multiple (LCM)?
Before we tackle the LCM of 3 and 5, let's define what a least common multiple actually is. The LCM of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers as factors. For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, 30, and so on. The smallest of these common multiples is 6. Therefore, the LCM of 2 and 3 is 6.
Calculating the LCM of 3 and 5: Three Approaches
Now, let's focus on finding the LCM of 3 and 5. We can use several methods to achieve this:
1. Listing Multiples:
This is the most straightforward method, especially for smaller numbers like 3 and 5. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
By comparing the lists, we can see that the smallest common multiple is 15. Therefore, the LCM of 3 and 5 is 15.
2. Prime Factorization Method:
This method is particularly useful for larger numbers. It involves breaking down each number into its prime factors. Prime factors are numbers divisible only by 1 and themselves (e.g., 2, 3, 5, 7, 11...).
- Prime factorization of 3: 3 (3 is a prime number itself)
- Prime factorization of 5: 5 (5 is a prime number itself)
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations of the numbers. In this case, we have 3 and 5 as prime factors. Therefore, the LCM is 3 x 5 = 15.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder. For 3 and 5, the GCD is 1 (as 1 is the only common divisor).
Using the formula:
LCM(3, 5) = (|3 x 5|) / GCD(3, 5) = 15 / 1 = 15
This formula is efficient for larger numbers where finding the GCD is relatively easy using the Euclidean algorithm or prime factorization.
The Significance of LCMs
The concept of LCM isn't just an abstract mathematical exercise; it has practical applications in various areas:
-
Fraction Operations: Finding the LCM is crucial when adding or subtracting fractions with different denominators. The LCM of the denominators becomes the common denominator, simplifying the calculation. For example, adding 1/3 and 1/5 requires finding the LCM of 3 and 5 (which is 15), allowing us to rewrite the fractions as 5/15 and 3/15 respectively, simplifying the addition.
-
Scheduling Problems: LCM is vital in solving scheduling problems. Imagine two events occurring at regular intervals. Finding the LCM of those intervals helps determine when both events will occur simultaneously. For example, if one event happens every 3 days and another every 5 days, the LCM (15) indicates that both events will occur together every 15 days.
-
Cyclic Patterns: Many real-world phenomena exhibit cyclic patterns. Finding the LCM helps determine when these cycles will align. This is applicable in various fields like physics, engineering, and even music.
-
Modular Arithmetic: LCM plays a crucial role in modular arithmetic, a branch of number theory that deals with remainders after division. Understanding LCM is fundamental for solving congruence problems and other advanced mathematical concepts.
Beyond the Basics: Extending the Concept
The LCM concept extends beyond just two numbers. We can find the LCM of three or more numbers using similar methods, albeit with slightly more complexity. For instance, to find the LCM of 3, 5, and 7, we'd use prime factorization:
- 3 = 3
- 5 = 5
- 7 = 7
The LCM would be 3 x 5 x 7 = 105.
Frequently Asked Questions (FAQ)
Q: What if the two numbers share a common factor other than 1?
A: If the numbers share a common factor, the LCM will be smaller than simply multiplying the two numbers. The prime factorization method or the GCD formula effectively handles this scenario, ensuring you arrive at the least common multiple.
Q: Is there a limit to the size of numbers for which we can find the LCM?
A: Theoretically, there's no limit. While manual calculation becomes cumbersome for very large numbers, computers can easily handle the calculations using algorithms designed for finding LCMs and GCDs efficiently.
Q: How does the LCM relate to the GCD?
A: The LCM and GCD are inversely related. For two numbers a and b, the product of their LCM and GCD always equals the product of the two numbers: LCM(a, b) x GCD(a, b) = a x b. This relationship provides a useful check for your calculations.
Q: Why is the LCM important in everyday life?
A: While not explicitly used daily by most people, the principles behind LCM are used in numerous applications that affect daily life, from scheduling manufacturing processes to optimizing resource allocation in logistics and even syncing data in software systems. Understanding LCM provides a foundational understanding of these processes.
Conclusion
Finding the LCM of 3 and 5, while seemingly simple, serves as a gateway to understanding a fundamental concept in mathematics. Mastering the various methods—listing multiples, prime factorization, and using the GCD formula—provides a strong foundation for tackling more complex mathematical problems. The applications of LCM extend far beyond the classroom, highlighting its significance in various fields. By understanding the underlying principles and different calculation methods, you'll be well-equipped to handle LCM problems and appreciate its role in various applications. Remember, mathematics is not just about memorizing formulas; it's about understanding the underlying logic and applying it to solve real-world problems.
Latest Posts
Latest Posts
-
Bird In The Arabian Nights
Sep 21, 2025
-
Greek Word For The Sun
Sep 21, 2025
-
Is There Water In Oxygen
Sep 21, 2025
-
Top Bands Of The 60s
Sep 21, 2025
-
500 Ml In Pints Uk
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 3 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.