Integrate 1 2x 1 2
marihuanalabs
Sep 16, 2025 · 5 min read
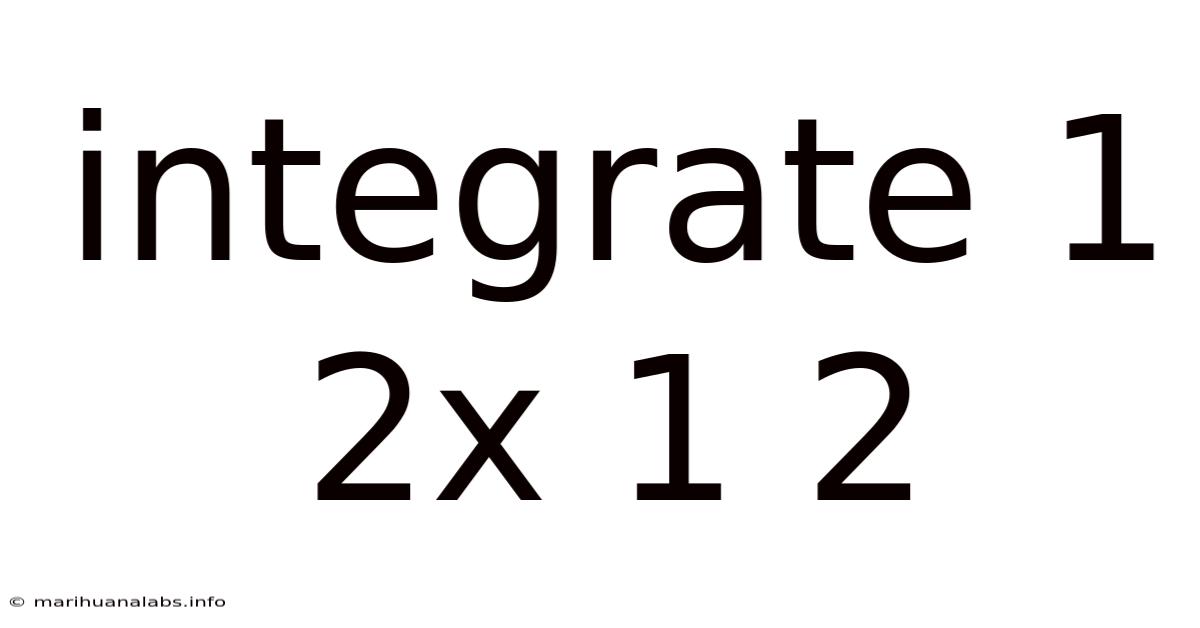
Table of Contents
Integrating 1/2 x 1/2: A Deep Dive into Fraction Multiplication and Beyond
Understanding how to multiply fractions is a fundamental concept in mathematics, crucial for progressing to more advanced topics like algebra, calculus, and beyond. This article will delve into the seemingly simple problem of integrating 1/2 x 1/2, exploring the underlying principles of fraction multiplication, providing practical examples, and extending the concept to more complex scenarios. We'll also address common misconceptions and frequently asked questions to ensure a thorough understanding. This guide aims to equip you with not just the answer, but a deep understanding of the why behind the calculation.
Understanding Fraction Multiplication: The Basics
Before tackling the specific problem of 1/2 x 1/2, let's establish the fundamental principles of multiplying fractions. The core concept is surprisingly straightforward: to multiply fractions, you simply multiply the numerators (top numbers) together and the denominators (bottom numbers) together.
For example, if we want to multiply 2/3 by 3/4, we would perform the following calculation:
(2/3) x (3/4) = (2 x 3) / (3 x 4) = 6/12
Notice that we multiplied the numerators (2 and 3) to get 6, and the denominators (3 and 4) to get 12. The resulting fraction, 6/12, can then be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 6 and 12 is 6, so we simplify 6/12 to 1/2.
This simple rule applies to all fraction multiplication problems, including our target problem: 1/2 x 1/2.
Solving 1/2 x 1/2: A Step-by-Step Approach
Now, let's apply the principles above to solve 1/2 x 1/2:
- Multiply the numerators: 1 x 1 = 1
- Multiply the denominators: 2 x 2 = 4
- Combine the results: The result is 1/4.
Therefore, 1/2 x 1/2 = 1/4. This result is already in its simplest form, as the GCD of 1 and 4 is 1.
Visualizing Fraction Multiplication: A Geometric Approach
Understanding fractions can sometimes be challenging, especially for visual learners. Let's visualize the multiplication of 1/2 x 1/2 using a geometric representation. Imagine a square with sides of length 1 unit.
- Divide the square in half: This represents 1/2.
- Divide one of the halves in half again: This represents taking 1/2 of the 1/2 we already have.
- Observe the result: The resulting area represents 1/4 of the original square.
This visual representation provides an intuitive understanding of why 1/2 x 1/2 equals 1/4. It shows that multiplying fractions involves finding a portion of a portion.
Extending the Concept: Multiplying More Than Two Fractions
The principles of fraction multiplication extend seamlessly to scenarios involving more than two fractions. We simply multiply all the numerators together and all the denominators together. For example:
(1/2) x (1/3) x (1/4) = (1 x 1 x 1) / (2 x 3 x 4) = 1/24
Again, we can simplify the resulting fraction if possible. In this case, 1/24 is already in its simplest form.
Dealing with Mixed Numbers: A Conversion Strategy
Sometimes, you might encounter mixed numbers (a whole number and a fraction) in multiplication problems. Before applying the fraction multiplication rules, it's essential to convert the mixed numbers into improper fractions (where the numerator is greater than or equal to the denominator).
For example, let's multiply 1 1/2 by 2/3:
- Convert 1 1/2 to an improper fraction: 1 1/2 = (1 x 2 + 1) / 2 = 3/2
- Multiply the fractions: (3/2) x (2/3) = (3 x 2) / (2 x 3) = 6/6 = 1
This illustrates that even with mixed numbers, the fundamental principles of fraction multiplication remain the same.
Applications of Fraction Multiplication: Real-World Examples
Fraction multiplication isn't just a theoretical concept; it has numerous practical applications in everyday life. Some examples include:
- Cooking and baking: Scaling recipes up or down requires multiplying ingredient amounts by fractions.
- Construction and engineering: Calculating material quantities and dimensions often involves fraction multiplication.
- Finance: Determining percentages, calculating interest, and dividing assets often involve fractional calculations.
- Data analysis: Representing and manipulating proportions and probabilities frequently involves fractions.
Common Misconceptions and Errors
While fraction multiplication is relatively straightforward, some common misconceptions can lead to errors:
- Confusing multiplication with addition: Remember that multiplying fractions is different from adding them. You multiply numerators and denominators separately, not add them.
- Forgetting to simplify: Always simplify the resulting fraction to its lowest terms to obtain the most accurate and concise answer.
- Incorrectly converting mixed numbers: Ensure you correctly convert mixed numbers to improper fractions before performing the multiplication.
Frequently Asked Questions (FAQ)
Q1: Can I multiply fractions with different denominators?
A1: Yes, absolutely. The rules of fraction multiplication apply regardless of whether the denominators are the same or different.
Q2: What if one of the fractions is a whole number?
A2: Treat the whole number as a fraction with a denominator of 1. For example, 3 x (1/2) = (3/1) x (1/2) = 3/2 = 1 1/2.
Q3: Is there a way to estimate the result of fraction multiplication before calculating it?
A3: Yes, you can get a rough estimate by rounding the fractions to the nearest whole number or easily manageable fraction. This helps to check the reasonableness of your final answer.
Q4: How can I improve my skills in fraction multiplication?
A4: Practice regularly with various problems. Start with simple problems and gradually increase the complexity. Use visual aids and real-world examples to reinforce your understanding.
Conclusion: Mastering Fraction Multiplication
Integrating 1/2 x 1/2, while seemingly simple, serves as a gateway to understanding the broader concept of fraction multiplication. This fundamental skill is crucial for numerous mathematical applications and real-world scenarios. By mastering the principles outlined in this article, along with consistent practice, you can build a strong foundation in mathematics and confidently tackle more complex problems. Remember, the key lies in understanding the underlying why behind the calculation, not just memorizing the procedure. This approach will enhance your problem-solving skills and provide a deeper appreciation for the beauty and elegance of mathematics.
Latest Posts
Latest Posts
-
84 Months How Many Years
Sep 16, 2025
-
Making An Effective Decision Example
Sep 16, 2025
-
Lewis Dot Structure For Water
Sep 16, 2025
-
Holding The Line Barbara Kingsolver
Sep 16, 2025
-
Semi Variable Cost With Example
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Integrate 1 2x 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.