Integral Of 1 1 2x
marihuanalabs
Sep 23, 2025 · 5 min read
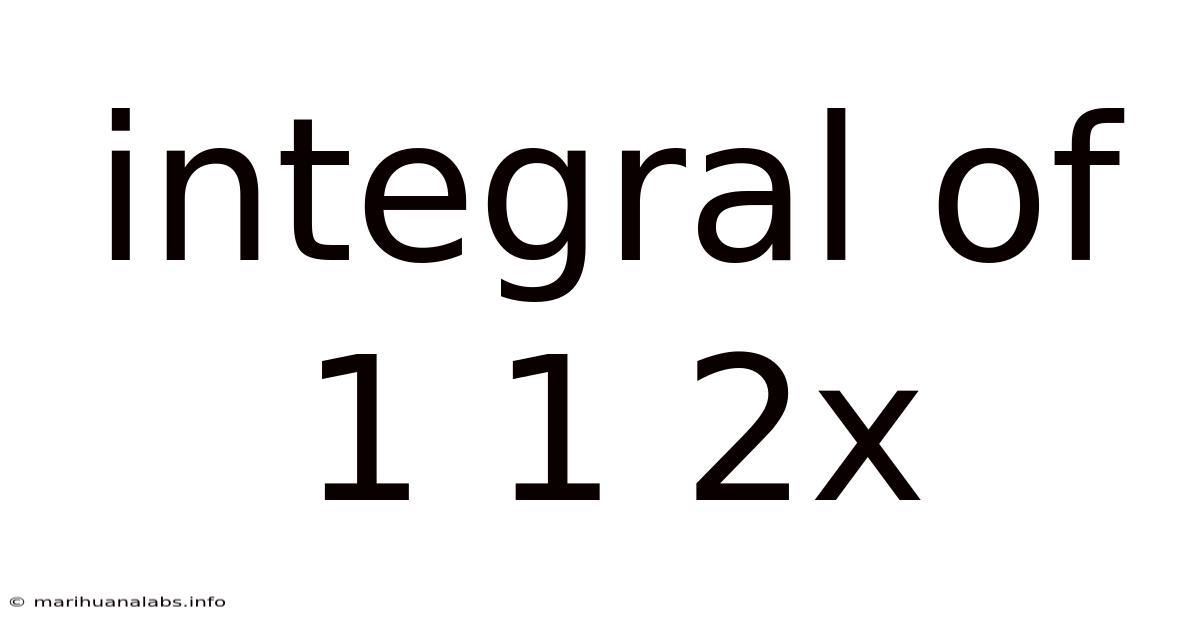
Table of Contents
Understanding and Solving the Integral of 1/(1+2x)
The integral ∫1/(1+2x) dx might seem deceptively simple at first glance, but it serves as an excellent example to illustrate several key concepts in integral calculus. This article will guide you through the process of solving this integral, explaining the underlying principles and offering insights for tackling similar problems. We'll explore different methods, delve into the underlying theory, and address frequently asked questions. This comprehensive guide aims to equip you with a solid understanding, not just of this specific integral, but of integration techniques in general.
Introduction: A Primer on Integration
Integration is essentially the reverse process of differentiation. While differentiation finds the instantaneous rate of change of a function, integration finds the function whose derivative is the given function. The integral ∫f(x) dx represents the indefinite integral of f(x) – meaning we're finding a family of functions whose derivatives are f(x). We'll add a constant of integration, 'C', to account for this family of solutions. The definite integral, on the other hand, ∫<sub>a</sub><sup>b</sup> f(x) dx, calculates the area under the curve of f(x) between the limits a and b.
Our focus here is on the indefinite integral ∫1/(1+2x) dx. We'll use the method of u-substitution, a powerful technique for simplifying integrals.
Step-by-Step Solution using u-Substitution
The key to solving this integral lies in recognizing that the denominator (1+2x) presents a challenge. The u-substitution method helps us overcome this.
1. Choosing the 'u':
Let's choose u = 1 + 2x. This is a strategic choice because the derivative of u with respect to x is du/dx = 2. This derivative will neatly cancel out a factor in the original integral.
2. Finding du:
From du/dx = 2, we can rearrange to find du = 2dx. This gives us a direct substitution for 'dx' in the integral.
3. Substituting into the Integral:
Now, let's substitute u for (1+2x) and du/2 for dx into our original integral:
∫1/(1+2x) dx = ∫1/u (du/2)
4. Simplifying and Integrating:
The integral simplifies to:
(1/2) ∫1/u du
This is a much simpler integral to solve. The integral of 1/u with respect to u is ln|u| (the natural logarithm of the absolute value of u). Remember the absolute value is crucial to ensure the logarithm is defined for both positive and negative values of u.
Therefore, our integration yields:
(1/2) ln|u| + C
5. Substituting Back:
Finally, we substitute back our original expression for u (u = 1 + 2x) to express the solution in terms of x:
(1/2) ln|1 + 2x| + C
Thus, the solution to the integral ∫1/(1+2x) dx is (1/2)ln|1 + 2x| + C.
A Deeper Dive: Understanding the ln|u| Result
The appearance of the natural logarithm in the solution isn't accidental. The natural logarithm is the antiderivative (integral) of 1/x. This relationship stems from the fundamental theorem of calculus and the properties of exponential and logarithmic functions. The absolute value is included because the natural logarithm is only defined for positive arguments.
Alternative Approaches and Considerations
While u-substitution is the most straightforward method for this particular integral, let's briefly consider other approaches and nuances.
-
Direct Integration (Less Efficient): While possible to manipulate the integral without u-substitution, it would be significantly more complex and less intuitive. It would involve techniques less commonly used in elementary calculus.
-
Definite Integrals: If this were a definite integral (e.g., ∫<sub>0</sub><sup>1</sup> 1/(1+2x) dx), the process would remain similar, but the final step would involve evaluating the antiderivative at the upper and lower limits of integration and finding the difference.
Expanding the Understanding: Related Integrals
Understanding this integral opens the door to tackling more complex problems. The principles of u-substitution can be extended to integrals of the form ∫1/(ax+b) dx, where 'a' and 'b' are constants. Following a similar approach, the solution for this general form is (1/a)ln|ax+b| + C.
Frequently Asked Questions (FAQs)
Q1: Why is the absolute value sign necessary in the final answer?
The natural logarithm function is only defined for positive arguments. The absolute value ensures that the argument of the logarithm is always positive, regardless of the value of x. This expands the domain of the antiderivative to include both positive and negative values of (1+2x).
Q2: What if the numerator was different? For example, ∫x/(1+2x) dx?
This requires a different approach. You would likely need to perform polynomial long division or adjust your u-substitution strategy to handle the 'x' in the numerator. Polynomial long division would allow you to rewrite the integrand as a sum of a polynomial and a simpler rational function, making integration easier.
Q3: Can this integral be solved using integration by parts?
Integration by parts is generally used for integrals involving products of functions. While technically possible to apply it, it would be overly complicated and less efficient than u-substitution in this scenario. U-substitution is the more straightforward and elegant solution.
Q4: What is the significance of the constant of integration, C?
The constant of integration, C, represents the family of antiderivatives. Since the derivative of a constant is zero, adding any constant to the antiderivative doesn't change its derivative. Therefore, we include 'C' to account for all possible antiderivatives that would satisfy the original integral.
Q5: How can I check my answer?
You can verify your solution by differentiating the result. The derivative of (1/2)ln|1 + 2x| + C should equal 1/(1+2x), the original integrand. This is a crucial step to confirm the accuracy of your integration.
Conclusion: Mastering Integration Techniques
Solving the integral ∫1/(1+2x) dx is not only about obtaining the correct answer – (1/2)ln|1 + 2x| + C – but about understanding the underlying principles of integration. This simple integral serves as a valuable stepping stone to mastering more complex integration techniques. The method of u-substitution, demonstrated here, is a fundamental tool in your calculus toolkit, enabling you to simplify and solve a wide range of integration problems. Remember to practice regularly and explore diverse problems to build your confidence and proficiency. The more you work through examples and understand the underlying logic, the more intuitive integration will become.
Latest Posts
Latest Posts
-
Gcf Of 98 And 42
Sep 23, 2025
-
Brave New World Book Cover
Sep 23, 2025
-
What Is A Humiliation Ritual
Sep 23, 2025
-
Features Of A Letter Ks1
Sep 23, 2025
-
Can Botox Cause Bells Palsy
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 1 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.