Hcf Of 60 And 84
marihuanalabs
Sep 21, 2025 · 6 min read
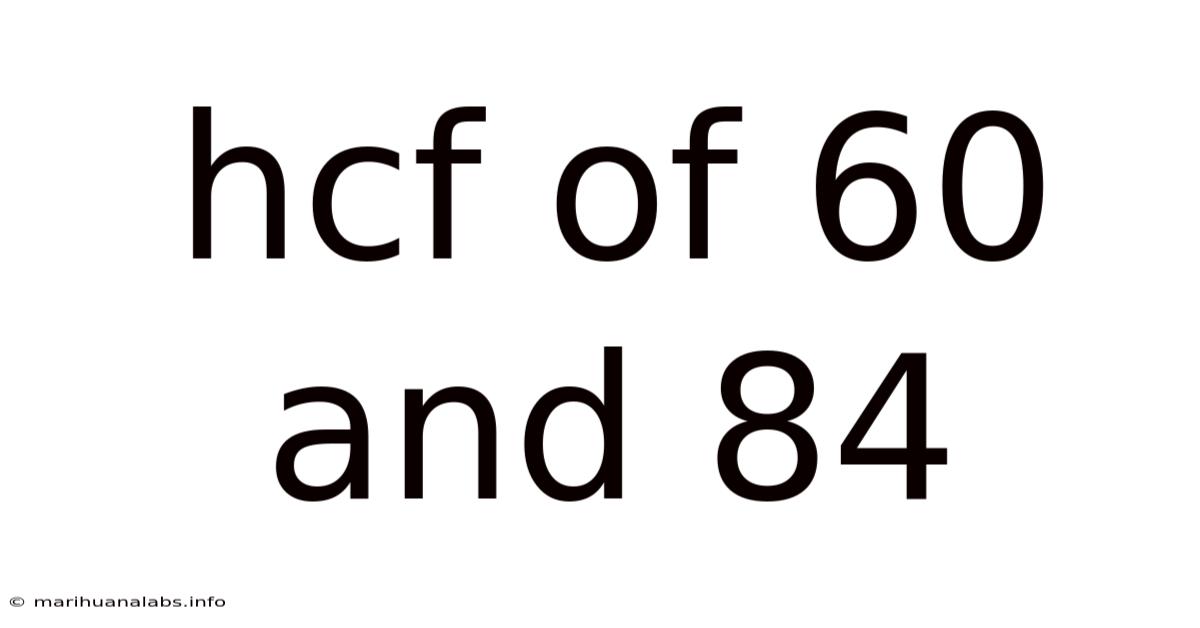
Table of Contents
Finding the Highest Common Factor (HCF) of 60 and 84: A Comprehensive Guide
Finding the highest common factor (HCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This article will delve deep into the process of calculating the HCF of 60 and 84, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll cover everything from basic prime factorization to more advanced techniques, ensuring you gain a solid grasp of this important mathematical skill. Understanding HCF is crucial for simplifying fractions, solving algebraic problems, and laying the groundwork for more advanced mathematical concepts.
Introduction: What is the Highest Common Factor (HCF)?
The highest common factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers exactly. For example, the HCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder. This seemingly simple concept has wide-ranging applications in various mathematical fields. This article will focus specifically on finding the HCF of 60 and 84, using several different approaches to illustrate the versatility of the concept.
Method 1: Prime Factorization
This is a classic and widely used method for determining the HCF. It involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves.
Steps:
-
Find the prime factorization of 60: 60 = 2 x 2 x 3 x 5 = 2² x 3 x 5
-
Find the prime factorization of 84: 84 = 2 x 2 x 3 x 7 = 2² x 3 x 7
-
Identify common prime factors: Both 60 and 84 share the prime factors 2² and 3.
-
Calculate the HCF: Multiply the common prime factors together. In this case, the HCF is 2² x 3 = 4 x 3 = 12.
Therefore, the HCF of 60 and 84 is 12.
This method is particularly helpful for understanding the fundamental structure of numbers and their divisibility. It provides a clear visual representation of the factors involved.
Method 2: Listing Factors
This method is simpler for smaller numbers but can become cumbersome for larger ones.
Steps:
-
List all factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
-
List all factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
-
Identify common factors: Compare the two lists and find the numbers that appear in both. The common factors are 1, 2, 3, 4, 6, and 12.
-
Determine the HCF: The largest number among the common factors is 12.
Therefore, the HCF of 60 and 84 is 12.
This method, although straightforward, can be less efficient for larger numbers, highlighting the benefits of more advanced techniques.
Method 3: Euclidean Algorithm
The Euclidean Algorithm is a highly efficient method for finding the HCF, especially for larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the HCF.
Steps:
-
Start with the larger number (84) and the smaller number (60).
-
Divide the larger number by the smaller number and find the remainder: 84 ÷ 60 = 1 with a remainder of 24.
-
Replace the larger number with the smaller number (60) and the smaller number with the remainder (24).
-
Repeat the division process: 60 ÷ 24 = 2 with a remainder of 12.
-
Repeat again: 24 ÷ 12 = 2 with a remainder of 0.
-
The HCF is the last non-zero remainder. In this case, the last non-zero remainder is 12.
Therefore, the HCF of 60 and 84 is 12.
The Euclidean Algorithm is significantly more efficient than the listing factors method for larger numbers, making it a preferred approach in many computational scenarios.
Understanding the Significance of the HCF
The HCF of 60 and 84, being 12, has several important implications:
-
Fraction Simplification: If you have a fraction with 60 as the numerator and 84 as the denominator (60/84), you can simplify it by dividing both the numerator and the denominator by their HCF (12). This simplifies the fraction to 5/7, its simplest form.
-
Problem Solving: Many mathematical problems, especially those involving ratios, proportions, and divisibility, rely on finding the HCF to arrive at a solution.
-
Geometry: The concept of HCF is applied in geometrical problems involving finding the dimensions of squares or rectangles that can be formed from a given area.
Extending the Concept: HCF of More Than Two Numbers
The methods described above can be extended to find the HCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors to the lowest power. For the Euclidean algorithm, you would repeatedly apply the algorithm to pairs of numbers until you arrive at a single common divisor.
Frequently Asked Questions (FAQ)
Q1: What if the HCF of two numbers is 1?
A1: If the HCF of two numbers is 1, the numbers are said to be relatively prime or coprime. This means they share no common factors other than 1.
Q2: Can the HCF of two numbers be greater than the smaller number?
A2: No. The HCF can never be greater than the smaller of the two numbers. By definition, the HCF must divide both numbers without leaving a remainder.
Q3: Are there any other methods to find the HCF?
A3: Yes, there are more advanced algorithms like the binary GCD algorithm, which is optimized for computer calculations. However, the methods described above are sufficient for most practical purposes.
Q4: Why is understanding HCF important?
A4: Understanding HCF is crucial for simplifying fractions, solving problems involving ratios and proportions, and laying the foundation for more advanced mathematical concepts such as modular arithmetic and abstract algebra.
Conclusion: Mastering the HCF
Finding the highest common factor is a fundamental skill in mathematics with broad applications. This article has explored various methods for calculating the HCF of 60 and 84, highlighting the advantages and disadvantages of each approach. Whether you use prime factorization, listing factors, or the Euclidean algorithm, the core concept remains the same: identifying the largest number that divides both numbers without leaving a remainder. Understanding and mastering this concept will significantly enhance your mathematical abilities and problem-solving skills. Remember to choose the method that best suits the numbers you're working with – for smaller numbers, listing factors might be sufficient, while for larger numbers, the Euclidean algorithm provides a more efficient approach. The key is to practice and become comfortable with these methods to confidently tackle various mathematical challenges involving HCF.
Latest Posts
Latest Posts
-
Quotes From Emilia In Othello
Sep 21, 2025
-
Map Of Mountain Ranges Uk
Sep 21, 2025
-
Lush Shoot For The Stars
Sep 21, 2025
-
Limitations Of The Cognitive Approach
Sep 21, 2025
-
Adjectives Beginning With An S
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 60 And 84 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.