Graph Y 1 2x 2
marihuanalabs
Sep 20, 2025 · 6 min read
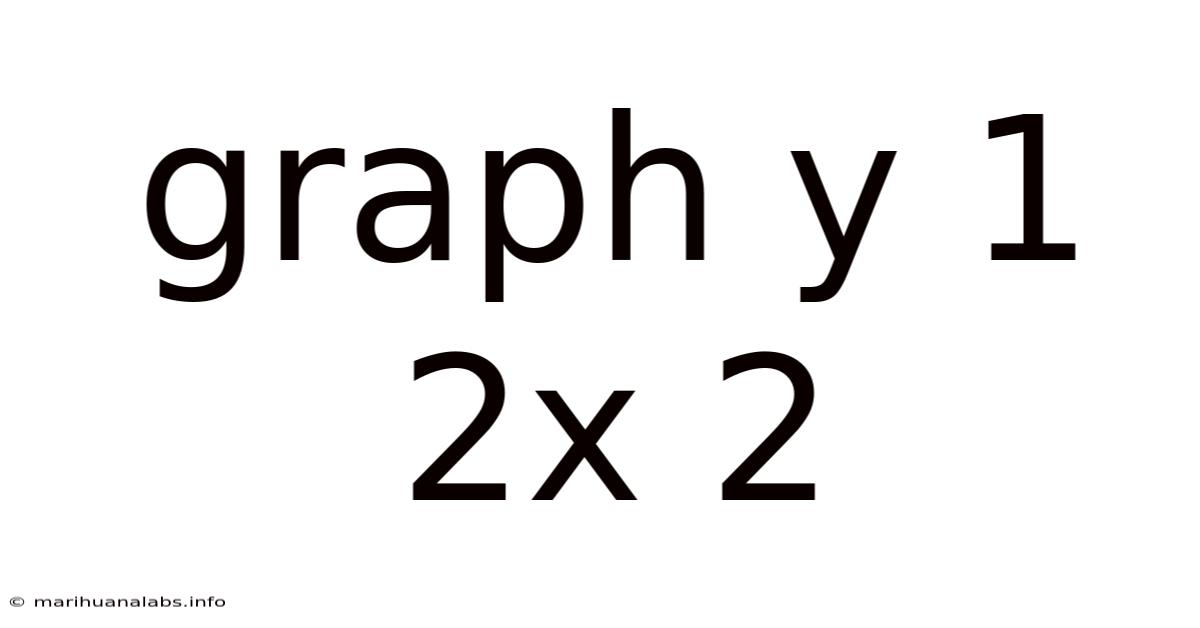
Table of Contents
Understanding the Linear Equation: y = 1/2x + 2
This article delves into the linear equation y = 1/2x + 2, exploring its components, graphing techniques, interpretations, and real-world applications. We'll cover everything from basic understanding to more advanced concepts, making it accessible for students of all levels. By the end, you'll not only be able to graph this equation but also understand its significance within the broader context of algebra and beyond.
Introduction: Deconstructing the Equation
The equation y = 1/2x + 2 represents a linear equation in slope-intercept form. This form, often written as y = mx + b, provides a concise way to represent a straight line on a Cartesian coordinate plane. Let's break down each component:
- y: Represents the dependent variable. Its value depends on the value of x.
- x: Represents the independent variable. We choose values for x, and the equation calculates the corresponding y value.
- m (1/2): Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope (like ours) means the line rises from left to right. The value 1/2 signifies that for every 2 units increase in x, y increases by 1 unit. This can also be expressed as a rise of 1 and a run of 2.
- b (2): Represents the y-intercept. This is the point where the line crosses the y-axis (where x = 0). In our equation, the y-intercept is 2, meaning the line passes through the point (0, 2).
Graphing y = 1/2x + 2: A Step-by-Step Guide
Graphing this linear equation is straightforward. We can utilize two primary methods:
Method 1: Using the Slope and Y-intercept
-
Plot the y-intercept: Start by plotting the point (0, 2) on the Cartesian plane. This is our starting point.
-
Use the slope to find another point: The slope is 1/2. This means a "rise" of 1 and a "run" of 2. From the y-intercept (0, 2), move 1 unit up (rise) and 2 units to the right (run). This brings us to the point (2, 3).
-
Plot the second point and draw the line: Plot the point (2, 3). Now, draw a straight line that passes through both points (0, 2) and (2, 3). This line represents the graph of y = 1/2x + 2.
Method 2: Using a Table of Values
This method involves creating a table with various x-values and calculating their corresponding y-values using the equation.
| x | y = 1/2x + 2 | (x, y) coordinates |
|---|---|---|
| -4 | 0 | (-4, 0) |
| -2 | 1 | (-2, 1) |
| 0 | 2 | (0, 2) |
| 2 | 3 | (2, 3) |
| 4 | 4 | (4, 4) |
-
Choose x-values: Select a range of x-values, including both positive and negative numbers.
-
Calculate y-values: Substitute each x-value into the equation y = 1/2x + 2 to calculate the corresponding y-value.
-
Plot the points: Plot the (x, y) coordinate pairs from the table on the Cartesian plane.
-
Draw the line: Draw a straight line that passes through all the plotted points. This line represents the graph of y = 1/2x + 2. You'll notice that both methods produce the same line.
Interpreting the Graph
The graph of y = 1/2x + 2 provides valuable information:
-
Linear Relationship: The straight line indicates a linear relationship between x and y. This means that as x increases, y increases proportionally.
-
Rate of Change: The slope (1/2) represents the rate of change of y with respect to x. For every unit increase in x, y increases by 0.5 units.
-
Y-intercept: The y-intercept (2) represents the value of y when x is 0. This could represent an initial value or a starting point in a real-world context.
-
Predictive Power: The equation and its graph allow us to predict the value of y for any given x-value, and vice-versa.
Real-World Applications
Linear equations like y = 1/2x + 2 have numerous real-world applications:
-
Cost Calculations: Imagine a taxi fare where the initial charge is $2 (y-intercept) and the cost per mile is $0.50 (slope). The equation would then represent the total cost (y) based on the number of miles traveled (x).
-
Distance-Time Relationships: Consider a cyclist traveling at a constant speed. If the cyclist starts 2 kilometers from a certain point and travels at 0.5 kilometers per hour, the equation could model the distance from the starting point over time.
-
Simple Interest: In basic finance, simple interest can be modeled using a linear equation, where the initial principal is the y-intercept, and the interest rate per period is the slope.
-
Scientific Modeling: Many scientific phenomena can be approximated by linear relationships, especially over small ranges of values.
Beyond the Basics: Exploring Related Concepts
Understanding y = 1/2x + 2 opens doors to more advanced concepts:
-
Finding the x-intercept: The x-intercept is the point where the line crosses the x-axis (where y = 0). To find it, set y = 0 in the equation and solve for x: 0 = 1/2x + 2; x = -4. The x-intercept is (-4, 0).
-
Parallel and Perpendicular Lines: Any line with a slope of 1/2 will be parallel to y = 1/2x + 2. A line perpendicular to y = 1/2x + 2 will have a slope that is the negative reciprocal of 1/2, which is -2.
-
Systems of Equations: We can use this equation in conjunction with other linear equations to find the point of intersection, which represents a solution to the system.
-
Inequalities: We can extend this to linear inequalities, such as y > 1/2x + 2 or y ≤ 1/2x + 2, which represent regions on the coordinate plane rather than just a single line.
Frequently Asked Questions (FAQ)
Q: What does the slope of 1/2 mean in practical terms?
A: The slope of 1/2 indicates that for every 2 units of increase in the x-value, the y-value increases by 1 unit. It represents the rate of change between the two variables.
Q: How can I find the x-intercept?
A: To find the x-intercept, set y = 0 and solve the equation for x. In this case, 0 = 1/2x + 2, which gives x = -4. The x-intercept is (-4,0).
Q: What if the equation was y = -1/2x + 2? How would the graph change?
A: The graph would still have a y-intercept of 2, but the slope would be negative (-1/2). This means the line would slope downwards from left to right, indicating an inverse relationship between x and y.
Q: Can this equation be used to model any real-world situation?
A: While not every situation is perfectly linear, many can be approximated using linear equations over a limited range. This makes linear equations a powerful tool for modeling and prediction.
Conclusion: A Foundation for Further Learning
The seemingly simple equation y = 1/2x + 2 provides a solid foundation for understanding linear equations, graphing techniques, and their applications. By mastering this foundational concept, you'll be well-prepared to tackle more complex algebraic concepts and apply your knowledge to various real-world problems. Remember, the key is not just memorizing the steps but understanding the underlying principles and their implications. Continue exploring, ask questions, and practice – your mathematical skills will flourish!
Latest Posts
Latest Posts
-
Words That Finish With Able
Sep 20, 2025
-
J Adore Meaning In English
Sep 20, 2025
-
Passed Of Time Crossword Clue
Sep 20, 2025
-
What Is 75grams In Ounces
Sep 20, 2025
-
Particular Solutions For Differential Equations
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Graph Y 1 2x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.