Factorise 3x 2 5x 12
marihuanalabs
Sep 23, 2025 · 6 min read
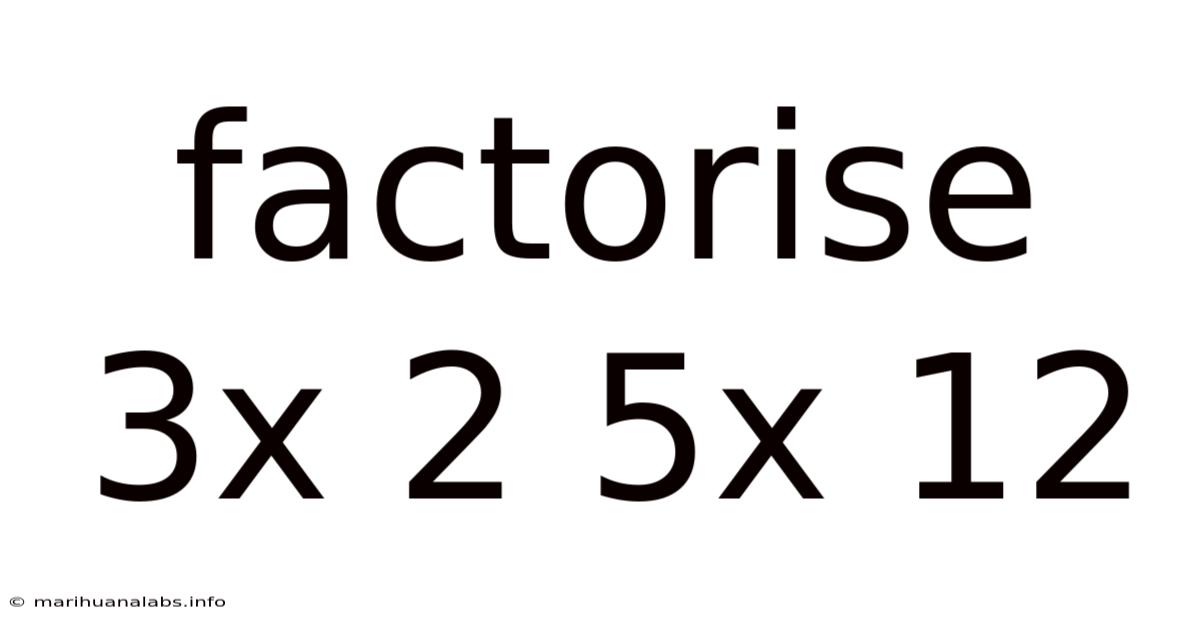
Table of Contents
Factorising Quadratic Expressions: A Deep Dive into 3x² + 5x - 12
Factorising quadratic expressions is a fundamental skill in algebra. Understanding how to factorise allows you to simplify equations, solve for unknowns, and delve deeper into the behaviour of polynomial functions. This article provides a comprehensive guide to factorising the quadratic expression 3x² + 5x - 12, explaining the process step-by-step and exploring the underlying mathematical principles. We'll also delve into different methods and address frequently asked questions.
Understanding Quadratic Expressions
Before we tackle the factorisation of 3x² + 5x - 12, let's establish a foundation. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. In our example, 3x² + 5x - 12, we have a = 3, b = 5, and c = -12.
Factorising a quadratic expression means rewriting it as a product of two linear expressions. This is crucial for solving quadratic equations (where the expression equals zero) and simplifying more complex algebraic expressions.
Method 1: The AC Method
The AC method, also known as the splitting the middle term method, is a systematic approach to factorising quadratic expressions. Here's how it works for 3x² + 5x - 12:
-
Find the product AC: Multiply the coefficient of the x² term (a) by the constant term (c): 3 * (-12) = -36.
-
Find two numbers that add up to B and multiply to AC: We need two numbers that add up to 5 (the coefficient of the x term, b) and multiply to -36. These numbers are 9 and -4 (9 + (-4) = 5 and 9 * (-4) = -36).
-
Rewrite the middle term: Rewrite the middle term (5x) using the two numbers we found: 3x² + 9x - 4x - 12.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- 3x(x + 3) - 4(x + 3)
-
Factor out the common binomial: Notice that (x + 3) is a common factor in both terms. Factor it out: (x + 3)(3x - 4).
Therefore, the factorised form of 3x² + 5x - 12 is (x + 3)(3x - 4).
Method 2: Trial and Error
This method involves a bit of guesswork, but it can be faster once you gain experience. We need to find two binomials that multiply to give 3x² + 5x - 12. We know that the first terms in the binomials must multiply to 3x², so they could be 3x and x. The last terms must multiply to -12. Possible pairs of factors of -12 are:
- (1, -12), (-1, 12), (2, -6), (-2, 6), (3, -4), (-3, 4)
We try different combinations until we find one that gives the correct middle term (5x):
Let's try (3x + 4)(x - 3): This expands to 3x² - 9x + 4x - 12 = 3x² - 5x - 12 (Incorrect) Let's try (3x - 4)(x + 3): This expands to 3x² + 9x - 4x - 12 = 3x² + 5x - 12 (Correct!)
So, again, the factorised form is (3x - 4)(x + 3). Note that the order of the factors doesn't matter since multiplication is commutative.
Method 3: Using the Quadratic Formula (Indirect Factorisation)
While not a direct factorisation method, the quadratic formula can help find the roots of the quadratic equation 3x² + 5x - 12 = 0. These roots can then be used to construct the factored form. The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Plugging in our values (a = 3, b = 5, c = -12):
x = [-5 ± √(5² - 4 * 3 * -12)] / (2 * 3) x = [-5 ± √(25 + 144)] / 6 x = [-5 ± √169] / 6 x = [-5 ± 13] / 6
This gives us two solutions:
x₁ = (-5 + 13) / 6 = 8/6 = 4/3 x₂ = (-5 - 13) / 6 = -18/6 = -3
These are the roots of the quadratic equation. To find the factors, we use the fact that if r is a root, then (x - r) is a factor. Therefore, our factors are (x - 4/3) and (x + 3). To get rid of the fraction, we can multiply (x - 4/3) by 3: 3(x - 4/3) = 3x - 4.
Thus, the factored form is (3x - 4)(x + 3).
Verifying the Factorisation
To ensure our factorisation is correct, we can expand the factored form:
(3x - 4)(x + 3) = 3x² + 9x - 4x - 12 = 3x² + 5x - 12
This matches our original quadratic expression, confirming that our factorisation is accurate.
Solving Quadratic Equations using Factorisation
Once we have factorised the quadratic expression, we can use it to solve the corresponding quadratic equation, 3x² + 5x - 12 = 0.
Since (3x - 4)(x + 3) = 0, either (3x - 4) = 0 or (x + 3) = 0. This gives us two solutions:
- 3x - 4 = 0 => 3x = 4 => x = 4/3
- x + 3 = 0 => x = -3
Therefore, the solutions to the equation 3x² + 5x - 12 = 0 are x = 4/3 and x = -3. These are the roots or zeros of the quadratic equation.
The Significance of Factorisation
Factorising quadratic expressions is not merely a procedural exercise; it's a powerful tool with broad applications:
- Solving Quadratic Equations: As demonstrated, factorisation provides a direct method for finding the solutions to quadratic equations.
- Simplifying Algebraic Expressions: Factorisation allows you to simplify complex algebraic expressions, making them easier to manipulate and understand.
- Graphing Quadratic Functions: The factorised form reveals the x-intercepts (roots) of the quadratic function, which are crucial for accurately sketching its graph.
- Further Algebraic Manipulation: Factorised expressions are easier to work with when performing operations like division, cancellation, and simplification within more complex equations.
Frequently Asked Questions (FAQ)
Q: What if I can't find the two numbers that add up to 'b' and multiply to 'ac'?
A: If you can't find such numbers using the AC method, it's possible that the quadratic expression is not factorisable using integers. In such cases, you might need to use the quadratic formula to find the roots and then construct the factors, or accept that the quadratic expression is prime (cannot be factorised into simpler expressions with integer coefficients).
Q: Is there only one way to factorise a quadratic expression?
A: No. The order of the factors doesn't matter. (3x - 4)(x + 3) is the same as (x + 3)(3x - 4).
Q: What if the coefficient of x² is 1?
A: If a = 1 (e.g., x² + 5x + 6), the factorisation process simplifies. You just need to find two numbers that add up to the coefficient of x and multiply to the constant term. For x² + 5x + 6, those numbers are 2 and 3, so the factored form is (x + 2)(x + 3).
Q: Can I use the AC method for higher-degree polynomials?
A: While the AC method is primarily designed for quadratic expressions, similar principles of grouping and factoring can be applied to some higher-degree polynomials, although the process becomes more complex.
Conclusion
Factorising quadratic expressions, such as 3x² + 5x - 12, is a vital algebraic skill. The AC method, trial and error, and even the indirect use of the quadratic formula provide reliable ways to achieve this. Understanding the underlying principles and mastering these techniques will enhance your ability to solve equations, simplify expressions, and grasp deeper concepts in algebra and beyond. Remember to practice regularly to build confidence and speed in your factorisation skills. The more you practice, the easier it will become to recognise patterns and apply the most efficient method.
Latest Posts
Latest Posts
-
Church Of Christ Near Me
Sep 23, 2025
-
Super Human Beings Crossword 7
Sep 23, 2025
-
58 Degrees F To C
Sep 23, 2025
-
Jones English Architect Crossword Clue
Sep 23, 2025
-
Paintings Of The 19th Century
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Factorise 3x 2 5x 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.