Decrease 67 By 26 Percent
marihuanalabs
Sep 23, 2025 · 5 min read
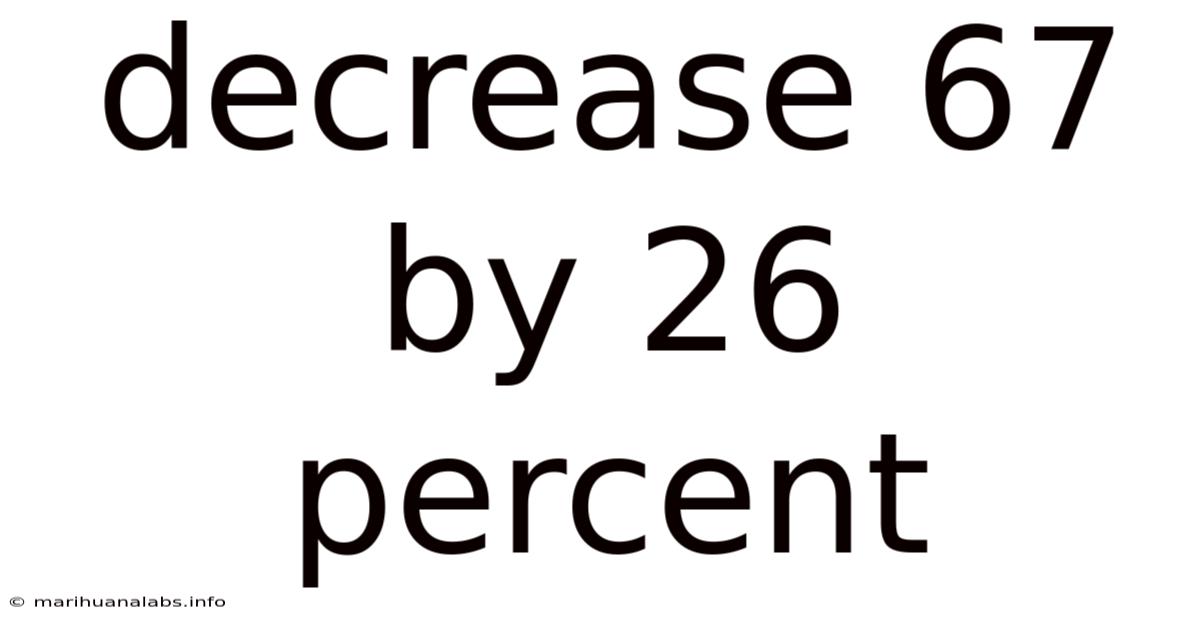
Table of Contents
Deconstructing Percentage Decrease: A Deep Dive into Reducing 67 by 26%
Understanding percentage decreases is a fundamental skill in mathematics with applications spanning various fields, from finance and budgeting to scientific analysis and everyday life. This article provides a comprehensive guide to calculating a percentage decrease, using the example of decreasing 67 by 26%. We will explore multiple approaches, delve into the underlying concepts, and address frequently asked questions, ensuring a thorough understanding of this crucial mathematical operation.
Introduction: Understanding Percentage Decrease
A percentage decrease represents the reduction of a quantity by a certain percentage. It's essentially finding a fraction of the original number and subtracting that fraction from the original value. In our case, we need to reduce 67 by 26%. This means finding 26% of 67 and then subtracting this value from 67. While the specific numbers may seem simple, understanding the underlying process is crucial for tackling more complex percentage decrease problems. This knowledge will empower you to confidently calculate discounts, analyze data, and solve real-world problems involving proportional changes.
Method 1: The Direct Approach – Calculating 26% of 67 and Subtracting
This is the most straightforward method. We first calculate 26% of 67 and then subtract the result from 67.
-
Calculate 26% of 67: To find 26% of 67, we convert the percentage to a decimal by dividing by 100: 26% = 26/100 = 0.26. Then, we multiply this decimal by 67: 0.26 * 67 = 17.42
-
Subtract from the original value: Now, subtract the calculated value (17.42) from the original number (67): 67 - 17.42 = 49.58
Therefore, decreasing 67 by 26% results in 49.58.
Method 2: The Multiplier Approach – A More Efficient Method
This method utilizes the concept that if you decrease a number by 26%, you are left with 74% (100% - 26%) of the original number. This approach simplifies the calculation.
-
Calculate the remaining percentage: Since we are decreasing by 26%, the remaining percentage is 100% - 26% = 74%.
-
Convert the percentage to a decimal: Convert 74% to a decimal: 74% = 74/100 = 0.74
-
Multiply the original value by the decimal: Multiply the original number (67) by the decimal (0.74): 0.74 * 67 = 49.58
This method yields the same result: 49.58. It's generally more efficient, especially when dealing with multiple percentage decrease calculations.
Method 3: Using Fractions – A Fundamental Approach
This method uses the fractional equivalent of the percentage. It reinforces the fundamental understanding of percentages as fractions.
-
Convert the percentage to a fraction: 26% can be written as the fraction 26/100, which simplifies to 13/50.
-
Calculate the decrease: Multiply the original number (67) by the fraction representing the decrease (13/50): (13/50) * 67 = 17.42
-
Subtract the decrease from the original value: Subtract the calculated decrease (17.42) from the original number (67): 67 - 17.42 = 49.58
Once again, the result is 49.58. This method highlights the connection between percentages, decimals, and fractions.
Explanation of the Underlying Mathematical Principles
The core concept behind percentage decrease lies in the understanding of proportions. A percentage is essentially a fraction out of 100. When we calculate 26% of 67, we're finding 26 parts out of 100 parts of 67. This fraction (26/100 or 0.26) represents the proportional decrease. Subtracting this proportional decrease from the original value gives the final result after the decrease.
The multiplier approach leverages the fact that if we're decreasing by 26%, we retain 74% of the original value. This 'remaining percentage' acts as a multiplier, directly providing the final value after the decrease. This is a highly efficient technique for percentage calculations.
Illustrative Real-World Examples
Percentage decrease is applicable in numerous real-world situations:
-
Sales Discounts: A store offers a 26% discount on an item originally priced at $67. The discounted price can be calculated using the methods described above.
-
Population Decline: A town's population decreases by 26% from an initial population of 67,000. The methods would allow us to calculate the new population.
-
Investment Losses: An investment portfolio loses 26% of its initial value of $67,000. The remaining value can be calculated using the percentage decrease techniques.
-
Scientific Data Analysis: In various scientific experiments and data analysis, a reduction of a certain quantity by a percentage is often calculated and interpreted.
These examples illustrate the versatility and practical significance of understanding and calculating percentage decreases.
Frequently Asked Questions (FAQ)
-
What if I need to increase a number by a percentage instead of decreasing it? To increase a number by a percentage, you add the calculated percentage increase to the original number instead of subtracting it. For instance, to increase 67 by 26%, calculate 26% of 67 (17.42) and add it to 67 (67 + 17.42 = 84.42). Alternatively, you can use the multiplier approach (1 + 0.26 = 1.26) and multiply the original number by 1.26.
-
Can I use a calculator for these calculations? Absolutely! Calculators are highly useful for simplifying these calculations, particularly with larger numbers or more complex percentage changes.
-
What if the percentage is a decimal, such as 26.5%? The methods described above still apply. Simply convert the decimal percentage to a decimal (26.5% = 0.265) and proceed with the calculations.
-
How can I check my answer? You can check your answer by reversing the process. Add the decrease amount (17.42) back to the final result (49.58) to see if it equals the original number (67).
Conclusion: Mastering Percentage Decrease
Calculating a percentage decrease, like reducing 67 by 26%, is a fundamental mathematical operation with wide-ranging applications. Mastering the various methods, from the direct approach to the more efficient multiplier method and the foundational fractional method, equips you with the skills to solve a variety of real-world problems involving proportional changes. Understanding the underlying mathematical principles provides a solid foundation for tackling more complex scenarios and reinforces your overall mathematical understanding. Remember to practice these methods to build confidence and proficiency in this crucial skill. By applying these methods and understanding the underlying principles, you’ll be well-equipped to confidently tackle any percentage decrease calculation you encounter. This knowledge is a valuable asset in various aspects of life, from personal finance to professional endeavors.
Latest Posts
Latest Posts
-
What Is An Overt Observation
Sep 23, 2025
-
Case Study Strengths And Weaknesses
Sep 23, 2025
-
House Of Lancaster Family Tree
Sep 23, 2025
-
7 To The 3rd Power
Sep 23, 2025
-
Story In Third Person Example
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Decrease 67 By 26 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.