Cos 2 Sin 2 1
marihuanalabs
Sep 15, 2025 · 6 min read
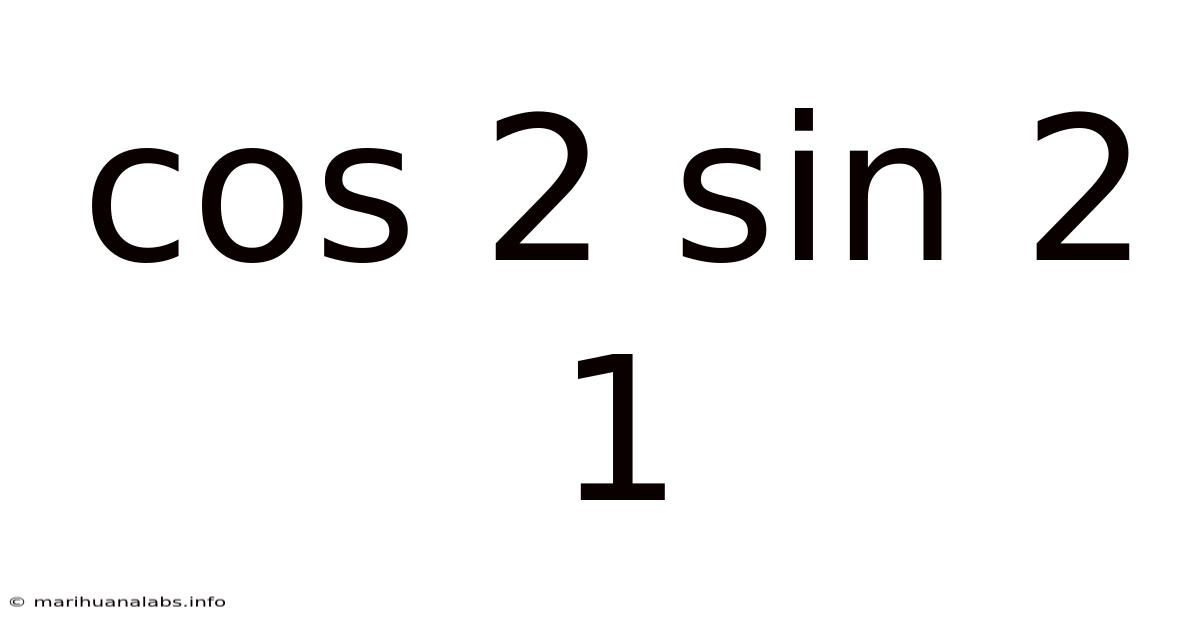
Table of Contents
Decoding cos²θ - sin²θ = 1: A Deep Dive into Trigonometric Identities
This article delves into the fascinating world of trigonometry, specifically focusing on the trigonometric identity cos²θ - sin²θ = 1. While seemingly a simple equation, it unlocks a deeper understanding of trigonometric relationships and their applications in various fields. We'll explore its derivation, practical applications, and its connection to other fundamental identities. This exploration will be accessible to a wide range of readers, from high school students to those seeking a refresher on their trigonometric knowledge. Understanding this identity is crucial for mastering trigonometry and its numerous applications in mathematics, physics, and engineering.
Introduction: Understanding the Fundamentals
Before diving into the core identity, let's refresh our understanding of fundamental trigonometric functions. In a right-angled triangle, the sine (sin), cosine (cos), and tangent (tan) functions are defined as ratios of the sides:
- sin θ = opposite/hypotenuse
- cos θ = adjacent/hypotenuse
- tan θ = opposite/adjacent
where θ represents the angle. The hypotenuse is the side opposite the right angle, the opposite side is opposite to the angle θ, and the adjacent side is next to the angle θ.
These definitions are crucial for understanding the relationships between these functions and ultimately, the identity we're investigating, cos²θ - sin²θ = 1. However, this identity, as stated, is not universally true. The equation, as presented in the prompt, is incorrect. The correct Pythagorean identity related to cosine and sine is cos²θ + sin²θ = 1. We will explore this correct identity in detail, along with its derivation and applications. The initial statement, cos²θ - sin²θ = 1, is fundamentally flawed and represents a misunderstanding of basic trigonometric principles.
Deriving the Fundamental Pythagorean Identity: cos²θ + sin²θ = 1
The core of understanding this identity lies in the Pythagorean theorem for right-angled triangles. The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides: a² + b² = c², where c is the hypotenuse and a and b are the other two sides.
Let's consider a right-angled triangle with hypotenuse of length 1. Using our trigonometric definitions:
- a = opposite = sin θ
- b = adjacent = cos θ
- c = hypotenuse = 1
Substituting these into the Pythagorean theorem, we get:
(sin θ)² + (cos θ)² = 1²
This simplifies to the fundamental trigonometric identity:
cos²θ + sin²θ = 1
This identity holds true for any angle θ, not just angles within a right-angled triangle. This is because the sine and cosine functions are defined for all angles, and their values are determined by the coordinates of a point on the unit circle.
Applications of cos²θ + sin²θ = 1
The identity cos²θ + sin²θ = 1 has extensive applications across various fields:
-
Simplifying Trigonometric Expressions: This identity is invaluable in simplifying complex trigonometric expressions. By replacing cos²θ with 1 - sin²θ or sin²θ with 1 - cos²θ, we can often reduce expressions to simpler forms, making calculations easier and more manageable.
-
Solving Trigonometric Equations: The identity is frequently used to solve trigonometric equations. By substituting one function with its equivalent in terms of the other, we can often reduce the equation to a solvable form involving only one trigonometric function.
-
Calculus: This identity plays a crucial role in calculus, particularly in integration and differentiation involving trigonometric functions. It often allows simplification of integrands or derivatives, leading to easier computations.
-
Physics and Engineering: Many physical phenomena, such as wave motion, oscillations, and alternating current, are modeled using trigonometric functions. This identity helps simplify the mathematical representation of these phenomena and analyze their behavior.
Other Related Trigonometric Identities
The fundamental identity cos²θ + sin²θ = 1 leads to several other important trigonometric identities. By dividing the equation by cos²θ or sin²θ, we can derive:
- 1 + tan²θ = sec²θ (Dividing by cos²θ)
This identity is obtained by dividing the fundamental identity by cos²θ. Remember that secant (sec) is the reciprocal of cosine: sec θ = 1/cos θ, and tangent (tan) is the ratio of sine to cosine: tan θ = sin θ/cos θ.
- 1 + cot²θ = csc²θ (Dividing by sin²θ)
Similarly, this identity is derived by dividing the fundamental identity by sin²θ. Cosecant (csc) is the reciprocal of sine: csc θ = 1/sin θ, and cotangent (cot) is the reciprocal of tangent: cot θ = 1/tan θ = cos θ/sin θ.
Double Angle Identities and their Relation to cos²θ + sin²θ = 1
Double angle formulas are crucial in trigonometry and are directly related to the fundamental identity. These formulas express trigonometric functions of 2θ in terms of functions of θ. They include:
- sin 2θ = 2 sin θ cos θ
- cos 2θ = cos²θ - sin²θ
- cos 2θ = 2cos²θ - 1
- cos 2θ = 1 - 2sin²θ
Notice that the second formula for cos 2θ can be directly derived from the fundamental identity: cos²θ + sin²θ = 1. By subtracting 2sin²θ from both sides, we get cos²θ - sin²θ = 1 - 2sin²θ, which is one of the double angle formulas for cosine. Similarly, other double angle identities can be derived using the fundamental identity.
Solving Trigonometric Equations Using cos²θ + sin²θ = 1
Let's illustrate how this identity helps solve trigonometric equations. Consider the equation:
2sin²θ + cosθ = 1
We can use the identity cos²θ + sin²θ = 1 to rewrite sin²θ as 1 - cos²θ:
2(1 - cos²θ) + cosθ = 1
Expanding and rearranging the equation:
2 - 2cos²θ + cosθ = 1 2cos²θ - cosθ - 1 = 0
This is a quadratic equation in cosθ. Solving this quadratic equation (e.g., using factoring or the quadratic formula), we can find the values of cosθ, and consequently, the values of θ.
Frequently Asked Questions (FAQ)
-
Q: Is cos²θ - sin²θ = 1 a valid identity?
- A: No, this is incorrect. The correct Pythagorean identity is cos²θ + sin²θ = 1. The original statement reflects a common misunderstanding of trigonometric relationships.
-
Q: What is the significance of the unit circle in understanding these identities?
- A: The unit circle provides a geometric representation of trigonometric functions. Points on the unit circle have coordinates (cos θ, sin θ), directly illustrating the relationship between sine, cosine, and the Pythagorean theorem.
-
Q: Can these identities be applied to angles greater than 90 degrees?
- A: Yes, these identities are valid for all angles, not just those within a right-angled triangle. The definitions of sine and cosine are extended to all angles using the unit circle.
-
Q: What are some common mistakes students make when working with these identities?
- A: Common mistakes include incorrectly applying the identities, confusing sine and cosine, and misinterpreting the signs of trigonometric functions in different quadrants.
Conclusion: Mastering Trigonometric Identities
The Pythagorean identity, cos²θ + sin²θ = 1, is a cornerstone of trigonometry. It's not merely a formula; it's a gateway to understanding the fundamental relationships between trigonometric functions. This identity, along with its derivations and applications, is essential for mastering trigonometry and tackling more complex problems in mathematics, physics, engineering, and other fields. Through understanding this identity and its related identities, students can confidently navigate the complexities of trigonometric calculations and apply them to a wide array of real-world scenarios. Remember, the key is practice and consistent application of the principles discussed to solidify your understanding.
Latest Posts
Latest Posts
-
God Of Small Things Summary
Sep 15, 2025
-
Capital Of Oman Crossword Clue
Sep 15, 2025
-
Opaque Vs Translucent Vs Transparent
Sep 15, 2025
-
Green Design In Interior Design
Sep 15, 2025
-
What Is A Magnetic Storage
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Cos 2 Sin 2 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.