9 24 In Simplest Form
marihuanalabs
Sep 08, 2025 · 5 min read
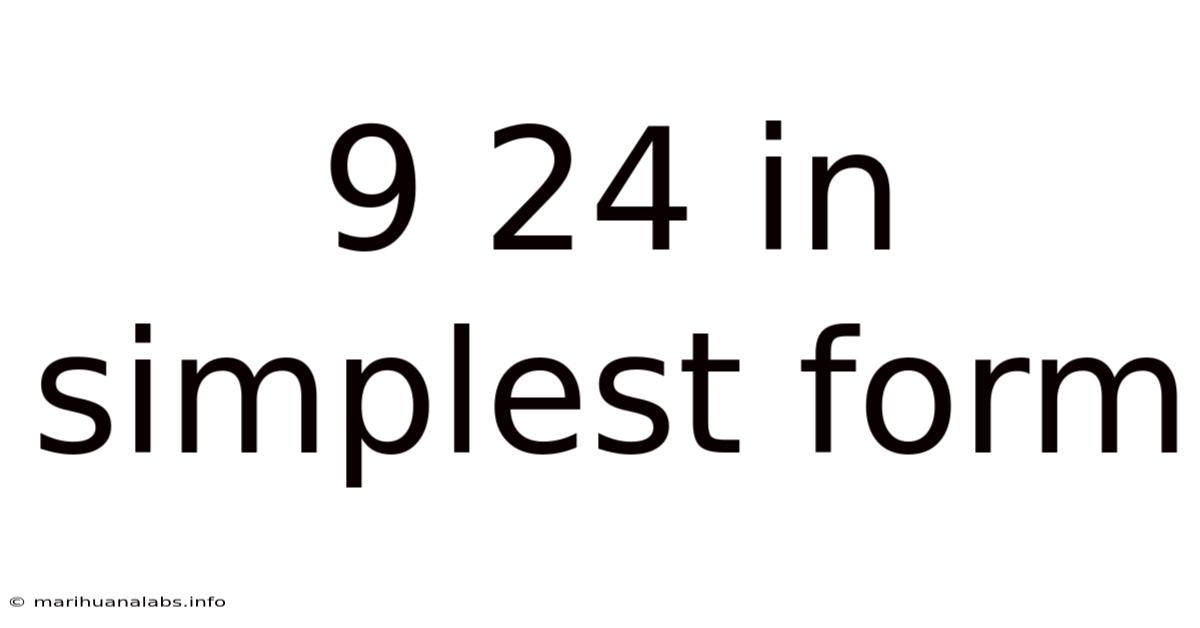
Table of Contents
Simplifying Fractions: A Deep Dive into 9/24
Understanding fractions is a fundamental skill in mathematics, crucial for progressing to more advanced concepts. This article provides a comprehensive guide on simplifying fractions, using the example of 9/24. We'll explore the process step-by-step, delve into the underlying mathematical principles, and address common questions. By the end, you'll not only know the simplest form of 9/24 but also possess a solid understanding of fraction simplification techniques applicable to any fraction.
Understanding Fractions
Before we simplify 9/24, let's establish a basic understanding of fractions. A fraction represents a part of a whole. It's written as a/b, where:
- 'a' is the numerator: This represents the number of parts you have.
- 'b' is the denominator: This represents the total number of equal parts the whole is divided into.
For example, in the fraction 9/24, 9 is the numerator and 24 is the denominator. This means we have 9 parts out of a total of 24 equal parts.
Simplifying Fractions: The Concept of Greatest Common Divisor (GCD)
Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This is achieved by finding the greatest common divisor (GCD), also known as the highest common factor (HCF), of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Finding the GCD is crucial for simplifying fractions efficiently. There are several methods to find the GCD, and we’ll explore a few:
Method 1: Listing Factors
This method involves listing all the factors of both the numerator and the denominator, then identifying the largest common factor.
Factors of 9: 1, 3, 9 Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common factors of 9 and 24 are 1 and 3. The greatest common factor is 3.
Method 2: Prime Factorization
This method involves breaking down the numerator and denominator into their prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11...).
Prime factorization of 9: 3 x 3 = 3² Prime factorization of 24: 2 x 2 x 2 x 3 = 2³ x 3
The common prime factor is 3. Therefore, the GCD is 3.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a more efficient method for finding the GCD of larger numbers. It's based on the principle that the GCD of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCD.
Let's apply the Euclidean algorithm to 9 and 24:
- 24 ÷ 9 = 2 with a remainder of 6
- 9 ÷ 6 = 1 with a remainder of 3
- 6 ÷ 3 = 2 with a remainder of 0
The last non-zero remainder is 3, so the GCD of 9 and 24 is 3.
Simplifying 9/24
Now that we've determined the GCD of 9 and 24 is 3, we can simplify the fraction:
Divide both the numerator and the denominator by the GCD (3):
9 ÷ 3 = 3 24 ÷ 3 = 8
Therefore, the simplest form of 9/24 is 3/8.
Visual Representation
Imagine a pizza cut into 24 equal slices. 9/24 represents having 9 of those slices. If we group the slices into sets of 3, we have 3 groups of 3 slices out of a total of 8 groups of 3 slices. This visually demonstrates how 9/24 simplifies to 3/8.
Further Exploration: Understanding Equivalent Fractions
Simplifying a fraction doesn't change its value; it just expresses it in a more concise form. 9/24 and 3/8 are equivalent fractions. They represent the same portion of a whole. You can create equivalent fractions by multiplying or dividing both the numerator and denominator by the same non-zero number.
Practical Applications of Fraction Simplification
Simplifying fractions is essential in various fields, including:
- Cooking and Baking: Following recipes often involves working with fractions. Simplifying fractions makes it easier to understand and measure ingredients accurately.
- Construction and Engineering: Precise measurements are critical in construction and engineering. Simplifying fractions ensures accuracy and efficiency in calculations.
- Finance: Working with percentages and proportions often involves fraction simplification for clearer understanding and analysis.
- Data Analysis: Simplifying fractions helps in representing data concisely and interpreting results more easily.
Frequently Asked Questions (FAQ)
Q1: What if the numerator and denominator have no common factors other than 1?
A1: If the GCD is 1, the fraction is already in its simplest form. For example, 7/11 is already in its simplest form.
Q2: Can I simplify a fraction by just dividing the numerator and denominator by any number?
A2: No, you must divide both the numerator and denominator by their GCD to obtain the simplest form. Dividing by any other number will result in an equivalent fraction, but not necessarily the simplest form.
Q3: Is there a shortcut to simplifying fractions quickly?
A3: While prime factorization is generally reliable, with practice, you can often spot common factors quickly. For example, if both numerator and denominator are even, you know you can at least divide by 2. Similarly, if both end in 0 or 5, you can divide by 5.
Q4: What happens if the numerator is larger than the denominator?
A4: If the numerator is larger than the denominator, you have an improper fraction. You can simplify it the same way as a proper fraction (numerator smaller than denominator) and then convert it to a mixed number (whole number and a fraction). For example, 27/9 simplifies to 3/1, which is simply 3.
Conclusion
Simplifying fractions is a vital skill in mathematics. By understanding the concept of the greatest common divisor and applying different methods to find it, you can efficiently reduce any fraction to its simplest form. This process not only makes fractions easier to understand and work with but also provides a foundation for more advanced mathematical concepts. Remember that the simplest form of 9/24 is 3/8, and the methods outlined here provide a solid framework for tackling any fraction simplification challenge you encounter. Practice makes perfect – so keep practicing and you'll become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
Pyramid Of Numbers Food Chain
Sep 09, 2025
-
How Smart Are U Test
Sep 09, 2025
-
What Is You In French
Sep 09, 2025
-
Capacitors In Parallel Vs Series
Sep 09, 2025
-
150ml Of Milk In Cups
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 9 24 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.