9 20 As A Decimal
marihuanalabs
Sep 12, 2025 · 5 min read
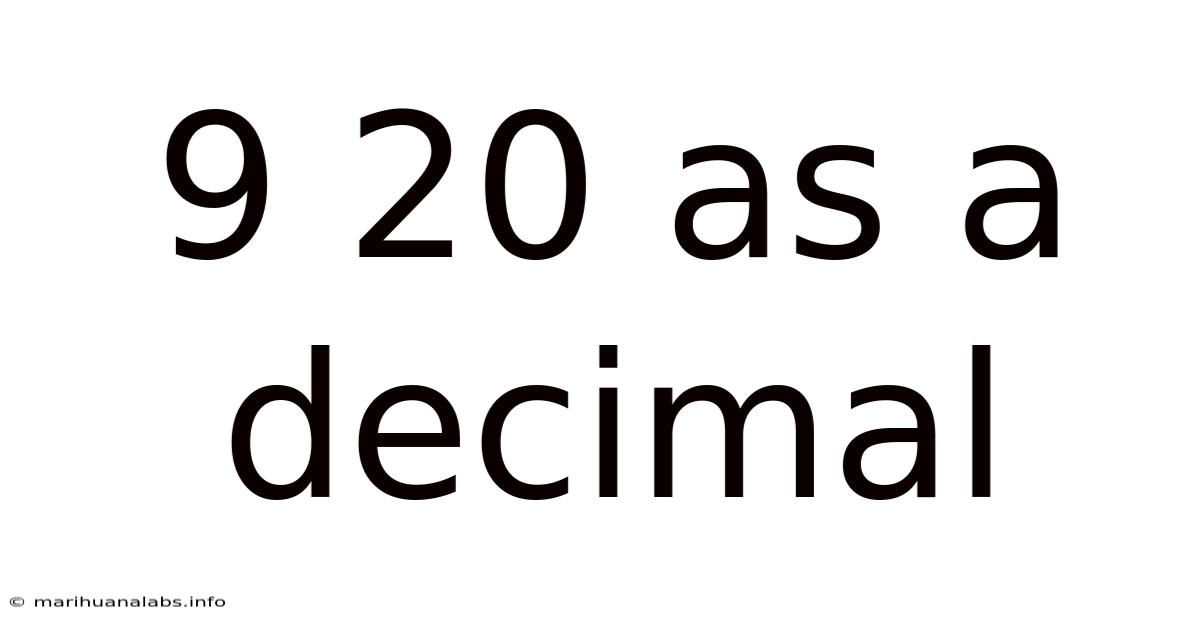
Table of Contents
Decoding 9/20 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific studies. This comprehensive guide will delve deep into the conversion of the fraction 9/20 into its decimal equivalent, exploring different methods, underlying principles, and practical applications. We'll also address common questions and misconceptions surrounding this seemingly simple conversion. By the end, you'll not only know the answer but also understand the why behind the process.
Introduction: Understanding Fractions and Decimals
Before we dive into the conversion of 9/20, let's briefly review the basics of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). A decimal, on the other hand, represents a part of a whole using the base-10 system, with a decimal point separating the whole number part from the fractional part.
The fraction 9/20 signifies 9 parts out of a total of 20 equal parts. Our goal is to express this same proportion using the decimal system.
Method 1: Direct Division
The most straightforward method for converting a fraction to a decimal is through direct division. We simply divide the numerator (9) by the denominator (20).
9 ÷ 20 = 0.45
Therefore, 9/20 as a decimal is 0.45.
This method is simple and easily performed using a calculator or even long division by hand. Let's explore the long division process for a deeper understanding:
0.45
20 | 9.00
8.0
----
1.00
1.00
----
0
As you can see, dividing 9 by 20 results in a quotient of 0.45 with no remainder.
Method 2: Equivalent Fractions and Decimal Representation
Another approach involves converting the fraction into an equivalent fraction with a denominator that is a power of 10 (e.g., 10, 100, 1000, etc.). This allows for a direct conversion to a decimal.
To achieve this with 9/20, we need to find a number that, when multiplied by 20, results in a power of 10. In this case, multiplying the denominator by 5 gives us 100:
(9/20) * (5/5) = 45/100
Since 100 is 10², we can easily express 45/100 as a decimal:
45/100 = 0.45
This method highlights the relationship between fractions and decimals, illustrating how different representations can express the same value.
Method 3: Understanding Place Value
Decimal numbers represent values based on their position relative to the decimal point. Each position to the right of the decimal point represents a decreasing power of 10: tenths (1/10), hundredths (1/100), thousandths (1/1000), and so on.
In the case of 0.45, the '4' represents 4 tenths (4/10) and the '5' represents 5 hundredths (5/100). Adding these together gives us:
(4/10) + (5/100) = (40/100) + (5/100) = 45/100 = 0.45
This approach reinforces the understanding of the decimal system and how it relates to fractions.
Practical Applications of Decimal Conversion
The ability to convert fractions to decimals has numerous practical applications across various fields:
-
Finance: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals. For instance, a 9/20 discount translates to a 0.45 or 45% discount.
-
Engineering and Science: Many engineering and scientific calculations require precise measurements and calculations, making the conversion of fractions to decimals essential for accuracy.
-
Data Analysis: In data analysis and statistics, working with decimal representations is often more convenient than fractions, especially when using computer software or statistical tools.
-
Everyday Life: Even in everyday life, situations may arise where converting fractions to decimals simplifies calculations, such as dividing a pizza or sharing a bill equally.
Further Exploration: Converting More Complex Fractions
While 9/20 is a relatively straightforward fraction to convert, the principles discussed here can be applied to more complex fractions. For fractions with denominators that are not easily converted to powers of 10, direct division remains the most reliable method. However, understanding equivalent fractions can often simplify the process.
For example, consider the fraction 7/16. While not easily converted to a power of 10, you can perform long division to find its decimal equivalent (0.4375).
Addressing Common Misconceptions
A common misconception is that all fractions convert to terminating decimals (decimals that end). This is not true. Fractions with denominators that contain prime factors other than 2 and 5 will result in repeating decimals (decimals with a repeating pattern of digits). For instance, 1/3 converts to 0.333... (a repeating decimal).
Frequently Asked Questions (FAQ)
-
Q: Is 0.45 the only decimal representation of 9/20?
- A: Yes, 0.45 is the only decimal representation of 9/20. It's a terminating decimal, meaning it has a finite number of digits.
-
Q: How can I convert a repeating decimal back to a fraction?
- A: Converting a repeating decimal back to a fraction involves algebraic manipulation. It's a more advanced topic but involves setting up an equation and solving for the fraction.
-
Q: Are there any online tools to help with fraction-to-decimal conversion?
- A: Yes, many online calculators and converters are available to assist with this conversion.
-
Q: What is the significance of the decimal point?
- A: The decimal point separates the whole number part from the fractional part of a number. It signifies the ones place, and everything to the right represents parts of one.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting fractions to decimals, as demonstrated with the example of 9/20, is a fundamental skill with broad applications. Mastering this skill involves understanding the underlying principles of fractions, decimals, and the different methods available for conversion. Whether you choose direct division, equivalent fractions, or a place value approach, a clear understanding of these concepts will empower you to tackle more complex conversions with confidence. Remember, practice is key – the more you practice, the more comfortable and proficient you will become in converting fractions to decimals and vice-versa. This understanding forms a solid foundation for further mathematical exploration and problem-solving.
Latest Posts
Latest Posts
-
Is An Equilateral Triangle Isosceles
Sep 13, 2025
-
Theseus And The Minotaur Summary
Sep 13, 2025
-
Two Gentlemen Of Verona Summary
Sep 13, 2025
-
Spanish For I Am Good
Sep 13, 2025
-
The Duchess Of Malfi London
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 9 20 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.