9 12 As A Percentage
marihuanalabs
Sep 21, 2025 · 5 min read
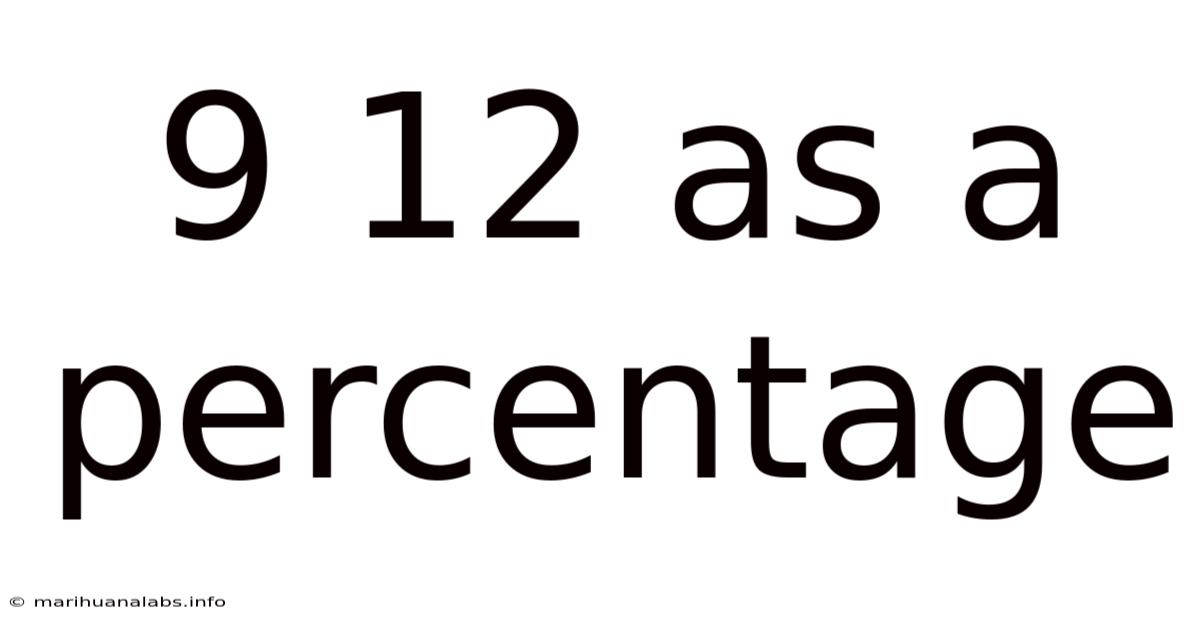
Table of Contents
Understanding 9/12 as a Percentage: A Comprehensive Guide
Many situations in daily life require us to convert fractions into percentages. Whether it's calculating grades, understanding discounts, or analyzing financial data, the ability to express fractions as percentages is crucial. This article will comprehensively guide you through understanding how to convert the fraction 9/12 into a percentage, and explore related concepts to deepen your understanding of percentages and fractions. We'll cover the step-by-step process, the underlying mathematical principles, and answer frequently asked questions. By the end, you'll not only know the answer but also possess a solid foundation for tackling similar percentage calculations.
Understanding Fractions and Percentages
Before diving into the calculation, let's review the fundamentals. A fraction represents a part of a whole. In the fraction 9/12, 9 is the numerator (the part) and 12 is the denominator (the whole). A percentage, on the other hand, represents a fraction out of 100. The symbol "%" signifies "per hundred." Therefore, converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100.
Method 1: Simplifying the Fraction and then Converting to Percentage
The most straightforward method involves simplifying the fraction first, and then converting the simplified fraction to a percentage.
Step 1: Simplify the Fraction
The fraction 9/12 can be simplified by finding the greatest common divisor (GCD) of 9 and 12, which is 3. Dividing both the numerator and the denominator by 3, we get:
9 ÷ 3 = 3 12 ÷ 3 = 4
Therefore, 9/12 simplifies to 3/4.
Step 2: Convert the Simplified Fraction to a Decimal
To convert the fraction 3/4 to a decimal, we divide the numerator (3) by the denominator (4):
3 ÷ 4 = 0.75
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol:
0.75 × 100 = 75%
Therefore, 9/12 is equal to 75%.
Method 2: Direct Conversion to Percentage
This method involves directly converting the fraction to a percentage without simplifying first.
Step 1: Convert the Fraction to a Decimal
Divide the numerator (9) by the denominator (12):
9 ÷ 12 = 0.75
Step 2: Convert the Decimal to a Percentage
Multiply the decimal by 100 and add the "%" symbol:
0.75 × 100 = 75%
This method yields the same result: 9/12 is equal to 75%.
The Mathematical Principle Behind the Conversion
The conversion from a fraction to a percentage relies on the fundamental concept of proportionality. We are essentially finding an equivalent fraction where the denominator is 100. The process can be represented mathematically as follows:
(Numerator / Denominator) × 100% = Percentage
In our case:
(9 / 12) × 100% = 75%
This equation demonstrates that we are scaling the fraction to a base of 100, which is the essence of percentage calculation.
Real-World Applications of Percentage Calculations
Understanding how to convert fractions to percentages has numerous practical applications:
- Academic Performance: Calculating grades often involves converting the number of correct answers to a percentage of the total questions.
- Financial Calculations: Interest rates, discounts, taxes, and profit margins are all expressed as percentages.
- Data Analysis: Representing data as percentages allows for easier comparison and interpretation. For instance, analyzing market share or survey results.
- Everyday Life: Understanding sales discounts (e.g., a 25% off sale), calculating tips in restaurants, or determining the percentage of ingredients in a recipe all involve percentage calculations.
Further Exploring Fractions and Percentages: Equivalent Fractions
It's crucial to understand that many fractions can represent the same percentage. For example, 3/4, 6/8, 9/12, and 12/16 are all equivalent fractions, and they all represent 75%. This concept is essential for simplifying fractions and understanding different representations of the same proportion. The ability to find equivalent fractions is crucial for simplifying calculations and making comparisons.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying the fraction helpful?
A1: Simplifying the fraction makes the subsequent decimal and percentage conversion easier. Working with smaller numbers reduces the risk of calculation errors.
Q2: Can I convert any fraction to a percentage?
A2: Yes, you can convert any fraction to a percentage using the methods described above. The result might be a whole number percentage (e.g., 75%) or a percentage with a decimal component (e.g., 66.67%).
Q3: What if the decimal resulting from the fraction division is non-terminating (e.g., 1/3)?
A3: Non-terminating decimals often result in percentages with repeating decimal parts. In these cases, you can round the percentage to a suitable number of decimal places for practical purposes. For example, 1/3 = 0.3333... which is approximately 33.33%.
Q4: What are some common percentage equivalents of simple fractions?
A4: It's useful to memorize some common equivalents:
- 1/2 = 50%
- 1/4 = 25%
- 3/4 = 75%
- 1/3 ≈ 33.33%
- 2/3 ≈ 66.67%
- 1/5 = 20%
- 1/10 = 10%
Conclusion: Mastering Percentage Calculations
Converting fractions to percentages is a fundamental skill with wide-ranging applications. By understanding the underlying mathematical principles and applying the step-by-step methods described in this article, you can confidently convert any fraction to its equivalent percentage. Remember to practice regularly to solidify your understanding and build your proficiency. Mastering this skill will significantly enhance your ability to analyze data, solve problems, and navigate various aspects of daily life and professional endeavors. The seemingly simple task of converting 9/12 to 75% opens the door to a broader understanding of mathematical concepts and their practical applications.
Latest Posts
Latest Posts
-
Images Of Christmas With Jesus
Sep 21, 2025
-
Where Are You In French
Sep 21, 2025
-
Group Of Bats Is Called
Sep 21, 2025
-
125 Degrees F To C
Sep 21, 2025
-
Psychology A Level Research Methods
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 9 12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.