8 7 As A Percent
marihuanalabs
Sep 17, 2025 · 5 min read
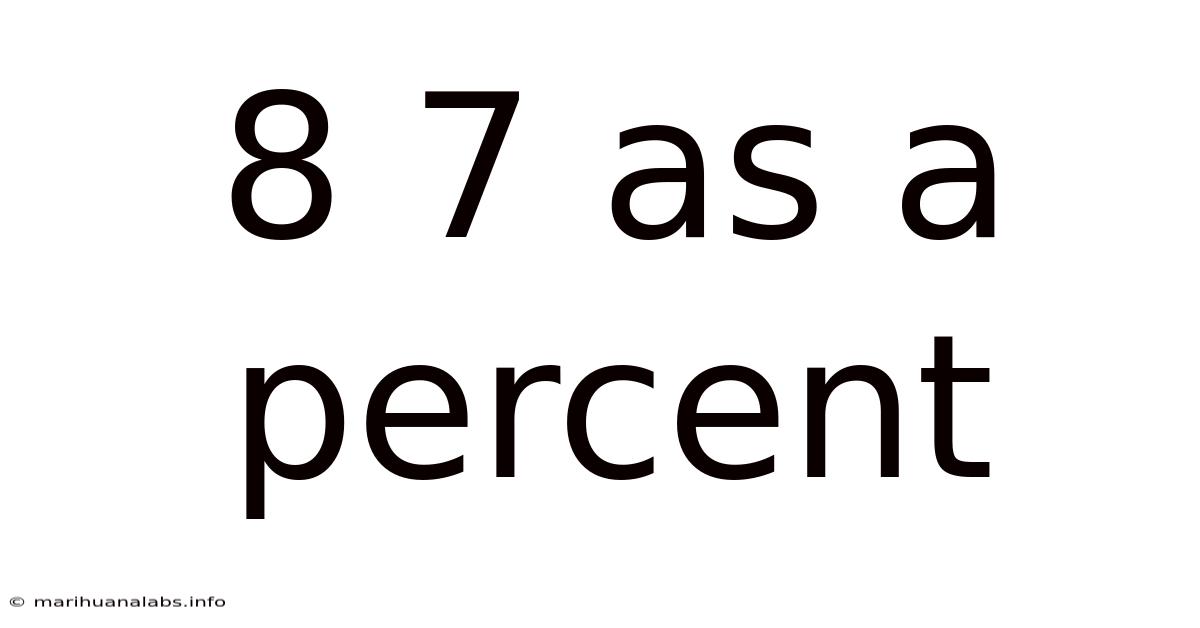
Table of Contents
Decoding 8/7 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications across numerous fields, from finance and statistics to everyday calculations. This article delves deep into the conversion of the fraction 8/7 into a percentage, explaining the process step-by-step and exploring the underlying mathematical principles. We'll also address common questions and misconceptions surrounding percentage calculations. By the end, you'll not only know the answer but also understand why the answer is what it is.
Understanding Fractions and Percentages
Before we dive into the specifics of converting 8/7, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In the fraction 8/7, 8 is the numerator and 7 is the denominator. This means we have 8 parts out of a total of 7 parts. Notice that this is an improper fraction, where the numerator is larger than the denominator. This indicates a value greater than one whole.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion relative to 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. The core idea is to express a fraction in terms of a common denominator of 100.
Converting 8/7 to a Percentage: A Step-by-Step Approach
Converting 8/7 to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal.
To do this, we simply divide the numerator (8) by the denominator (7):
8 ÷ 7 ≈ 1.142857
The result is an approximate decimal value because the division results in a recurring decimal (1.142857142857...). We'll use a rounded value for further calculations, keeping in mind this inherent imprecision. The more decimal places you use, the more accurate your final percentage will be.
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%):
1.142857 × 100 ≈ 114.29%
Therefore, 8/7 is approximately equal to 114.29%.
Understanding the Result: More Than 100%
The result, 114.29%, might seem unusual at first. Percentages are often thought of as being between 0% and 100%. However, this is only true when dealing with fractions where the numerator is less than or equal to the denominator (proper fractions). Since 8/7 is an improper fraction, it represents a quantity greater than one whole. This explains why the percentage is greater than 100%. It signifies that 8/7 is 114.29% of the whole, meaning it exceeds the whole by 14.29%.
Think of it like this: if you have a pizza cut into 7 slices, and you eat 8 slices, you've eaten more than one whole pizza.
Illustrative Examples in Real-World Scenarios
Let's consider a few scenarios to better grasp the concept of percentages exceeding 100%:
-
Investment Returns: If you invest $100 and your investment grows to $114.29, your return is 14.29%. But if your investment grows to $180, you would calculate the percentage increase as 80/100 x 100 = 80%, or a 80% increase. If your investment grew to $170, that represents a 70% increase. However, if your investment increased to $180, this signifies a 80% increase and is clearly more than 100%. Representing this as a fraction would be 180/100 which simplifies to 9/5. If the investment grew by even more, resulting in a value of, for example, $200, then the return on investment would be 200/100 = 200%, which represents more than double the original investment.
-
Production Increase: A factory producing 100 units per day might increase its production to 114.29 units the following day. This represents a 14.29% increase.
-
Population Growth: If a town's population grows from 700 to 800, the increase is 100/700, which is approximately 14.29%. If the population were to increase to 1000, the percentage increase would be 300/700 (approximately 42.86%). Note that in these cases, a percentage increase is always calculated as a proportion of the original value.
Advanced Concepts and Further Exploration
While converting 8/7 to a percentage is relatively straightforward, the underlying mathematical principles extend to more complex scenarios:
-
Recurring Decimals: The conversion of 8/7 involved a recurring decimal. Understanding how to handle recurring decimals is crucial for accurate percentage calculations. Often, rounding to a suitable number of decimal places is necessary for practical applications.
-
Percentage Change: Calculating percentage increase or decrease involves comparing two values. This is a common application in fields like finance and economics.
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Understanding percentage calculations is fundamental to grasping the concept of compound interest.
-
Statistical Analysis: Percentages are frequently used to represent proportions and probabilities in statistical analysis.
Frequently Asked Questions (FAQ)
Q: Why is 8/7 greater than 1?
A: Because the numerator (8) is larger than the denominator (7). This signifies that the fraction represents more than one whole unit.
Q: Can a percentage be more than 100%?
A: Yes, absolutely. This occurs when dealing with improper fractions (numerator > denominator), representing a quantity greater than one whole.
Q: How accurate is the 114.29% result?
A: It's an approximation. The decimal representation of 8/7 is a recurring decimal, so any percentage value will be an approximation based on the number of decimal places used in the calculation.
Q: What if I want a more precise percentage?
A: Use more decimal places in your decimal to percentage conversion. The more decimal places you include, the more precise your final percentage will be. However, for most practical purposes, 114.29% provides sufficient accuracy.
Conclusion
Converting 8/7 to a percentage provides a practical example of how to handle improper fractions and understand percentages exceeding 100%. The process involves converting the fraction to a decimal and then multiplying by 100 to obtain the percentage. Remember that percentages are a powerful tool for expressing proportions and comparing quantities, and understanding their application extends far beyond basic arithmetic. Mastering this fundamental skill opens the door to a more profound understanding of mathematical concepts in various fields. The ability to confidently convert fractions to percentages is a valuable asset in various academic, professional, and everyday situations.
Latest Posts
Latest Posts
-
All The Best In Spanish
Sep 17, 2025
-
How Many Qurans Are There
Sep 17, 2025
-
Molecular Orbital Configuration Of Co
Sep 17, 2025
-
Semi Finished Weighted Average Index
Sep 17, 2025
-
Hcf Of 98 And 42
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 8 7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.