8 25 As A Percentage
marihuanalabs
Sep 20, 2025 · 4 min read
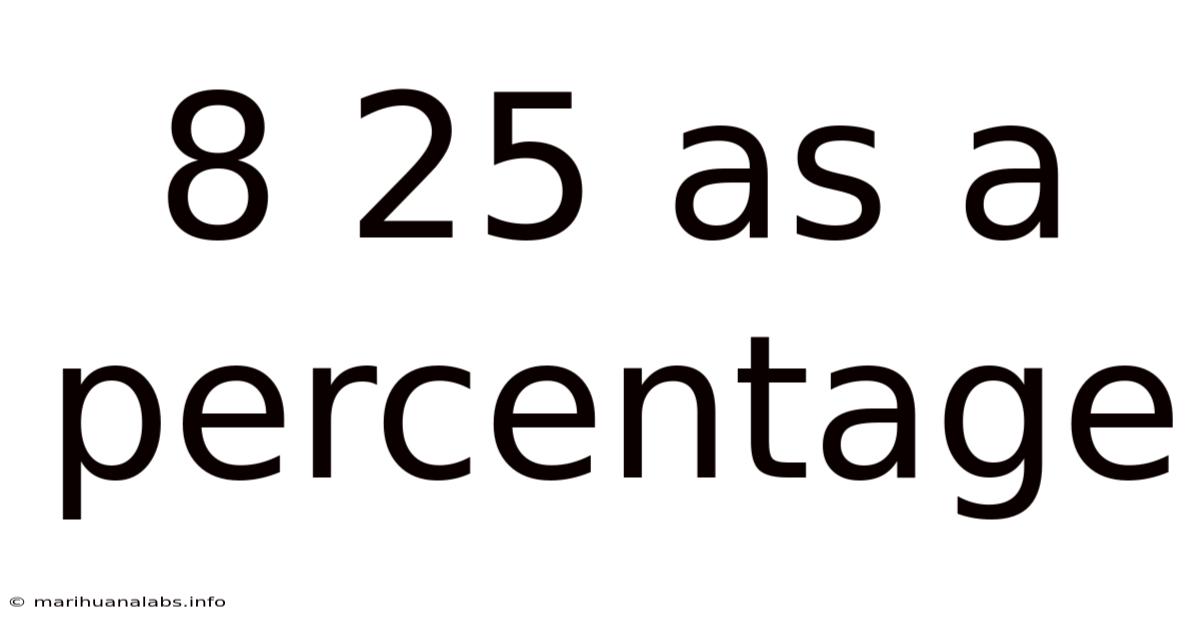
Table of Contents
8/25 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This comprehensive guide will delve into the conversion of the fraction 8/25 into a percentage, exploring different methods, providing detailed explanations, and addressing common questions. We'll also examine the broader context of fraction-to-percentage conversion and its practical relevance.
Understanding Fractions and Percentages
Before diving into the conversion of 8/25, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates the total number of parts the whole is divided into.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion out of a hundred. For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
Method 1: Converting the Fraction to a Decimal
The most straightforward method to convert 8/25 to a percentage involves first converting the fraction into a decimal. This is done by dividing the numerator (8) by the denominator (25):
8 ÷ 25 = 0.32
Now, to express this decimal as a percentage, we simply multiply by 100:
0.32 x 100 = 32%
Therefore, 8/25 is equal to 32%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves finding an equivalent fraction of 8/25 that has a denominator of 100. This is because percentages are based on a denominator of 100. To achieve this, we need to determine what number we must multiply the denominator (25) by to get 100.
25 x 4 = 100
Since we multiplied the denominator by 4, we must also multiply the numerator by 4 to maintain the fraction's value:
8 x 4 = 32
This gives us the equivalent fraction 32/100, which directly translates to 32%.
Method 3: Using Proportions
We can also solve this using proportions. We can set up a proportion where x represents the percentage we're trying to find:
8/25 = x/100
To solve for x, we cross-multiply:
25x = 800
Now, divide both sides by 25:
x = 800 ÷ 25 = 32
Therefore, x = 32, meaning 8/25 is equal to 32%.
Understanding the Result: 32%
The result, 32%, signifies that 8 out of 25 represents 32 parts out of 100. This percentage can be used to represent various scenarios. For example, if you answered 8 out of 25 questions correctly on a test, your score would be 32%. Or, if 8 out of 25 apples in a basket are red, then 32% of the apples are red.
Practical Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages has numerous practical applications:
- Calculating Grades and Scores: As mentioned above, this is crucial for determining academic performance.
- Financial Calculations: Percentage calculations are fundamental in finance, such as calculating interest rates, discounts, profits, and losses.
- Data Analysis and Statistics: Representing data as percentages allows for easier comparison and interpretation of proportions.
- Everyday Life: From calculating tips in restaurants to understanding sales discounts, percentage calculations are frequently used in daily life.
Beyond 8/25: Generalizing the Fraction-to-Percentage Conversion
The methods described above can be applied to any fraction. The general formula is:
(Numerator / Denominator) x 100 = Percentage
This formula provides a universal approach to converting any fraction into its percentage equivalent.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to convert 8/25 to a percentage?
A: Yes, absolutely. Simply divide 8 by 25 and then multiply the result by 100. Most calculators have a percentage function that can simplify this process.
-
Q: What if the fraction results in a decimal with many digits after the decimal point?
A: In such cases, you can round the decimal to a certain number of decimal places depending on the required level of precision. For example, if the decimal is 0.32456, you might round it to 0.32 or 0.325.
-
Q: Are there any other methods to convert fractions to percentages?
A: While the methods discussed are the most common and straightforward, you can also use ratio and proportion methods or utilize online converters for quick calculations.
-
Q: Why is understanding percentage conversion important?
A: Understanding percentage conversion is critical for interpreting data, making informed decisions, and applying mathematical concepts in various real-world situations.
Conclusion
Converting 8/25 to a percentage, which equals 32%, is a straightforward process achievable through several methods. Understanding these methods provides a strong foundation for working with fractions and percentages, which are essential mathematical concepts applicable in a wide range of contexts. The ability to confidently convert fractions to percentages empowers individuals to better interpret data, solve problems, and make informed decisions in various aspects of their lives, from academic pursuits to financial planning and beyond. Mastering this skill is a valuable asset in navigating the numerical world. Remember that the key is to understand the underlying principles, and the specific method chosen is largely a matter of personal preference and the tools available.
Latest Posts
Latest Posts
-
Potential Drop Across A Resistor
Sep 20, 2025
-
Net Worth Of Gregory Peck
Sep 20, 2025
-
87 Degrees F To C
Sep 20, 2025
-
Group Of Goats Are Called
Sep 20, 2025
-
The Ice Palace Tarjei Vesaas
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 8 25 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.