8 12 As A Percentage
marihuanalabs
Sep 11, 2025 · 5 min read
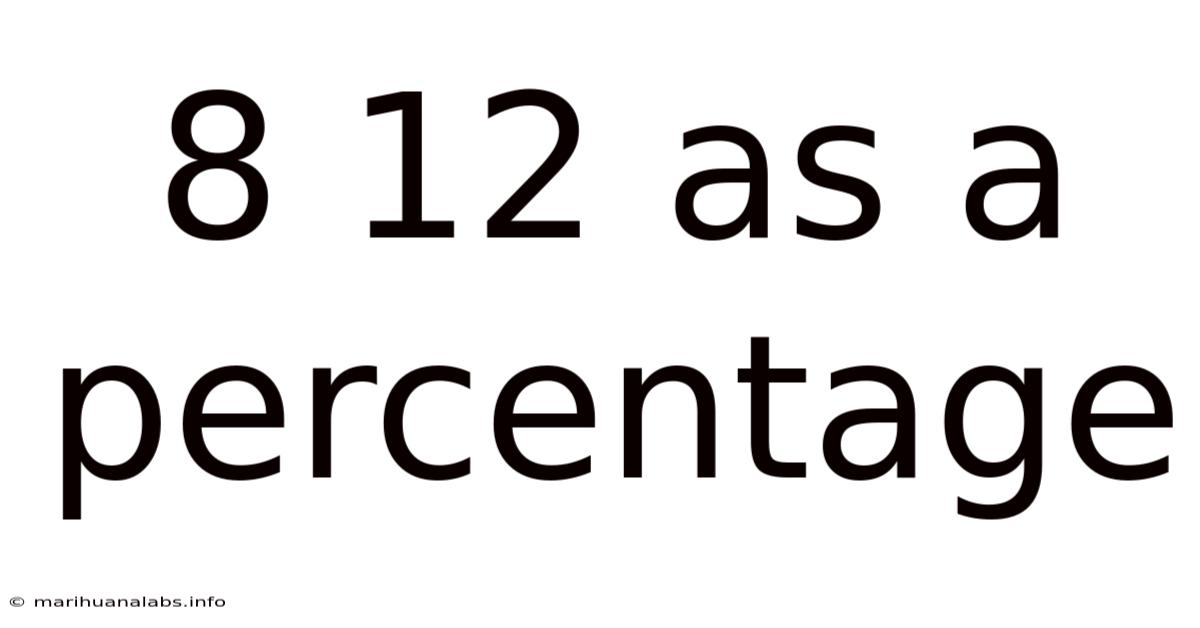
Table of Contents
Decoding the Percentage: Understanding 8/12 as a Percentage
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts to understanding financial reports. This article delves deep into converting the fraction 8/12 into a percentage, exploring the underlying concepts, different calculation methods, and real-world examples. We’ll also address common misconceptions and answer frequently asked questions to provide a comprehensive understanding of this seemingly simple, yet important, mathematical concept.
Understanding Fractions and Percentages
Before we tackle the specific calculation of 8/12 as a percentage, let's establish a firm understanding of the core concepts involved. A fraction represents a part of a whole. In the fraction 8/12, 8 is the numerator (the part) and 12 is the denominator (the whole). A percentage, on the other hand, is a way of expressing a number as a fraction of 100. The percentage symbol (%) signifies "out of 100". Therefore, converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100.
Method 1: Direct Conversion using Division
The most straightforward method for converting 8/12 to a percentage involves dividing the numerator by the denominator and then multiplying the result by 100.
-
Divide the numerator by the denominator: 8 ÷ 12 = 0.666666... (this is a recurring decimal)
-
Multiply the result by 100: 0.666666... × 100 = 66.6666...%
Therefore, 8/12 is approximately equal to 66.67%. The recurring decimal means that the percentage is not perfectly precise; we round it to two decimal places for practical purposes.
Method 2: Simplifying the Fraction First
Simplifying the fraction before conversion can make the calculation easier and reduce the chance of rounding errors. Both 8 and 12 are divisible by 4.
-
Simplify the fraction: 8/12 simplifies to 2/3 by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 4.
-
Convert the simplified fraction to a decimal: 2 ÷ 3 = 0.666666...
-
Multiply the decimal by 100: 0.666666... × 100 = 66.6666...%
Again, we arrive at approximately 66.67%. This method highlights the importance of simplifying fractions; it streamlines the calculation and improves accuracy.
Method 3: Using Proportions
This method uses the concept of proportions to find the equivalent percentage. We set up a proportion:
8/12 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
12x = 800
x = 800 ÷ 12
x = 66.6666...
Therefore, 8/12 is approximately 66.67%. This method clearly demonstrates the relationship between the fraction and its percentage equivalent.
The Significance of Understanding 8/12 as a Percentage
The ability to accurately convert fractions to percentages is crucial in various real-world applications:
-
Financial Calculations: Calculating interest rates, discounts, profit margins, and tax rates all involve working with percentages. Understanding 8/12 as 66.67% could be useful in assessing the performance of investments or understanding loan terms.
-
Data Analysis: Representing data in percentages often makes it easier to understand and compare. For example, if 8 out of 12 students passed an exam, representing this as 66.67% provides a clearer picture of the overall performance.
-
Everyday Life: Calculating tips in restaurants, figuring out sales discounts, or understanding survey results all rely on converting fractions to percentages. A grasp of percentages empowers individuals to make informed decisions in numerous everyday situations.
-
Scientific Applications: In science and engineering, representing data as percentages is a common practice for comparing experimental results or expressing probability.
Addressing Common Misconceptions
A common mistake is to simply multiply the numerator by 100. This approach ignores the denominator and yields an incorrect result. It's crucial to remember that the percentage represents the proportion of the numerator to the denominator, not the numerator's absolute value.
Another common error is incorrectly rounding the percentage. While 66.67% is a practical approximation, understanding the recurring nature of the decimal (66.666...) is important for precise calculations. The level of rounding precision depends on the context; for most everyday situations, two decimal places suffice.
Frequently Asked Questions (FAQ)
-
Q: Can 8/12 be expressed as a simpler fraction?
-
A: Yes, 8/12 can be simplified to 2/3 by dividing both the numerator and denominator by their greatest common divisor, which is 4.
-
Q: Is 66.67% the exact percentage equivalent of 8/12?
-
A: No, 66.67% is an approximation. The exact equivalent is a recurring decimal: 66.666...%
-
Q: How can I convert other fractions to percentages?
-
A: Follow the same steps outlined above: divide the numerator by the denominator and multiply the result by 100. Simplify the fraction beforehand if possible to ease the calculation.
-
Q: Why is understanding percentages important?
-
A: Percentages provide a standardized and easily understandable way to represent proportions and compare different quantities, making them invaluable in various fields.
Conclusion
Converting 8/12 to a percentage highlights the importance of understanding fundamental mathematical concepts. While the answer, approximately 66.67%, might seem simple, the underlying principles – fractions, decimals, percentages, and simplification – are essential for various mathematical and real-world applications. This detailed explanation, encompassing different methods and addressing common misconceptions, aims to equip you with the knowledge and confidence to tackle similar percentage calculations with ease and accuracy. Mastering this skill enhances problem-solving capabilities and fosters a stronger understanding of mathematical relationships. Remember to practice different methods and apply your knowledge in various contexts to solidify your understanding.
Latest Posts
Latest Posts
-
Lesser Than Macbeth And Greater
Sep 11, 2025
-
I Speak Spanish In English
Sep 11, 2025
-
Stars In Ursa Major Constellation
Sep 11, 2025
-
National Game Of Sri Lanka
Sep 11, 2025
-
How Far Is Dublin Ireland
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 8 12 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.