75/100 In Its Simplest Form
marihuanalabs
Sep 09, 2025 · 6 min read
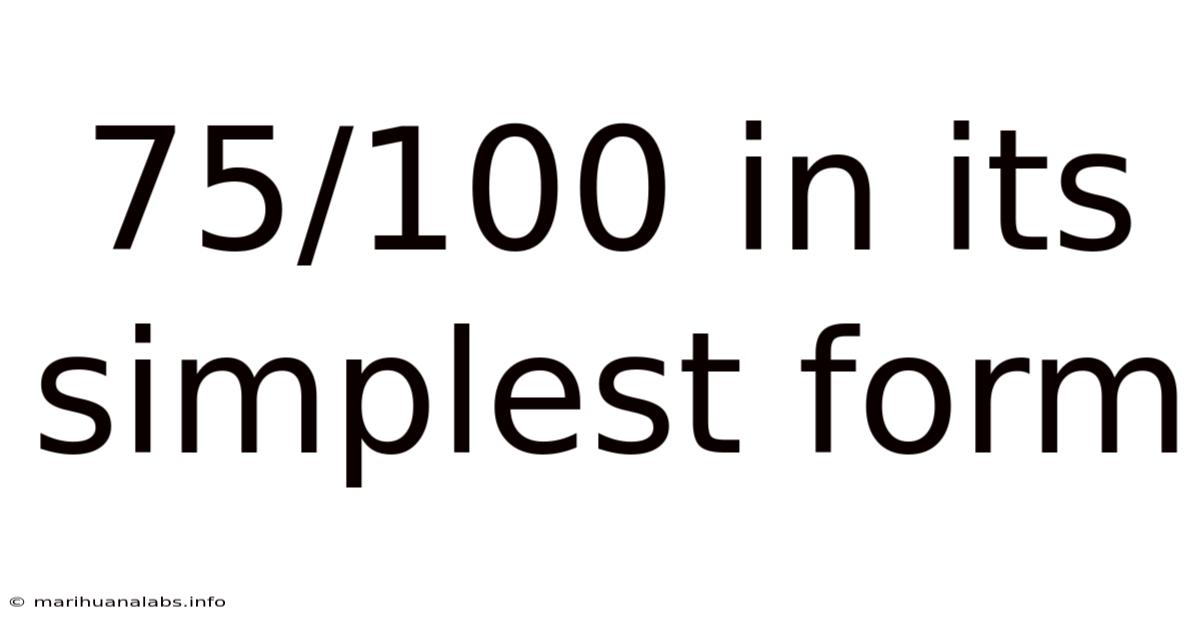
Table of Contents
75/100 in its Simplest Form: A Comprehensive Guide to Fraction Simplification
Understanding fractions is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific concepts. Often, we encounter fractions that aren't presented in their simplest, most efficient form. This article will comprehensively explore how to simplify fractions, using the example of 75/100 to illustrate the process and delve into the underlying mathematical principles. We'll cover various methods, address common misconceptions, and answer frequently asked questions, making fraction simplification easy to understand for everyone, regardless of their mathematical background.
Introduction: What Does "Simplest Form" Mean?
When we talk about a fraction being in its simplest form, or lowest terms, we mean that the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. In essence, we've divided both the top and bottom by their greatest common divisor (GCD). This makes the fraction easier to understand and work with in calculations. For example, 75/100 isn't in its simplest form because both 75 and 100 share common factors greater than 1. Our goal is to find the equivalent fraction that represents the same value but uses the smallest possible whole numbers.
Method 1: Finding the Greatest Common Divisor (GCD)
The most reliable way to simplify a fraction is by finding the GCD of the numerator and the denominator. The GCD is the largest number that divides both numbers without leaving a remainder. There are several ways to find the GCD:
-
Listing Factors: Write down all the factors of both numbers. The largest number that appears in both lists is the GCD. For 75 and 100:
Factors of 75: 1, 3, 5, 15, 25, 75 Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100
The largest common factor is 25.
-
Prime Factorization: Break down each number into its prime factors (numbers divisible only by 1 and themselves). The GCD is the product of the common prime factors raised to the lowest power.
75 = 3 x 5 x 5 = 3 x 5² 100 = 2 x 2 x 5 x 5 = 2² x 5²
The common prime factors are 5², so the GCD is 5 x 5 = 25.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. Repeatedly divide the larger number by the smaller number and replace the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
100 ÷ 75 = 1 with a remainder of 25 75 ÷ 25 = 3 with a remainder of 0
The GCD is 25.
Once you've found the GCD (which is 25 in this case), divide both the numerator and the denominator by the GCD:
75 ÷ 25 = 3 100 ÷ 25 = 4
Therefore, 75/100 simplified to its lowest terms is 3/4.
Method 2: Simplifying Step-by-Step
If you don't immediately see the GCD, you can simplify the fraction step-by-step by dividing both the numerator and denominator by any common factor you notice. You'll repeat this process until no more common factors remain.
For example, with 75/100:
Both numbers are divisible by 5:
75 ÷ 5 = 15 100 ÷ 5 = 20
We now have 15/20. Both 15 and 20 are still divisible by 5:
15 ÷ 5 = 3 20 ÷ 5 = 4
This gives us the simplified fraction 3/4. This method takes more steps but is easier to grasp for beginners.
Understanding Equivalent Fractions
It's important to remember that simplifying a fraction doesn't change its value; it only changes its representation. 75/100, 15/20, and 3/4 all represent the same proportion or part of a whole. They are equivalent fractions. This concept is fundamental to understanding fractions and their manipulation in various mathematical operations.
Visual Representation
Imagine a pizza cut into 100 slices. 75/100 represents 75 slices out of 100. If you group those slices into sets of 25, you'll have 3 groups out of 4 possible groups, representing the simplified fraction 3/4. This visual approach helps solidify the understanding of equivalent fractions and the simplification process.
Practical Applications
The ability to simplify fractions is vital in numerous real-world scenarios:
- Cooking and Baking: Recipes often use fractions. Simplifying fractions makes it easier to measure ingredients accurately.
- Construction and Engineering: Precise measurements are crucial. Simplified fractions make calculations clearer and prevent errors.
- Finance and Budgeting: Understanding proportions and percentages relies heavily on fraction simplification.
- Data Analysis: Simplifying fractions helps in presenting data in a clear and concise manner.
Common Mistakes to Avoid
- Dividing only the numerator or denominator: Remember, you must divide both the numerator and the denominator by the same number to maintain the value of the fraction.
- Not finding the GCD: If you don't find the greatest common divisor, you might not reach the simplest form, requiring multiple steps.
- Incorrect prime factorization: Errors in prime factorization will lead to an incorrect GCD and an incorrectly simplified fraction.
Frequently Asked Questions (FAQ)
Q1: Is there a way to simplify fractions with very large numbers quickly?
A1: Yes, the Euclidean algorithm is a particularly efficient method for simplifying fractions with large numbers. Calculators and computer programs also offer functionalities to find the GCD and simplify fractions automatically.
Q2: Can a fraction be simplified if the numerator and denominator are prime numbers?
A2: No, if both the numerator and denominator are prime numbers (and different), the fraction is already in its simplest form, as their only common factor is 1.
Q3: What if the denominator is zero?
A3: A fraction with a zero denominator is undefined. Division by zero is not a valid mathematical operation.
Q4: How do I simplify fractions with negative numbers?
A4: Simplify the fraction as usual, ignoring the negative sign. Then, if only one of the numerator or denominator was negative, put the negative sign in front of the simplified fraction. If both were negative, the resulting fraction will be positive.
Q5: Are there any online tools to simplify fractions?
A5: Yes, many websites and applications provide fraction simplification tools that can automate the process. However, understanding the underlying principles is crucial to build strong mathematical skills.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill that enhances your understanding of mathematical concepts and enables you to tackle more complex problems with confidence. By mastering the methods outlined in this article – finding the GCD, simplifying step-by-step, and understanding equivalent fractions – you will be able to simplify any fraction efficiently and accurately. Remember that practice is key; the more you work with fractions, the more intuitive the process will become. Don't be afraid to experiment, make mistakes, and learn from them. With consistent effort, you'll develop a strong foundation in fractions and become proficient in simplifying them to their simplest form. The journey towards mathematical fluency is rewarding, and mastering fraction simplification is an important step along the way.
Latest Posts
Latest Posts
-
How Many Sacraments Are There
Sep 09, 2025
-
Of Mice And Men Slim
Sep 09, 2025
-
Another Word For Team Player
Sep 09, 2025
-
Map With Continents And Oceans
Sep 09, 2025
-
How Much Is 2000 Acres
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about 75/100 In Its Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.