7 2 As A Percentage
marihuanalabs
Sep 20, 2025 · 5 min read
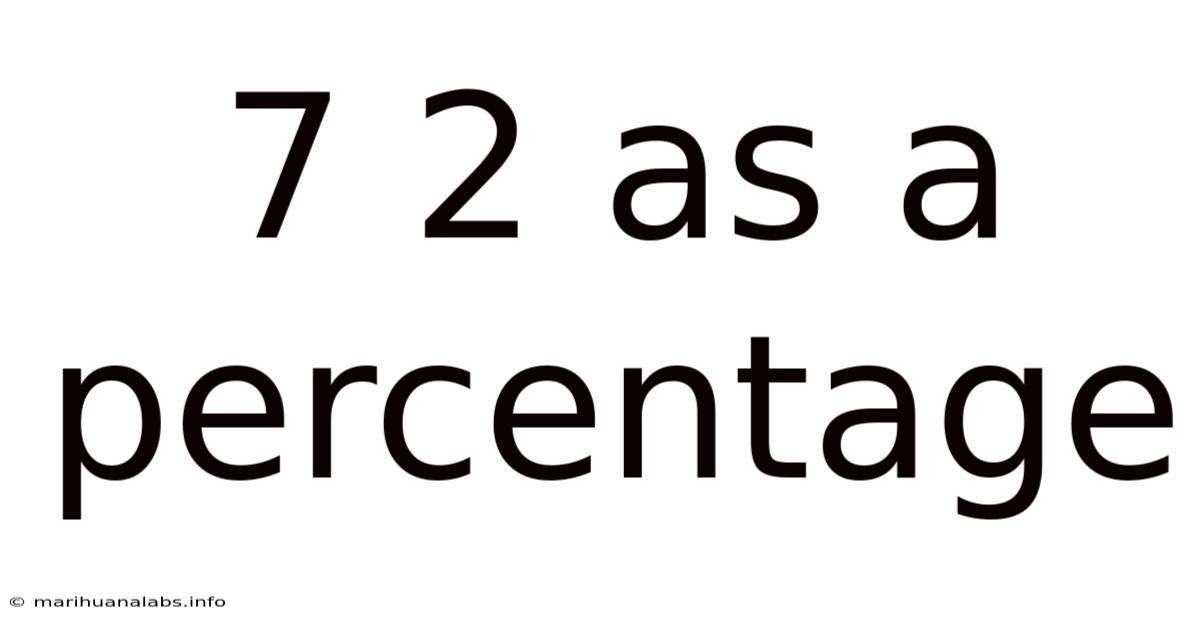
Table of Contents
Decoding 7/2 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, with applications spanning various fields from finance and statistics to everyday calculations. This comprehensive guide will delve into the process of converting the fraction 7/2 into a percentage, explaining the steps involved, providing insightful context, and exploring related concepts. We'll also tackle common misconceptions and answer frequently asked questions to solidify your understanding. By the end, you'll not only know the answer but also possess a deeper understanding of percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion of 7/2, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 7/2, 7 is the numerator and 2 is the denominator. This means we have 7 parts out of a whole that's divided into 2 equal parts.
A percentage, denoted by the symbol %, represents a fraction of 100. It expresses a proportion as a fraction of 100. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Percentages are commonly used to represent proportions, rates, and changes.
Converting 7/2 to a Percentage: A Step-by-Step Approach
Converting a fraction to a percentage involves two primary steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator. In our case:
7 ÷ 2 = 3.5
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
3.5 x 100 = 350
Therefore, 3.5 as a percentage is 350%.
Therefore, 7/2 as a percentage is 350%.
Understanding the Result: What Does 350% Mean?
A percentage greater than 100% indicates that the fraction represents more than one whole. In the case of 7/2, we have 3.5 wholes. This is because 7 is larger than the denominator 2. Think of it like this: if you have two pizzas, and you have 7 slices (assuming each pizza is divided into 2 slices), you have more than two whole pizzas. You have 3 and a half pizzas. This is why the percentage is greater than 100%.
Alternative Method: Using Proportions
Another way to approach this conversion is through proportions. We can set up a proportion to find the equivalent percentage:
7/2 = x/100
To solve for x (the percentage), we cross-multiply:
2x = 700
x = 700 ÷ 2
x = 350
This confirms our previous result: 7/2 is equal to 350%.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages is vital in various real-world scenarios:
- Finance: Calculating interest rates, profit margins, and returns on investment.
- Statistics: Representing data proportions and probabilities.
- Science: Expressing experimental results and measurements.
- Everyday life: Calculating discounts, tips, and sales tax.
Common Misconceptions and Pitfalls
A common mistake when working with fractions and percentages is confusing the concepts of part-to-whole and part-to-part. The fraction 7/2 represents a part-to-whole relationship (7 parts out of 2 parts), resulting in a percentage greater than 100%.
Another common error is forgetting to multiply the decimal by 100 when converting to a percentage. Remember that a percentage is always a fraction of 100.
Expanding Your Understanding: Working with Improper Fractions and Mixed Numbers
The fraction 7/2 is an improper fraction because the numerator (7) is larger than the denominator (2). Improper fractions can also be expressed as mixed numbers. A mixed number combines a whole number and a proper fraction.
To convert 7/2 to a mixed number, we divide the numerator by the denominator:
7 ÷ 2 = 3 with a remainder of 1
This means 7/2 can be written as the mixed number 3 1/2. This representation clarifies that we have 3 whole units and an additional half. Converting 3 1/2 to a decimal gives us 3.5, which, as shown earlier, is equivalent to 350%.
Further Exploration: Percentage Increase and Decrease
Understanding percentages allows for calculations involving percentage increases and decreases. For example, if a value increases by 350%, the new value is the original value multiplied by 4.5 (1 + 3.5). Conversely, calculating a percentage decrease requires understanding the context of the decrease in relation to the original value.
Frequently Asked Questions (FAQ)
Q: Can a percentage be greater than 100%?
A: Yes, a percentage can be greater than 100%. This indicates that the value is more than one whole.
Q: What is the easiest way to convert a fraction to a percentage?
A: The easiest way is to first convert the fraction to a decimal by dividing the numerator by the denominator, and then multiplying the decimal by 100 to express it as a percentage.
Q: What if the fraction has a decimal in the numerator or denominator?
A: Follow the same process: Divide the numerator by the denominator, and then multiply the resulting decimal by 100 to convert to a percentage.
Q: How can I check if my percentage conversion is correct?
A: You can check your answer by reversing the process: convert the percentage back to a decimal by dividing by 100, and then compare the decimal to the original fraction.
Conclusion
Converting 7/2 to a percentage provides a practical illustration of the fundamental principles of fraction-to-percentage conversions. The result, 350%, highlights the significance of understanding improper fractions and the interpretation of percentages greater than 100%. By mastering this skill, you gain a powerful tool applicable across various mathematical and real-world contexts. Remember to always focus on understanding the underlying concepts, not just memorizing procedures, to build a solid foundation in mathematics. This will enable you to approach any percentage calculation with confidence and accuracy.
Latest Posts
Latest Posts
-
What Is 5 Of 4000
Sep 20, 2025
-
London Bridge Is Falling Lyrics
Sep 20, 2025
-
American States Ending With A
Sep 20, 2025
-
Group 4 Elements Periodic Table
Sep 20, 2025
-
Resources And Types Of Resources
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 7 2 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.