7 12 As A Percent
marihuanalabs
Sep 07, 2025 · 6 min read
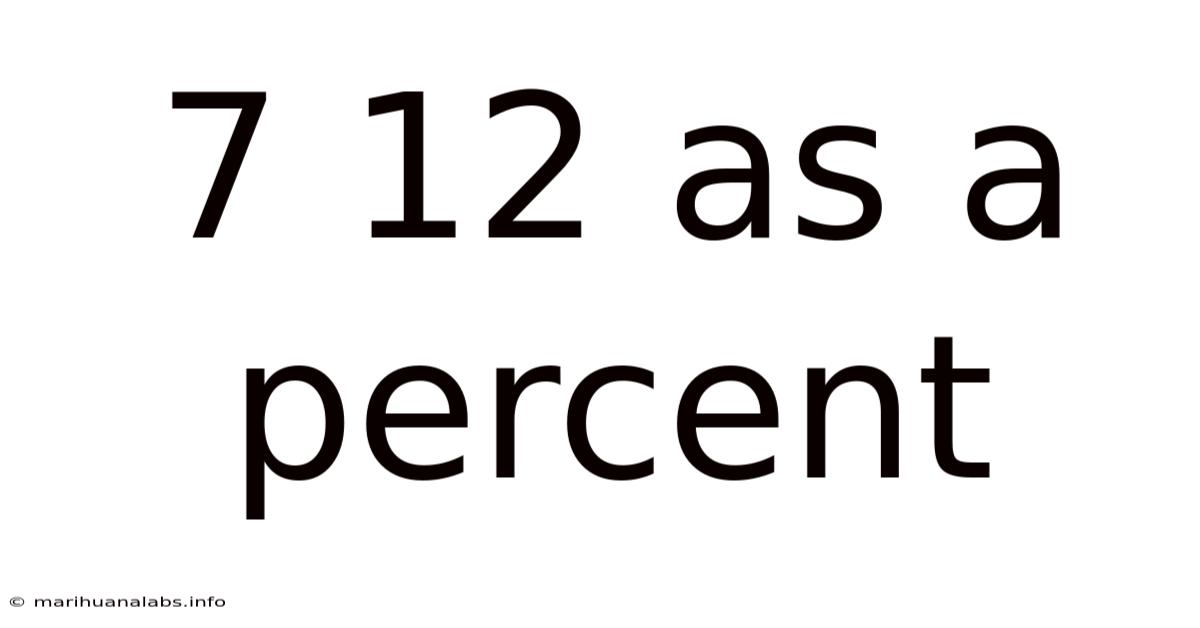
Table of Contents
7/12 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. This article delves deep into the process of converting the fraction 7/12 into a percentage, explaining the underlying concepts, providing step-by-step instructions, and exploring related mathematical ideas. We'll also address frequently asked questions and offer practical examples to solidify your understanding. By the end, you'll not only know the percentage equivalent of 7/12 but also possess a solid grasp of the broader concept of fraction-to-percentage conversion.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before we dive into the specifics of 7/12, let's clarify the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole. A fraction expresses a part of a whole using a numerator (the top number) and a denominator (the bottom number). A decimal represents a part of a whole using a base-ten system, with a decimal point separating the whole number from the fractional part. A percentage represents a part of a whole as a fraction of 100, denoted by the symbol %.
These three forms are interchangeable. For example, 1/2 is equivalent to 0.5 and 50%. Understanding their interconnectivity is key to mastering mathematical calculations.
Method 1: The Direct Conversion Method (Division and Multiplication)
The most straightforward method to convert 7/12 into a percentage involves two simple steps: division and multiplication.
Step 1: Divide the Numerator by the Denominator:
First, we divide the numerator (7) by the denominator (12):
7 ÷ 12 ≈ 0.583333...
The result is a decimal. Note that this decimal is a repeating decimal, meaning the digit 3 repeats infinitely. For practical purposes, we often round decimals to a specific number of decimal places.
Step 2: Multiply the Decimal by 100:
To convert the decimal to a percentage, we multiply the result by 100:
0.583333... × 100 ≈ 58.3333...%
Again, we have a repeating decimal. Rounding to two decimal places, we get approximately 58.33%.
Therefore, 7/12 is approximately equal to 58.33%.
Method 2: Using Equivalent Fractions
Another approach involves creating an equivalent fraction with a denominator of 100. This method avoids the use of decimals initially but might not always be easily achievable depending on the fraction.
To make the denominator 100, we need to find a number that, when multiplied by 12, gives 100 or a close approximation. Since 12 doesn't divide evenly into 100, we can use the decimal method for higher accuracy, but we can try to find a close approximation.
Let's find the closest fraction with 100 as the denominator:
While there isn't a perfect equivalent fraction, we can approximate it. Let's use a calculator to find a close approximation:
100 / 12 ≈ 8.333
Now, multiply both the numerator and the denominator of 7/12 by 8.333:
(7 × 8.333) / (12 × 8.333) ≈ 58.33/100
This shows us that 7/12 is approximately 58.33%. This method is less precise than the direct conversion method due to the approximation.
Method 3: Understanding the Concept of Percentage
A percentage is a way to express a proportion out of 100. To understand 7/12 as a percent more intuitively, imagine you have 12 equal parts of something (like a pizza sliced into 12 pieces). 7/12 means you have 7 out of those 12 parts. To express this as a percentage, we figure out what 7 represents as a proportion of 100. We already calculated that this is approximately 58.33%.
Practical Applications of 7/12 as a Percentage
Understanding the percentage equivalent of fractions like 7/12 has various practical applications:
-
Calculating discounts: Imagine a store offering a discount of 7/12 on an item. Knowing that this equates to approximately 58.33% off would allow you to easily calculate the final price.
-
Analyzing proportions: In statistics and data analysis, proportions are often expressed as percentages. If 7 out of 12 students passed a test, understanding this as 58.33% passing rate provides a clearer picture.
-
Financial calculations: Interest rates, investment returns, and other financial calculations often involve converting fractions to percentages.
-
Everyday percentages: Numerous everyday scenarios involve calculating percentages, such as figuring out sales tax, tips, or the percentage of a task completed.
Addressing Frequently Asked Questions (FAQs)
Q1: Why is the percentage of 7/12 an approximation?
A1: The decimal representation of 7/12 (0.583333...) is a repeating decimal. We must round the decimal to a certain number of decimal places to obtain a practical percentage value. This rounding introduces a slight approximation.
Q2: How can I improve the accuracy of the percentage?
A2: The accuracy depends on the number of decimal places you use during the calculation. Using more decimal places in your calculations will yield a more precise result, but for most practical purposes, rounding to two decimal places is sufficient.
Q3: Are there other fractions that are difficult to convert to percentages?
A3: Yes, any fraction whose decimal equivalent is a repeating decimal will require rounding when converting to a percentage. Fractions with denominators that are not factors of 100 (or multiples of 100) will often result in repeating decimals.
Q4: What if the fraction is an improper fraction (numerator > denominator)?
A4: The process remains the same. Divide the numerator by the denominator, and then multiply the result by 100 to find the percentage. For example, if we had the improper fraction 13/12, we would divide 13 by 12 (≈ 1.0833) and then multiply by 100 (≈ 108.33%). The result will be a percentage greater than 100%.
Q5: Can I use a calculator for this conversion?
A5: Yes, using a calculator significantly simplifies the process. Simply divide the numerator by the denominator and then multiply the result by 100 to obtain the percentage. Many calculators have a percentage function that automates this calculation.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a fundamental skill with numerous real-world applications. While the process might seem daunting at first, understanding the underlying principles—the interconnectedness of fractions, decimals, and percentages—makes it significantly easier. Whether using the direct division method or the equivalent fraction approach (though less precise in this case), the goal is to determine the proportion represented by the fraction in relation to 100. Remember that for fractions like 7/12, the resulting percentage will often be an approximation due to repeating decimals, and the level of precision depends on the number of decimal places retained in the calculation. With practice, you'll be able to perform these conversions quickly and confidently. This understanding empowers you to tackle more complex mathematical problems and confidently navigate various real-world scenarios requiring percentage calculations.
Latest Posts
Latest Posts
-
What Is 20 Of 120
Sep 07, 2025
-
What Time In Malta Now
Sep 07, 2025
-
Far Better Thing I Do
Sep 07, 2025
-
Unit Of Rate Of Flow
Sep 07, 2025
-
Quotes From The Book Matilda
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about 7 12 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.