5 Divided By 1 4
marihuanalabs
Sep 11, 2025 · 5 min read
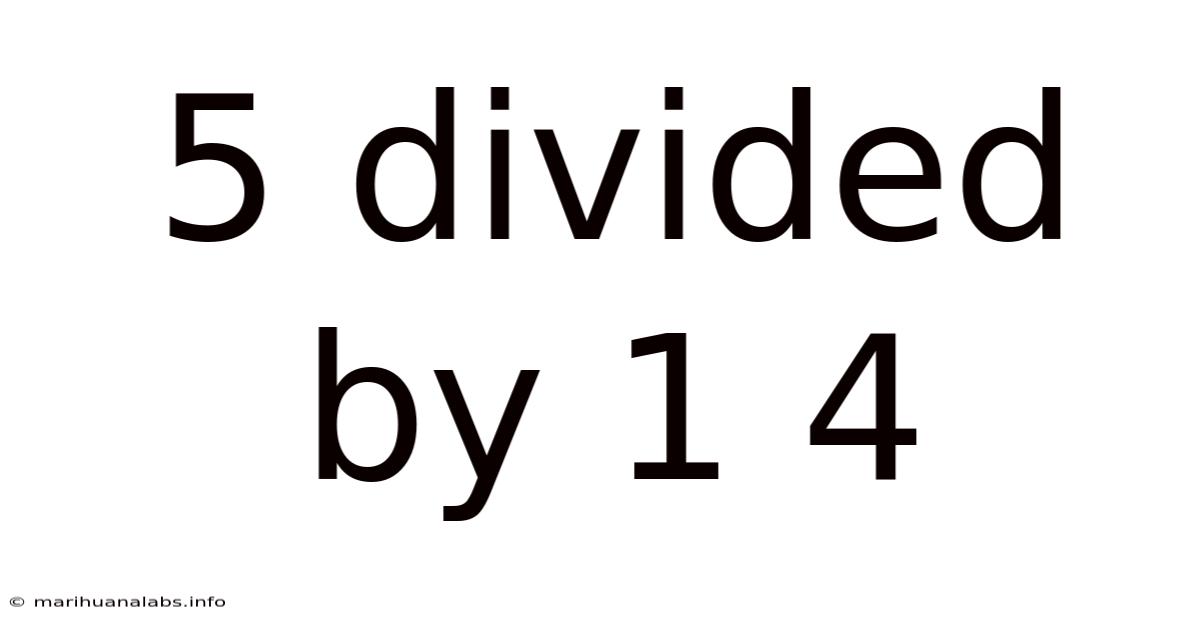
Table of Contents
Decoding 5 Divided by 1/4: A Comprehensive Guide to Fraction Division
Understanding fraction division can be a stumbling block for many, but mastering it unlocks a world of mathematical possibilities. This comprehensive guide will delve into the intricacies of dividing 5 by 1/4, explaining the process step-by-step, providing the scientific rationale behind the method, and addressing frequently asked questions. We'll explore this seemingly simple problem in depth, revealing the underlying concepts and empowering you to tackle similar problems with confidence.
Introduction: Understanding the Problem
The question "5 divided by 1/4" (often written as 5 ÷ 1/4 or 5 / (1/4)) might seem straightforward at first glance. However, it highlights a crucial concept in arithmetic: dividing by a fraction is equivalent to multiplying by its reciprocal. This seemingly simple problem offers a gateway to understanding the fundamental principles of fraction manipulation and division. This article will not only provide the solution but also a deep understanding of the why behind the process.
Step-by-Step Solution: From Division to Multiplication
The key to solving 5 ÷ 1/4 lies in understanding the reciprocal. The reciprocal of a fraction is simply the fraction inverted. For example, the reciprocal of 1/4 is 4/1 (or simply 4).
Here's the step-by-step solution:
-
Rewrite the division as multiplication: Instead of dividing by 1/4, we multiply by its reciprocal, 4. So, 5 ÷ 1/4 becomes 5 x 4.
-
Perform the multiplication: Multiplying 5 by 4 is a simple operation: 5 x 4 = 20.
Therefore, 5 divided by 1/4 equals 20.
Visualizing the Solution: A Practical Approach
Imagine you have 5 pizzas, and you want to divide each pizza into quarters (1/4). How many slices do you have in total?
- Each pizza yields 4 slices (because 1 whole pizza is equal to 4/4).
- With 5 pizzas, you'll have 5 x 4 = 20 slices.
This visual representation helps solidify the concept. Dividing by a fraction less than one (like 1/4) results in a larger number than the original because you're essentially finding how many parts of that fraction are contained within the whole number.
The Mathematical Rationale: Reciprocal and Division
The method of converting division by a fraction into multiplication by its reciprocal is rooted in the fundamental properties of fractions and division.
-
Division as the inverse of multiplication: Division is the inverse operation of multiplication. When we divide a by b (a ÷ b), we're essentially asking "what number, when multiplied by b, equals a?"
-
The multiplicative inverse (reciprocal): The reciprocal of a number is the number that, when multiplied by the original number, equals 1. For fractions, the reciprocal is found by simply inverting the numerator and denominator.
-
Connecting division and reciprocals: To understand why we multiply by the reciprocal when dividing by a fraction, consider the following:
(a ÷ (b/c)) = (a/1) x (c/b) = (a x c) / (1 x b) = (a x c) / b
This demonstrates that dividing by a fraction (b/c) is equivalent to multiplying by its reciprocal (c/b). This holds true regardless of the values of a, b, and c, provided that b and c are not zero.
Extending the Concept: More Complex Fraction Division Problems
The principles discussed above can be applied to more complex fraction division problems. For instance, let's consider dividing 3/5 by 2/7:
-
Find the reciprocal of the divisor: The reciprocal of 2/7 is 7/2.
-
Convert the division to multiplication: 3/5 ÷ 2/7 becomes 3/5 x 7/2.
-
Perform the multiplication: (3 x 7) / (5 x 2) = 21/10. This can be simplified as 2 1/10.
This showcases the versatility and power of the reciprocal method for handling various fraction division problems.
Addressing Common Misconceptions
Many learners struggle with fraction division due to a few common misconceptions:
-
Incorrectly multiplying by the original fraction: Some students mistakenly multiply by the original fraction instead of its reciprocal, leading to incorrect results. Remember, the reciprocal is essential.
-
Difficulty in simplifying fractions: While the multiplication is relatively simple, simplifying the resulting fraction can be challenging. Practice with simplifying fractions will improve accuracy and efficiency.
-
Confusion with addition and subtraction of fractions: The rules for adding and subtracting fractions are different from those for multiplication and division. Keep these operations separate in your understanding.
Frequently Asked Questions (FAQ)
Q: Why do we use reciprocals in fraction division?
A: We use reciprocals because division is the inverse operation of multiplication. Multiplying by the reciprocal effectively "undoes" the division by the original fraction.
Q: Can I divide a whole number by a fraction using a different method?
A: While the reciprocal method is most efficient, you could conceptually divide the whole number into parts equal to the denominator of the fraction. However, this becomes cumbersome for larger numbers.
Q: What if the fraction I'm dividing by is an improper fraction (numerator larger than the denominator)?
A: The same principle applies. Find the reciprocal of the improper fraction (invert it), and then multiply.
Q: How can I improve my understanding of fraction division?
A: Practice is key. Start with simple problems and gradually work towards more complex ones. Visual representations (like the pizza example) and repeated practice will solidify your understanding.
Conclusion: Mastering Fraction Division
Understanding the division of whole numbers by fractions is fundamental to many mathematical concepts. The seemingly simple problem of 5 divided by 1/4 illustrates a powerful and versatile technique – converting division by a fraction into multiplication by its reciprocal. By mastering this technique and understanding the underlying mathematical principles, you'll build a solid foundation for tackling more complex mathematical challenges. Remember to practice consistently, and don't hesitate to revisit the steps and explanations provided here to reinforce your learning. The more you engage with the concepts, the clearer and more intuitive fraction division will become.
Latest Posts
Latest Posts
-
How Many Ounces Is 500ml
Sep 11, 2025
-
Venus De Milo Liberty Bell
Sep 11, 2025
-
The Flowers By Alice Walker
Sep 11, 2025
-
Island Of The Dolphins Book
Sep 11, 2025
-
Cold Blooded Vs Warm Blooded
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 1 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.