5 9 Divided By 5
marihuanalabs
Sep 18, 2025 · 6 min read
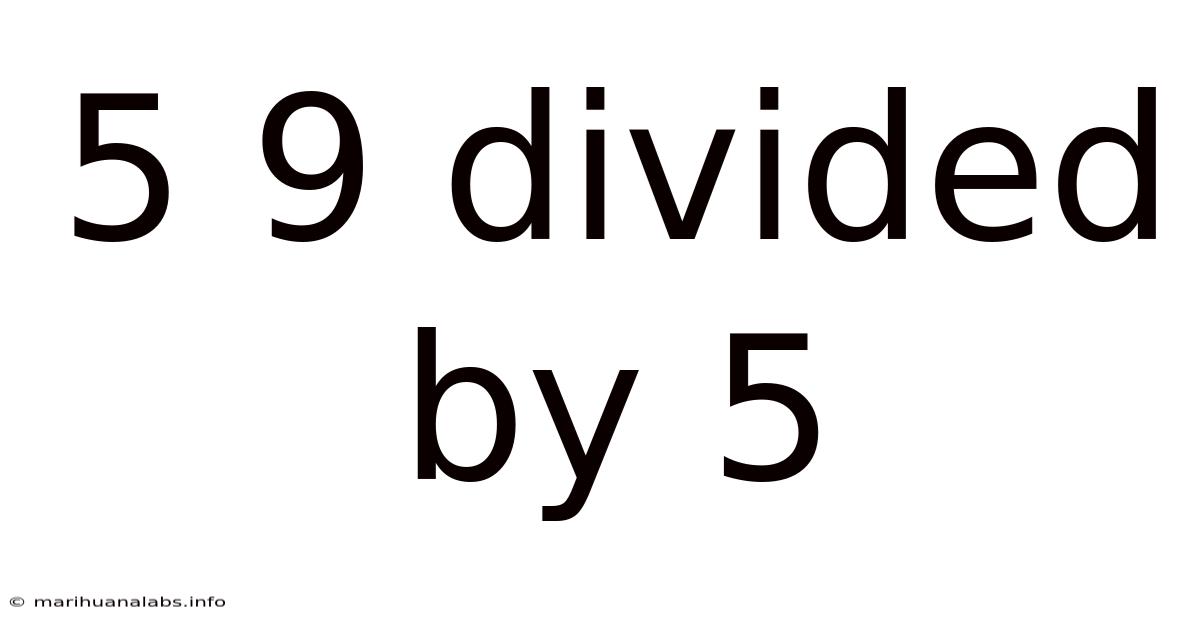
Table of Contents
Unpacking 59 Divided by 5: A Deep Dive into Division and Beyond
This article explores the seemingly simple calculation of 59 divided by 5, but delves far deeper than just finding the answer. We'll uncover the underlying principles of division, explore different methods for solving the problem, discuss the significance of remainders, and touch upon the broader mathematical concepts connected to this seemingly straightforward operation. This comprehensive guide is designed for learners of all levels, from elementary school students grasping the basics to those looking for a refresher on fundamental arithmetic. Understanding this single division problem unlocks a wealth of mathematical understanding.
Understanding the Basics of Division
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the context of 59 divided by 5 (written as 59 ÷ 5 or 59/5), we're asking: "How many times does 5 go into 59?"
The number being divided (59) is called the dividend. The number we're dividing by (5) is the divisor. The result of the division is the quotient, and any amount left over is the remainder.
Method 1: Long Division
Long division is a systematic method for performing division, particularly useful for larger numbers. Let's break down 59 ÷ 5 using this approach:
-
Set up the problem: Write the dividend (59) inside the long division symbol ( ⟌ ) and the divisor (5) outside.
_____ 5 | 59 -
Divide the tens digit: How many times does 5 go into 5 (the tens digit of 59)? It goes in once (1). Write the 1 above the 5 in the dividend.
1____ 5 | 59 -
Multiply and subtract: Multiply the quotient (1) by the divisor (5): 1 x 5 = 5. Subtract this from the tens digit of the dividend: 5 - 5 = 0.
1____ 5 | 59 5 - 0 -
Bring down the ones digit: Bring down the ones digit of the dividend (9) next to the 0.
1____ 5 | 59 5 - 09 -
Divide the ones digit: How many times does 5 go into 9? It goes in once (1) with a remainder. Write the 1 above the 9.
11___ 5 | 59 5 - 09 -
Multiply and subtract: Multiply the quotient (1) by the divisor (5): 1 x 5 = 5. Subtract this from 9: 9 - 5 = 4. This is the remainder.
11___ 5 | 59 5 - 09 5 - 4
Therefore, 59 ÷ 5 = 11 with a remainder of 4. We can express this as 11 R 4.
Method 2: Repeated Subtraction
Repeated subtraction is a more intuitive method, particularly helpful for visualizing the process of division. We repeatedly subtract the divisor (5) from the dividend (59) until we reach a number less than the divisor. The number of times we subtract represents the quotient, and the remaining number is the remainder.
-
Start with the dividend: 59
-
Subtract the divisor repeatedly:
- 59 - 5 = 54
- 54 - 5 = 49
- 49 - 5 = 44
- 44 - 5 = 39
- 39 - 5 = 34
- 34 - 5 = 29
- 29 - 5 = 24
- 24 - 5 = 19
- 19 - 5 = 14
- 14 - 5 = 9
- 9 - 5 = 4
-
Count the subtractions: We subtracted 5 eleven times. This is our quotient (11).
-
The remainder: The number left after the last subtraction is 4. This is our remainder.
Therefore, using repeated subtraction, we again arrive at the answer: 59 ÷ 5 = 11 with a remainder of 4.
Method 3: Fractions and Decimals
Division can also be represented as a fraction. 59 ÷ 5 is equivalent to the fraction 59/5. This fraction can be expressed as a mixed number or a decimal.
-
Mixed Number: To convert the improper fraction 59/5 into a mixed number, we divide 59 by 5. The quotient (11) becomes the whole number part, and the remainder (4) becomes the numerator of the fraction, with the divisor (5) as the denominator. So, 59/5 = 11 4/5.
-
Decimal: To express the fraction as a decimal, we perform the long division as shown in Method 1, but continue the process beyond the whole number portion. After subtracting 5 from 9 (leaving a remainder of 4), we add a decimal point and a zero to the dividend, bringing it down as 40. Then we divide 40 by 5, obtaining 8. Thus, 59/5 = 11.8.
The Significance of the Remainder
The remainder (4 in this case) is a crucial part of the answer. It signifies the portion of the dividend that couldn't be evenly divided by the divisor. In real-world scenarios, understanding the remainder is often essential. For example, if you have 59 candies to distribute equally among 5 friends, each friend would get 11 candies, and you'd have 4 candies left over.
Applications and Further Exploration
The simple division of 59 by 5 opens doors to a vast landscape of mathematical concepts. Here are some examples:
-
Real-world problem-solving: From dividing costs among friends to calculating the number of items needed for a project, division is fundamental in daily life.
-
Algebra: Understanding division is essential for solving algebraic equations and manipulating variables.
-
Geometry: Calculating areas, volumes, and other geometric properties often involves division.
-
Statistics: Analyzing data and calculating averages requires a strong understanding of division.
-
Computer Science: Division plays a crucial role in various algorithms and data structures.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve 59 ÷ 5? A: Yes, a calculator provides a quick and efficient way to find the answer, typically displaying 11.8.
-
Q: What if the remainder is zero? A: If the remainder is zero, it means the division is exact, and the dividend is perfectly divisible by the divisor.
-
Q: How important is it to understand different methods of division? A: Understanding multiple methods improves your mathematical flexibility and deepens your conceptual understanding. It allows you to choose the method best suited to a particular problem or situation.
-
Q: What are some common mistakes to avoid when performing division? A: Common mistakes include misplacing digits during long division, incorrectly handling remainders, and forgetting to consider the decimal point when expressing the result as a decimal.
Conclusion
The seemingly simple problem of 59 divided by 5 offers a rich opportunity to explore the fundamentals of division and its broader applications. By understanding the different methods—long division, repeated subtraction, and the use of fractions and decimals—we gain a deeper appreciation for the intricacies of this essential mathematical operation. Remember the significance of the remainder and how it relates to real-world problem-solving. Mastering division is a cornerstone of mathematical proficiency, leading to success in more advanced mathematical concepts and applications across various fields. Keep practicing, and you'll find that the seemingly simple calculations become stepping stones to greater mathematical understanding and confidence.
Latest Posts
Latest Posts
-
Murder Is Announced Miss Marple
Sep 18, 2025
-
Adding Subtracting Fractions Different Denominators
Sep 18, 2025
-
Batten Down The Hatches Origin
Sep 18, 2025
-
Should The West Be Capitalized
Sep 18, 2025
-
Peter And The Wolf Instruments
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 5 9 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.