5 7 As A Percentage
marihuanalabs
Sep 23, 2025 · 5 min read
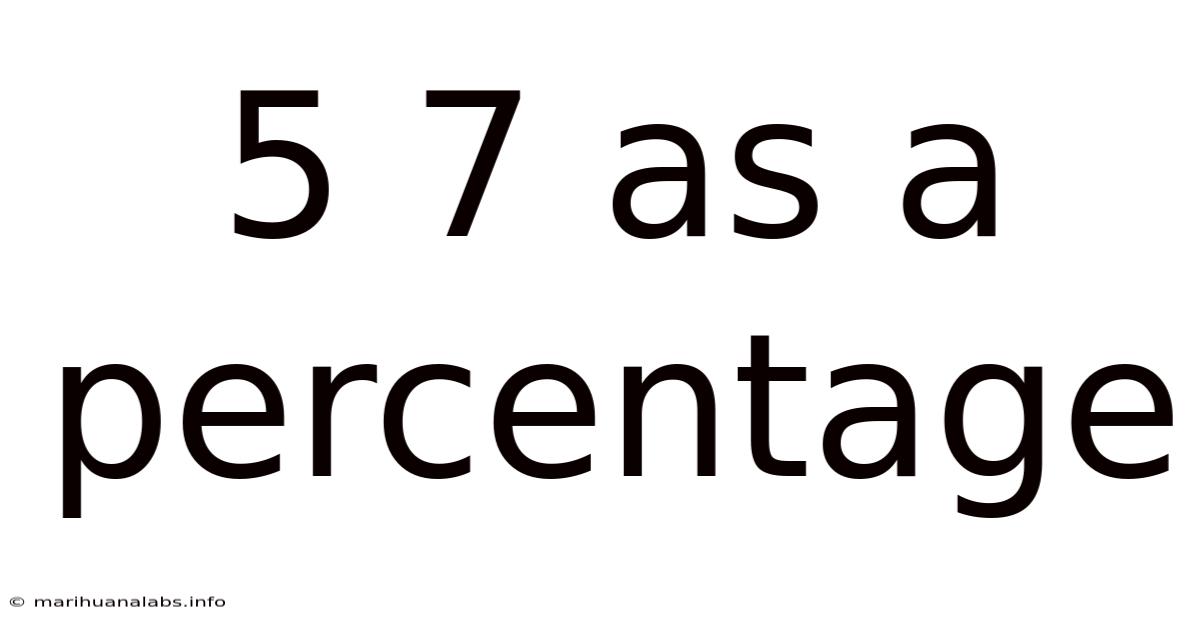
Table of Contents
Decoding 5/7 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, crucial for everyday life and various professional fields. This article delves deep into converting the fraction 5/7 into a percentage, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing frequently asked questions. We will also examine the practical applications of this conversion and offer strategies for similar calculations. By the end, you'll not only know the percentage equivalent of 5/7 but also gain a comprehensive understanding of fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before we dive into converting 5/7, let's solidify our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into.
A percentage, on the other hand, represents a fraction of 100. The term "percent" literally means "out of 100." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 5/7 to a Percentage: Step-by-Step
Converting a fraction to a percentage involves two main steps:
-
Divide the numerator by the denominator: This gives us the decimal equivalent of the fraction.
In the case of 5/7, we divide 5 by 7:
5 ÷ 7 ≈ 0.7142857
-
Multiply the decimal by 100: This converts the decimal to a percentage.
0.7142857 × 100 ≈ 71.42857%
Therefore, 5/7 is approximately 71.43%. We often round percentages to two decimal places for practicality.
A Deeper Dive into the Calculation
The conversion process relies on the fundamental relationship between fractions, decimals, and percentages. Essentially, we're expressing the same quantity in different forms. The division step transforms the fraction into a decimal, representing the fractional part as a proportion of one. Multiplying by 100 scales this proportion to represent it as parts per hundred – the definition of a percentage.
Let's break down the calculation further:
- 5/7: This represents five parts out of a total of seven equal parts.
- 0.7142857: This decimal representation shows that for every one whole unit, we have approximately 0.7142857 of that unit.
- 71.42857%: This percentage representation expresses the same proportion as 71.42857 parts out of 100.
The slight discrepancy arises because 5/7 is a rational number with a non-terminating decimal expansion. This means its decimal representation continues infinitely without repeating in a predictable pattern. Rounding becomes necessary for practical application.
Practical Applications of 5/7 as a Percentage
The ability to convert fractions to percentages has numerous real-world applications:
-
Calculating Grades: Imagine a student scoring 5 out of 7 questions correctly on a quiz. Converting 5/7 to approximately 71.43% provides a clear and easily understandable representation of their performance.
-
Analyzing Data: In various fields, from business to science, data is often presented as fractions or ratios. Converting these to percentages allows for easier comparison and interpretation. For instance, if 5 out of 7 customers are satisfied with a product, that equates to approximately 71.43% customer satisfaction.
-
Financial Calculations: Percentages are widely used in financial calculations, including interest rates, discounts, and profit margins. Understanding fraction-to-percentage conversions is essential for making informed financial decisions.
-
Everyday Life: From calculating tips in restaurants to understanding sales discounts, percentage calculations are commonplace in everyday situations. A strong understanding of these conversions simplifies these tasks.
Alternative Methods for Calculating Percentages
While the method described above is the most straightforward, there are alternative approaches to convert fractions to percentages:
-
Using a Calculator: Most calculators have a percentage function that directly converts fractions to percentages. Simply input the fraction (5/7) and use the percentage function. This is a quick and efficient method.
-
Using Proportions: You can set up a proportion to solve for the percentage:
5/7 = x/100
Cross-multiplying, we get:
7x = 500
Solving for x:
x = 500/7 ≈ 71.43
This method demonstrates the underlying mathematical relationship between fractions and percentages.
Frequently Asked Questions (FAQs)
Q: Is there a way to convert 5/7 to a percentage without using a calculator?
A: Yes, long division is required, as described in the "Converting 5/7 to a Percentage: Step-by-Step" section. While it might be slightly more time-consuming, it allows you to understand the underlying process.
Q: Why is the percentage approximation, and not an exact value?
A: 5/7 is a rational number with a non-terminating, non-repeating decimal expansion. This means its decimal representation goes on infinitely. Therefore, we round the result to a practical number of decimal places (typically two) for ease of use.
Q: How can I improve my skills in converting fractions to percentages?
A: Practice is key! Try converting various fractions to percentages. Start with simple fractions and gradually move to more complex ones. You can find practice problems online or in math textbooks.
Q: Are there any online tools to help with this conversion?
A: While I cannot provide direct links, a quick search for "fraction to percentage calculator" will provide numerous online tools that can perform this conversion for you. These tools can be helpful for checking your work or for quick conversions.
Conclusion
Converting 5/7 to a percentage is a fundamental mathematical skill with far-reaching applications. This article has provided a comprehensive guide, detailing the step-by-step process, explaining the underlying principles, and exploring various practical applications. Understanding this conversion not only enhances your mathematical abilities but also equips you with a crucial tool for navigating various aspects of life and various professional fields. By mastering this skill, you'll confidently handle percentage calculations in diverse contexts, from everyday tasks to complex analytical situations. Remember that practice and understanding the fundamental principles are vital for mastering any mathematical concept.
Latest Posts
Latest Posts
-
Gcf Of 98 And 42
Sep 23, 2025
-
Brave New World Book Cover
Sep 23, 2025
-
What Is A Humiliation Ritual
Sep 23, 2025
-
Features Of A Letter Ks1
Sep 23, 2025
-
Can Botox Cause Bells Palsy
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 7 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.