5 20 As A Percent
marihuanalabs
Sep 22, 2025 · 5 min read
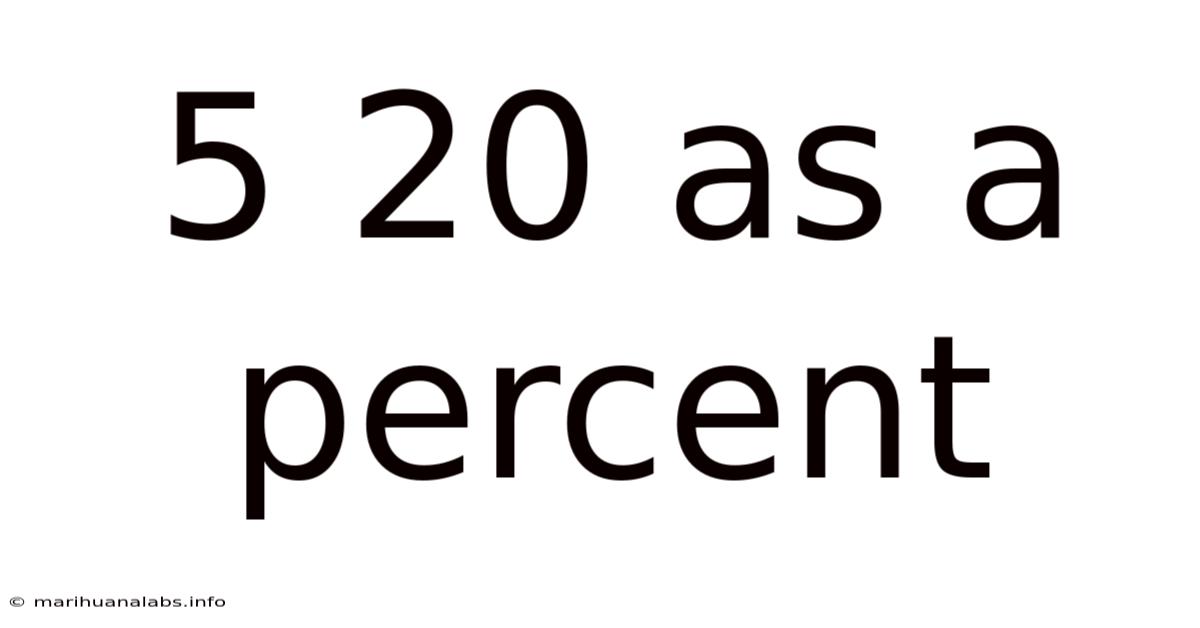
Table of Contents
Decoding 5/20 as a Percentage: A Comprehensive Guide
Understanding fractions and percentages is fundamental to various aspects of life, from calculating discounts in a store to comprehending financial reports. This article will delve deep into converting the fraction 5/20 into a percentage, explaining the process step-by-step, exploring the underlying mathematical principles, and providing practical applications to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions about percentage calculations. By the end, you'll not only know the percentage equivalent of 5/20 but also possess a robust understanding of the concepts involved.
Understanding Fractions and Percentages
Before we tackle 5/20, let's establish a solid foundation. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts.
A percentage, on the other hand, expresses a fraction as a portion of 100. The term "percent" literally means "per hundred." So, 25% means 25 out of 100, or 25/100. Percentages are a convenient way to compare and represent proportions.
Converting 5/20 to a Percentage: A Step-by-Step Approach
There are two primary methods to convert the fraction 5/20 into a percentage:
Method 1: Simplifying the Fraction First
This method involves simplifying the fraction to its lowest terms before converting to a percentage. This often makes the calculation easier.
-
Simplify the Fraction: We can simplify 5/20 by finding the greatest common divisor (GCD) of both the numerator (5) and the denominator (20). The GCD of 5 and 20 is 5. Dividing both the numerator and the denominator by 5, we get:
5 ÷ 5 / 20 ÷ 5 = 1/4
-
Convert to a Decimal: To convert the simplified fraction 1/4 to a decimal, divide the numerator (1) by the denominator (4):
1 ÷ 4 = 0.25
-
Convert to a Percentage: Multiply the decimal by 100 to express it as a percentage:
0.25 × 100 = 25%
Therefore, 5/20 is equal to 25%.
Method 2: Direct Conversion
This method involves directly converting the fraction to a decimal and then to a percentage without simplifying the fraction first.
-
Convert to a Decimal: Divide the numerator (5) by the denominator (20):
5 ÷ 20 = 0.25
-
Convert to a Percentage: Multiply the decimal by 100:
0.25 × 100 = 25%
As you can see, both methods yield the same result: 25%. Choosing the method that best suits your comfort level is perfectly acceptable.
The Mathematical Principle Behind Percentage Conversion
The core principle behind converting a fraction to a percentage lies in the concept of proportionality. A percentage expresses a fraction as a proportion of 100. Therefore, to convert any fraction to a percentage, we essentially solve the proportion:
Fraction/1 = Percentage/100
For 5/20:
5/20 = x/100
To solve for x (the percentage), we cross-multiply:
20x = 500
x = 500/20
x = 25
Therefore, 5/20 is equivalent to 25%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous everyday situations:
-
Discounts and Sales: Stores often advertise discounts as percentages (e.g., "20% off"). Calculating the actual discount amount requires converting the percentage to a decimal and multiplying it by the original price.
-
Taxes: Sales tax and income tax are expressed as percentages. Knowing how to calculate these percentages is vital for budgeting and financial planning.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Grades and Test Scores: Academic performance is often expressed as percentages, allowing for easy comparison of performance across different assessments.
-
Data Analysis: Percentages are widely used in data analysis to represent proportions and trends in data sets. This is essential in fields like market research, statistics, and scientific studies.
Common Misconceptions about Percentages
Several common misconceptions surround percentages:
-
Adding Percentages Directly: You cannot simply add percentages directly unless they are of the same whole. For example, a 10% increase followed by a 10% decrease does not result in a net change of 0%.
-
Percentage Increase vs. Percentage Decrease: The calculations for percentage increase and decrease are slightly different. A percentage increase is calculated based on the original value, while a percentage decrease is calculated based on the new, decreased value.
-
Confusion with Decimal Places: Mistakes often occur due to incorrect handling of decimal places when converting between decimals and percentages. Always double-check your calculations to avoid errors.
Frequently Asked Questions (FAQs)
Q: Can I convert any fraction to a percentage?
A: Yes, any fraction can be converted to a percentage by dividing the numerator by the denominator and multiplying by 100.
Q: What if the percentage calculation results in a decimal value?
A: You can round the decimal value to the nearest whole number or leave it as a decimal, depending on the level of precision required.
Q: Are there any online tools or calculators that can help with percentage conversions?
A: Yes, many online calculators are available that can easily convert fractions to percentages. However, understanding the underlying principles is crucial for problem-solving and critical thinking.
Q: Why is understanding percentages important in everyday life?
A: Percentages are used in various aspects of life, from finance and shopping to academics and data analysis. A solid grasp of percentages empowers you to make informed decisions and navigate various situations effectively.
Conclusion
Converting 5/20 to a percentage (25%) is a straightforward process, but understanding the underlying principles of fractions and percentages is crucial for broader applications. This article has provided a comprehensive guide, highlighting different methods, addressing common misconceptions, and demonstrating practical uses. By mastering these concepts, you'll be better equipped to handle various mathematical challenges and make informed decisions in your daily life. Remember, practice is key to building confidence and fluency in percentage calculations. So, grab a few more fraction problems and put your newfound knowledge to the test!
Latest Posts
Latest Posts
-
Quotes About A Guilty Conscience
Sep 22, 2025
-
Formula For Calculating Unit Cost
Sep 22, 2025
-
Nobleman Crossword Clue 5 Letters
Sep 22, 2025
-
Turning Point Of Quadratic Function
Sep 22, 2025
-
Animals On The Forest Floor
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 5 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.