4 6 As A Percent
marihuanalabs
Sep 07, 2025 · 5 min read
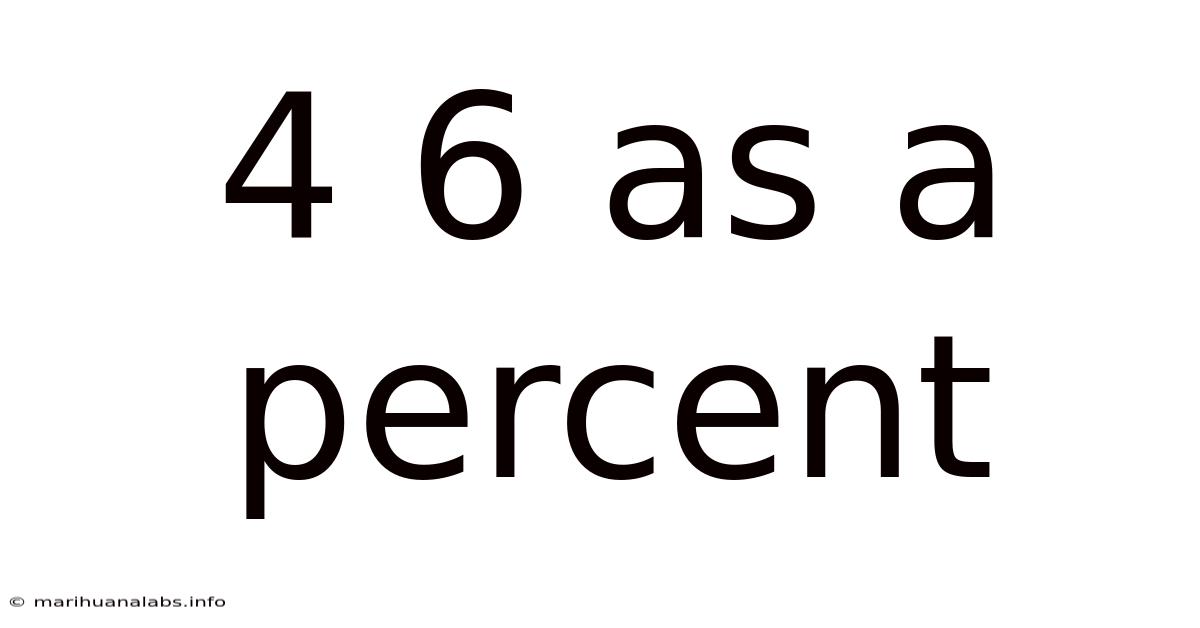
Table of Contents
Understanding 4/6 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, crucial for everyday life and various professional fields. This comprehensive guide will delve into the process of converting the fraction 4/6 into a percentage, exploring the underlying concepts and providing practical examples. We'll cover the calculation method, simplification techniques, real-world applications, and frequently asked questions, ensuring a thorough understanding of this important mathematical concept.
Introduction: From Fractions to Percentages
A fraction represents a part of a whole. For instance, 4/6 signifies four parts out of a total of six equal parts. A percentage, on the other hand, expresses a fraction as parts per hundred. Converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100. This process is essential for comparing different fractions, making calculations easier, and representing data in a more readily understandable format. This article will focus specifically on converting 4/6 to a percentage, demonstrating various methods and offering insights into the underlying mathematical principles.
Method 1: Simplifying the Fraction Before Conversion
Before diving into the percentage calculation, it's often beneficial to simplify the fraction. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator (top number) and the denominator (bottom number) by their greatest common divisor (GCD).
In the case of 4/6, the GCD of 4 and 6 is 2. Dividing both the numerator and denominator by 2 gives us:
4 ÷ 2 = 2 6 ÷ 2 = 3
Therefore, 4/6 simplifies to 2/3. This simplified fraction is equivalent to the original fraction and makes the subsequent percentage calculation easier.
Method 2: Converting the Simplified Fraction to a Percentage
Now that we have the simplified fraction 2/3, we can convert it to a percentage. There are two primary methods for this:
- Method 2a: Using Division
To convert a fraction to a percentage, divide the numerator by the denominator and then multiply the result by 100. Applying this to 2/3:
2 ÷ 3 ≈ 0.6667
0.6667 x 100 = 66.67%
Therefore, 2/3 (and equivalently 4/6) is approximately 66.67%. The recurring decimal 0.6667 is often rounded to two decimal places for practical purposes.
- Method 2b: Finding an Equivalent Fraction with a Denominator of 100
Alternatively, we can find an equivalent fraction with a denominator of 100. To do this, we need to find a number that, when multiplied by the denominator (3), equals 100. This is not a whole number in this case, highlighting the advantage of Method 2a for fractions that don't easily convert to a denominator of 100. Let's demonstrate this method with a different fraction for clarity.
Let's say we have the fraction 1/4. To find its percentage equivalent, we can multiply both the numerator and the denominator by 25 (because 4 x 25 = 100):
(1 x 25) / (4 x 25) = 25/100
Since 25/100 represents 25 parts out of 100, this fraction is equal to 25%.
Method 3: Direct Conversion of 4/6 to a Percentage (Without Simplification)
While simplifying the fraction is generally recommended, we can also directly convert 4/6 to a percentage using the division method:
4 ÷ 6 ≈ 0.6667
0.6667 x 100 = 66.67%
This demonstrates that whether you simplify the fraction first or not, the final percentage result remains the same.
Understanding the Recurring Decimal:
The result 66.67% includes a recurring decimal (0.666...). This means the decimal part continues infinitely with the digit 6. In practical applications, rounding to a suitable number of decimal places (e.g., two decimal places) is necessary. However, it's important to remember that the exact value is not 66.67%, but rather 66.666...% which continues infinitely.
Real-World Applications of Percentage Conversions
Understanding how to convert fractions to percentages is essential in numerous real-world scenarios:
- Calculating Grades: If you answered 4 out of 6 questions correctly on a test, your score is 66.67%.
- Financial Calculations: Percentages are used extensively in finance, such as calculating interest rates, discounts, and profit margins.
- Data Analysis: Representing data as percentages makes it easier to compare and interpret different datasets.
- Scientific Measurements: Percentages are used to express concentrations, error margins, and other quantitative measurements in scientific fields.
- Everyday Life: Sales discounts, tax rates, and tip calculations all involve percentage calculations.
Further Exploration: Percentages and Proportions
The concept of percentage is intrinsically linked to the concept of proportion. A proportion is a statement that two ratios are equal. The fraction 4/6 can be expressed as a proportion:
4/6 = x/100
To solve for x (the percentage), we can cross-multiply:
6x = 400
x = 400/6 = 66.67
This method reinforces the connection between fractions, proportions, and percentages.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to simplify fractions before converting to percentages?
- A: Simplifying fractions makes the calculation easier and reduces the risk of errors, especially when dealing with larger numbers. It also helps to understand the relationship between the numerator and the denominator more clearly.
-
Q: What if the percentage calculation results in a recurring decimal?
- A: Round the decimal to an appropriate number of decimal places based on the context of the problem. For most applications, rounding to two decimal places is sufficient.
-
Q: Can all fractions be easily converted to percentages with a whole number?
- A: No, many fractions will result in percentages with recurring decimals. This is perfectly normal and doesn't indicate an error in the calculation.
-
Q: Are there any online tools or calculators that can help with fraction to percentage conversions?
- A: While this article focuses on manual calculation, numerous online tools and calculators are available to perform these conversions quickly and easily.
Conclusion: Mastering Percentage Conversions
Converting fractions like 4/6 to percentages is a fundamental mathematical skill with broad applications. Understanding the different methods, from simplifying the fraction to using direct division, empowers you to tackle such problems confidently. Remember that the core concept involves finding an equivalent fraction with a denominator of 100 or dividing the numerator by the denominator and multiplying by 100. By mastering these techniques, you'll enhance your mathematical abilities and confidently navigate various quantitative challenges in your personal and professional life. Practice regularly to solidify your understanding and build fluency in percentage calculations. The ability to effortlessly convert fractions to percentages is a valuable tool in many contexts, making it a worthwhile skill to master.
Latest Posts
Latest Posts
-
Formula For Dilute Sulfuric Acid
Sep 08, 2025
-
Circuit With Ammeter And Voltmeter
Sep 08, 2025
-
Most Common Surname In Scotland
Sep 08, 2025
-
Maps Of South East Asia
Sep 08, 2025
-
Notre Dame Cathedral Rose Window
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 4 6 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.