4 50 As A Percent
marihuanalabs
Sep 23, 2025 · 5 min read
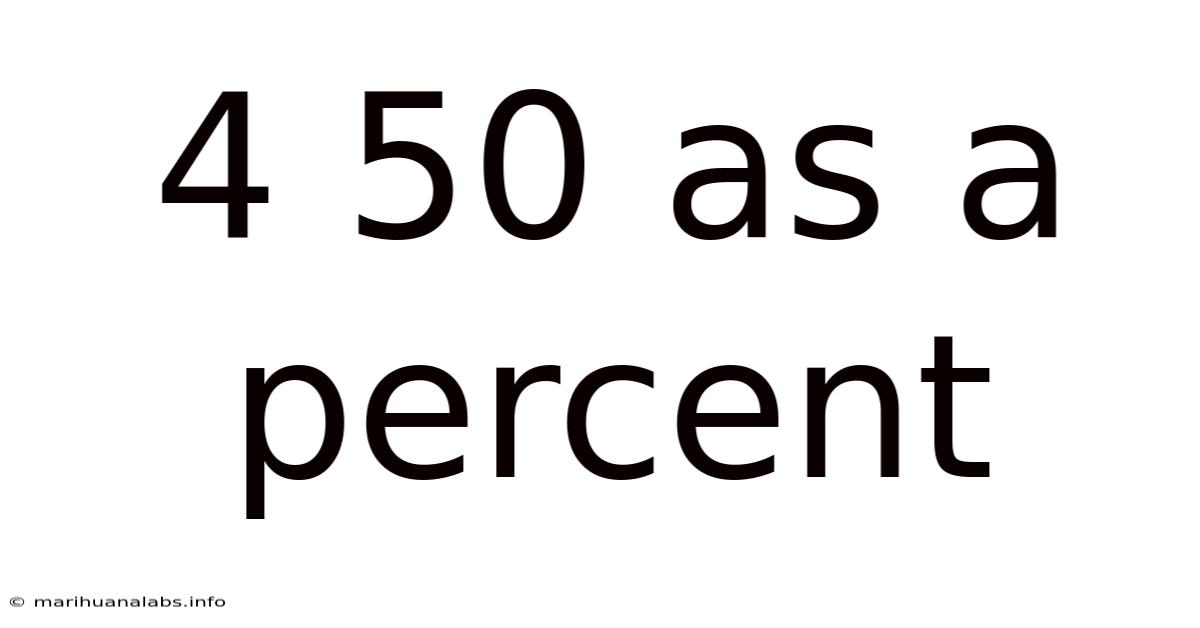
Table of Contents
4/50 as a Percent: A Comprehensive Guide to Understanding Fractions and Percentages
Understanding fractions and their conversion to percentages is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into the process of converting the fraction 4/50 into a percentage, explaining the underlying concepts and providing practical examples. We'll also explore related concepts and answer frequently asked questions to solidify your understanding. This guide aims to provide a thorough and approachable explanation, making the process clear even for those with limited mathematical backgrounds.
Introduction: Fractions and Percentages
A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, in the fraction 4/50, 4 is the numerator and 50 is the denominator. This means we have 4 parts out of a total of 50 parts.
A percentage, on the other hand, is a way of expressing a number as a fraction of 100. It's denoted by the symbol '%'. Percentages are widely used because they offer a standardized way to compare proportions and make calculations easier to understand. Converting fractions to percentages is a common task, often used in various fields like finance, statistics, and everyday calculations.
Converting 4/50 to a Percentage: Step-by-Step Guide
The conversion of a fraction to a percentage involves two main steps:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator. In this case:
4 ÷ 50 = 0.08
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.08 x 100 = 8%
Therefore, 4/50 is equal to 8%.
Simplifying the Fraction Before Conversion
While the above method is straightforward, we can simplify the process by first simplifying the fraction. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
The GCD of 4 and 50 is 2. Dividing both the numerator and the denominator by 2, we get:
4 ÷ 2 = 2 50 ÷ 2 = 25
So, the simplified fraction is 2/25. Now, we can repeat the two steps outlined above:
Step 1: Convert the simplified fraction to a decimal.
2 ÷ 25 = 0.08
Step 2: Convert the decimal to a percentage.
0.08 x 100 = 8%
As you can see, simplifying the fraction beforehand doesn't change the final result. It merely makes the division process simpler, especially when dealing with larger numbers.
Understanding the Concept: What does 8% mean?
8% means 8 parts out of 100. Imagine you have a pizza cut into 100 slices. 8% represents 8 of those slices. This standardized representation allows for easy comparisons. For example, if you have another fraction representing a different proportion, you can easily compare it to the 8% by converting it to a percentage as well.
Practical Applications of Percentage Conversions
Converting fractions to percentages is a crucial skill with diverse real-world applications:
-
Calculating Discounts: A store offers a 20% discount on an item. To calculate the discount amount, you'd convert the percentage to a fraction (20/100) and then multiply it by the original price.
-
Understanding Financial Statements: Financial reports often use percentages to represent various financial ratios and metrics, such as profit margins, debt-to-equity ratios, and return on investment (ROI). Understanding percentage conversions is key to interpreting these reports effectively.
-
Analyzing Statistical Data: Percentages are widely used in statistics to represent proportions and probabilities. Converting fractions to percentages makes it easier to understand and compare statistical data.
-
Calculating Grades: In many educational systems, grades are often represented as percentages. Understanding fraction-to-percentage conversion helps students understand their academic performance.
-
Everyday Calculations: Many everyday tasks, such as calculating tips, taxes, or splitting bills, involve percentage calculations. Mastering these conversions will simplify these calculations.
Further Exploration: Percentages Greater Than 100%
It's important to note that percentages can also be greater than 100%. This occurs when the numerator of the fraction is larger than the denominator. For example, if you have a fraction like 150/100, the equivalent percentage is 150%. This signifies that you have more than the whole amount. This situation often arises in contexts such as percentage increases or growth rates.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
A: Yes, you can convert any fraction to a percentage by following the steps described above. Even improper fractions (where the numerator is greater than the denominator) can be converted to percentages, resulting in percentages greater than 100%.
Q2: What if the fraction involves decimals?
A: If the fraction involves decimals, you can still convert it to a percentage using the same method. Simply divide the numerator by the denominator, and then multiply the resulting decimal by 100 to get the percentage.
Q3: Are there any alternative methods for converting fractions to percentages?
A: While the method of dividing the numerator by the denominator and then multiplying by 100 is the most common, you can also use proportional reasoning. For instance, you could set up a proportion: x/100 = 4/50. Solving for x will give you the percentage.
Q4: Why is it important to understand percentage conversions?
A: Understanding percentage conversions is crucial for navigating various aspects of everyday life and professional settings. It facilitates interpreting data, making informed decisions, and solving problems in diverse fields, from finance to education to everyday household tasks.
Conclusion: Mastering the Conversion of Fractions to Percentages
Converting fractions to percentages is a fundamental mathematical skill with broad real-world applications. By understanding the underlying concepts and following the straightforward steps outlined in this guide, you can confidently convert any fraction into its percentage equivalent. This skill is not just about solving mathematical problems; it's about enhancing your ability to interpret data, analyze information, and make informed decisions in numerous aspects of life. Remember to practice regularly, and you'll soon master this essential skill. From simplifying fractions to understanding the significance of percentages, this guide has provided a comprehensive pathway to achieving proficiency in this crucial area of mathematics.
Latest Posts
Latest Posts
-
Romeo And Juliet Themes Gcse
Sep 24, 2025
-
How To Figure Flow Rate
Sep 24, 2025
-
Screenplay For The Social Network
Sep 24, 2025
-
Cell Wall Vs Cell Membrane
Sep 24, 2025
-
Major Mountain System 5 Letters
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 4 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.