3x 2 2x 13 3
marihuanalabs
Sep 21, 2025 · 6 min read
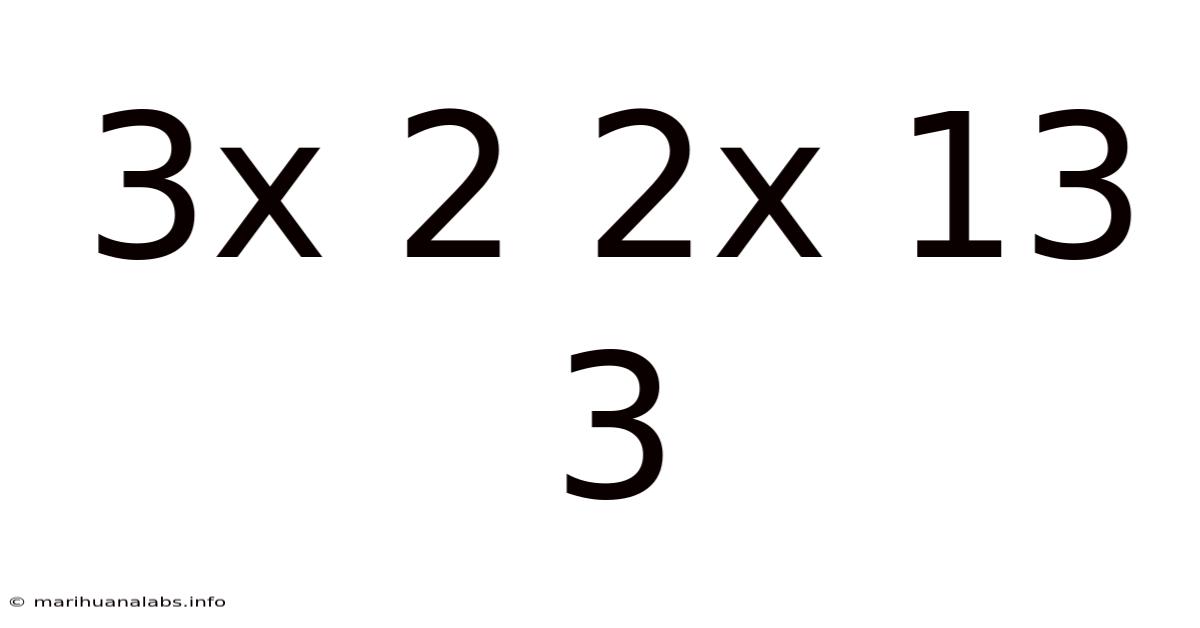
Table of Contents
Decoding the Sequence: Exploring the Mathematical Patterns in "3x 2, 2x 13, 3"
This article delves into the intriguing mathematical sequence "3x 2, 2x 13, 3," exploring its potential patterns and interpretations. While the sequence appears deceptively simple, a deeper analysis reveals a fascinating interplay of arithmetic operations and potentially hidden mathematical structures. We will explore various approaches to understanding this sequence, considering different perspectives and ultimately aiming to decipher its underlying logic. This exploration will benefit those interested in number theory, pattern recognition, and mathematical problem-solving.
Understanding the Given Sequence
The sequence "3x 2, 2x 13, 3" presents three distinct expressions, each involving multiplication. Let's break down each component:
- 3 x 2: This is a straightforward multiplication resulting in 6.
- 2 x 13: Similarly, this yields a product of 26.
- 3: This is a single digit, potentially representing a separate element or a consequence of a pattern.
The immediate challenge is to identify a unifying principle or a rule that connects these three seemingly disparate expressions. Are there any hidden mathematical relationships, or does the sequence simply represent a random collection of numbers?
Potential Interpretations and Patterns
Several approaches can be used to decipher the sequence’s underlying logic. Let's explore some possibilities:
1. Arithmetic Progressions and Series
One common approach in pattern recognition is to examine whether the results of the multiplications form an arithmetic progression or geometric progression.
-
Arithmetic Progression: An arithmetic progression is a sequence where the difference between consecutive terms is constant. In our case, the results are 6 and 26. The difference is 20. This is not immediately helpful without further information. However, we can explore if extending the pattern helps. Let's assume it is an arithmetic progression. The next element would be 26+20 = 46. But how would this relate to the solitary "3"?
-
Geometric Progression: A geometric progression is a sequence where the ratio between consecutive terms is constant. The ratio between 6 and 26 is approximately 4.33. This is not a whole number and doesn’t seem to provide a clear path. Again, the isolated "3" complicates this interpretation.
Therefore, simple arithmetic and geometric progressions don't appear to explain the full sequence.
2. Hidden Operations or Transformations
Perhaps the sequence involves more complex operations than simple multiplication. Let's consider some possibilities:
-
Alternating Operations: Could there be alternating operations between the expressions? For example, we could consider operations on the results (6 and 26). The difference between 26 and 6 is 20. The number 3, however, doesn't seem to fit into this simple subtraction pattern.
-
Modular Arithmetic: Modular arithmetic involves considering remainders after division. We could explore whether the remainders of the products (6 and 26) when divided by a particular number relate to the "3". While this is a possible line of investigation, it requires further exploration and testing with different moduli.
-
Prime Factorization: Examining the prime factorization of the numbers involved might unveil hidden relationships. The prime factorization of 6 is 2 x 3, and the prime factorization of 26 is 2 x 13. The presence of "3" in the factorization of 6 could be significant but requires further consideration within the context of the entire sequence.
3. Encoding or Symbolic Representation
It is possible that the sequence isn't purely numerical but represents some form of encoding or symbolic representation.
-
Base Conversion: Perhaps the numbers are represented in a different number base. However, without further context or clues, it is difficult to determine which base to use.
-
Cipher or Code: It's plausible that the sequence is part of a more extensive cipher or code, requiring a key or further information to decipher.
Expanding the Possibilities: Considering Context
To gain a deeper understanding, we need to consider the context in which this sequence was presented. Where did you encounter this sequence? The source might hold important clues. Was it part of a larger problem, a puzzle, or a code? Knowing the context will significantly aid in interpreting its meaning.
For example:
-
A Puzzle: If this sequence was presented as a puzzle, the solution might involve finding a rule that connects all three elements, generating a new term or solving a related problem.
-
A Code: If it's a code, the "3" might be a delimiter, a checksum, or part of a key to decrypt further information.
-
A Mathematical Problem: The sequence could be part of a larger mathematical problem that requires the identification of a recursive relation, function, or pattern to solve.
Advanced Mathematical Techniques
If the simpler approaches fail, we may need to consider more advanced mathematical techniques:
-
Recurrence Relations: These are equations that define a sequence based on its previous terms. We could explore if a recurrence relation can generate the sequence "6, 26, 3".
-
Generating Functions: These are power series whose coefficients represent the terms of a sequence. They can be used to find closed-form expressions for sequences.
-
Discrete Mathematics: Concepts from discrete mathematics, like graph theory or combinatorial analysis, might be relevant if the sequence represents a combinatorial problem or a structure that can be represented graphically.
The Importance of Context and Further Investigation
The ambiguity of the sequence "3x 2, 2x 13, 3" highlights the crucial role of context in mathematical problem-solving. Without additional information or context, it is impossible to definitively determine the underlying pattern or meaning. The analysis presented here explores various approaches to interpreting such sequences, emphasizing the need for a systematic investigation and the importance of considering different possibilities, including those outside purely numerical interpretations. More information about the origin or purpose of this sequence is crucial for a complete and accurate analysis.
Frequently Asked Questions (FAQ)
Q: Is there a single definitive answer to the meaning of this sequence?
A: No. Without additional context, there is no single, definitive answer. Multiple interpretations are possible.
Q: Could this be a random sequence?
A: It's possible, although less likely if it's part of a problem or puzzle. The appearance of structured mathematical expressions suggests a potential underlying pattern, even if it's complex or hidden.
Q: What are some key steps to solving similar number sequences?
A:
- Analyze the given numbers: Look for patterns, common factors, differences, and ratios.
- Consider different mathematical operations: Explore addition, subtraction, multiplication, division, modulo operations, and more complex combinations.
- Investigate number properties: Examine prime factorization, divisibility rules, and other number-theoretic properties.
- Check for arithmetic or geometric progressions: See if the terms form a simple sequence.
- Look for hidden patterns: Consider alternating operations, transformations, or encodings.
- Explore advanced techniques: If basic methods fail, consider recurrence relations, generating functions, or other advanced techniques.
- Consider the context: The source of the sequence provides valuable clues.
Conclusion
The sequence "3x 2, 2x 13, 3" presents a compelling challenge in mathematical pattern recognition. While a definitive solution remains elusive without further context, exploring various approaches, from simple arithmetic to more advanced techniques, allows us to develop a deeper appreciation for the complexities and nuances of mathematical problem-solving. The lack of a singular answer underscores the importance of critical thinking, creativity, and the open-minded exploration of different mathematical concepts when deciphering numerical sequences. Further investigation, particularly with the addition of context, is needed to unlock the true meaning of this fascinating sequence.
Latest Posts
Latest Posts
-
Nathan Jones By The Supremes
Sep 21, 2025
-
Is Sea A Collective Noun
Sep 21, 2025
-
Mammals Amphibians Reptiles Birds Fish
Sep 21, 2025
-
What Is 55f In Celsius
Sep 21, 2025
-
Fiction Is Fake Or Real
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 2x 13 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.