32 40 As A Percentage
marihuanalabs
Sep 16, 2025 · 5 min read
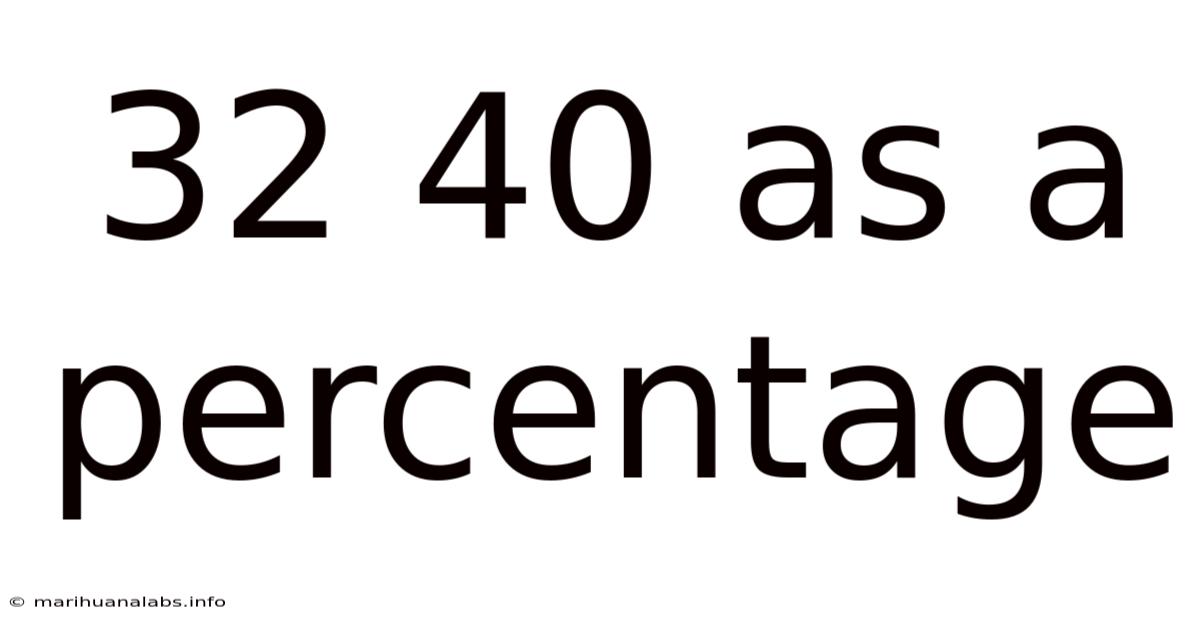
Table of Contents
Understanding 32 out of 40 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial analysis. This article provides a thorough explanation of how to determine the percentage equivalent of 32 out of 40, along with various methods, practical applications, and a deeper dive into the underlying mathematical concepts. Understanding this seemingly simple calculation opens doors to a broader comprehension of proportional reasoning and its widespread utility.
Introduction: Why Percentages Matter
Percentages express a proportion or ratio as a fraction of 100. They offer a standardized way to compare different quantities and are crucial for interpreting data, making informed decisions, and communicating information clearly. Knowing how to calculate percentages, particularly in scenarios like 32 out of 40, is essential for students, professionals, and anyone navigating the quantitative aspects of everyday life. This article will demystify this calculation, exploring multiple approaches and highlighting the underlying principles.
Method 1: The Fraction Method
The most intuitive approach to calculating 32 out of 40 as a percentage involves representing the given values as a fraction and then converting it to a percentage.
-
Express as a Fraction: The problem "32 out of 40" translates directly into the fraction 32/40.
-
Simplify the Fraction (Optional): While not strictly necessary, simplifying the fraction makes the subsequent calculations easier. Both 32 and 40 are divisible by 8: 32/40 simplifies to 4/5.
-
Convert to Decimal: To change a fraction to a percentage, first convert it to a decimal by dividing the numerator (top number) by the denominator (bottom number): 4 ÷ 5 = 0.8
-
Convert Decimal to Percentage: Multiply the decimal by 100 and add the "%" symbol: 0.8 x 100 = 80%.
Therefore, 32 out of 40 is 80%.
Method 2: Using Proportions
This method leverages the concept of proportions to solve for the unknown percentage.
-
Set up a Proportion: We can represent the problem as a proportion: 32/40 = x/100, where 'x' represents the percentage we want to find.
-
Cross-Multiply: Cross-multiply the terms: 32 * 100 = 40 * x, which simplifies to 3200 = 40x.
-
Solve for x: Divide both sides of the equation by 40 to isolate 'x': x = 3200 ÷ 40 = 80.
Therefore, x = 80, meaning 32 out of 40 is 80%.
Method 3: Using a Calculator
Modern calculators significantly simplify percentage calculations.
-
Enter the Fraction: Input 32 ÷ 40 into your calculator.
-
Convert to Percentage: Most calculators have a percentage function (often represented by a "%" symbol). Press this button to directly convert the decimal result to a percentage. Alternatively, multiply the decimal result by 100.
This method offers a quick and efficient way to find the percentage.
Understanding the Mathematical Concept: Ratios and Proportions
The calculation of 32 out of 40 as a percentage fundamentally relies on understanding ratios and proportions.
A ratio is a comparison of two or more quantities. In this case, the ratio is 32:40, indicating the relationship between the number of successful attempts (32) and the total number of attempts (40).
A proportion is a statement of equality between two ratios. We use proportions to solve for unknown values, as demonstrated in Method 2. The ability to manipulate ratios and proportions is vital for various mathematical applications, including solving percentage problems, scaling recipes, and understanding financial ratios.
Practical Applications of Percentage Calculations
The ability to calculate percentages like 32 out of 40 has broad practical applications:
-
Academic Performance: Calculating grades, test scores, and overall academic performance frequently involves percentages. A score of 32 out of 40 on a test translates to an 80%, providing a clear understanding of performance.
-
Financial Calculations: Percentages are fundamental in finance for calculating interest rates, discounts, tax rates, profit margins, and investment returns.
-
Data Analysis: Percentages are used extensively in data analysis and statistics to represent proportions, trends, and changes in data.
-
Everyday Life: Percentages are used in everyday situations such as calculating sales tax, tips in restaurants, and understanding discounts in stores.
Beyond the Basics: Working with Percentages in More Complex Scenarios
While the example of 32 out of 40 is relatively straightforward, the underlying principles extend to more complex percentage calculations. Consider these scenarios:
-
Calculating Percentage Increase or Decrease: Determining the percentage change between two values requires understanding how to calculate the difference, express it as a fraction of the original value, and then convert to a percentage.
-
Working with Percentages of Percentages: In some scenarios, you might need to calculate a percentage of another percentage. For example, finding 20% of 80% would involve multiplying the two percentages (0.20 x 0.80 = 0.16 or 16%).
-
Applying Percentages to Compound Interest: Compound interest calculations involve applying percentages repeatedly over time, leading to exponential growth (or decay).
Frequently Asked Questions (FAQ)
Q: What if the numbers weren't as easily divisible?
A: If the numbers are not easily simplified, you can still use the fraction method or the proportion method. A calculator will be particularly useful in these cases to handle the decimal calculations.
Q: Is there a formula for calculating percentages?
A: The basic formula is: (Part / Whole) x 100 = Percentage. The 'part' is the value you're expressing as a percentage of the 'whole'.
Q: Can I use a spreadsheet program to calculate percentages?
A: Yes, spreadsheet programs like Microsoft Excel or Google Sheets have built-in functions for calculating percentages, making the process very efficient, especially for large datasets.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate percentages, specifically in examples like 32 out of 40, is a vital skill for success in various aspects of life. Whether you use the fraction method, the proportion method, or a calculator, the key lies in understanding the underlying mathematical concepts of ratios and proportions. Mastering these principles allows you to tackle more complex percentage calculations and apply this fundamental skill effectively in diverse situations. Remember that practice is key to solidifying your understanding and developing proficiency in calculating percentages. The ability to quickly and accurately determine percentages empowers you to interpret data, make informed decisions, and communicate quantitative information clearly and concisely.
Latest Posts
Latest Posts
-
Tiny Bugs In Houseplant Soil
Sep 16, 2025
-
A Net Of A Cone
Sep 16, 2025
-
Calculate Resistor For Voltage Drop
Sep 16, 2025
-
St Martin Church Cologne Germany
Sep 16, 2025
-
Indigenous Tribes In New Zealand
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 32 40 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.