3 50 As A Percent
marihuanalabs
Sep 12, 2025 · 5 min read
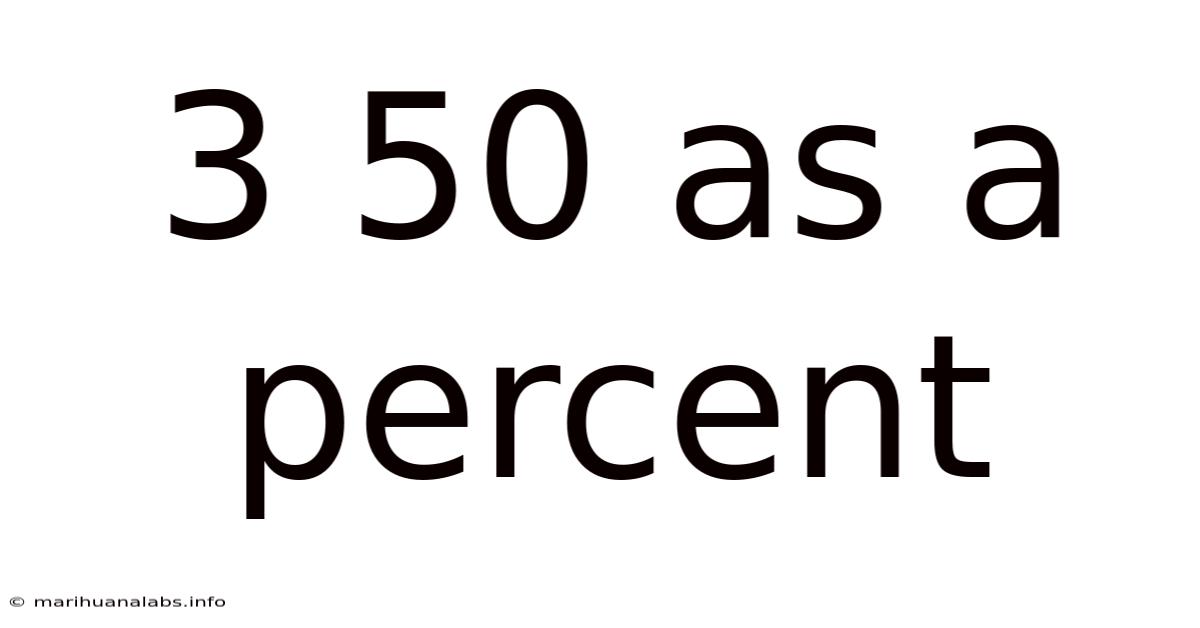
Table of Contents
3/50 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax rates to understanding statistical data and financial reports. This comprehensive guide will delve into the process of converting the fraction 3/50 into a percentage, explaining the underlying principles and providing multiple approaches to solve this type of problem. We'll also explore common mistakes and offer practical examples to solidify your understanding. This guide aims to be your go-to resource for mastering fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before diving into the conversion, let's refresh our understanding of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 3/50, 3 represents the part and 50 represents the whole.
A percentage, denoted by the symbol %, represents a fraction of 100. It essentially expresses a proportion relative to 100. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100, or 1/2.
Method 1: Converting the Fraction Directly
The most straightforward method to convert 3/50 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (50). 3 ÷ 50 = 0.06
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the percentage symbol (%). 0.06 × 100 = 6%
Therefore, 3/50 is equal to 6%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another approach involves creating an equivalent fraction with a denominator of 100. This method is particularly useful when the denominator is a factor of 100 or can be easily manipulated to become one.
To achieve this:
-
Determine the factor: We need to find what number, when multiplied by 50, equals 100. This number is 2 (50 x 2 = 100).
-
Multiply both the numerator and the denominator by the factor: Multiply both the numerator and the denominator of 3/50 by 2: (3 x 2) / (50 x 2) = 6/100
-
Convert the equivalent fraction to a percentage: Since the denominator is now 100, the numerator directly represents the percentage. Therefore, 6/100 is equal to 6%.
This method clearly demonstrates the relationship between fractions and percentages, highlighting that a percentage is simply a fraction with a denominator of 100.
Method 3: Using Proportions
The concept of proportions provides a more formal mathematical approach to solving this problem. We can set up a proportion to solve for the unknown percentage:
3/50 = x/100
To solve for x (the percentage), we cross-multiply:
50x = 300
Divide both sides by 50:
x = 6
Therefore, 3/50 is equal to 6%. This method reinforces the fundamental principles of proportionality and equivalence in mathematics.
Understanding the Significance of 6%
The result of 6% provides valuable context depending on the application. For example:
- In a test: If a student answered 3 out of 50 questions correctly, their score is 6%.
- In sales: A 6% discount on a product represents a reduction of 6 cents for every dollar.
- In finance: A 6% interest rate means earning 6 units of currency for every 100 units invested.
Common Mistakes to Avoid
While the conversion of 3/50 to a percentage seems straightforward, some common mistakes can occur:
- Incorrect decimal placement: Carefully divide the numerator by the denominator to ensure the decimal point is correctly placed. A misplaced decimal can significantly alter the final percentage.
- Forgetting to multiply by 100: Remember that converting a decimal to a percentage requires multiplying by 100. Simply writing the decimal as a percentage without this step leads to an inaccurate result.
- Incorrect simplification: When using equivalent fractions, ensure the numerator and denominator are multiplied by the same factor. Using different factors will result in an incorrect equivalent fraction.
Expanding on the Concept: Working with More Complex Fractions
The methods described above can be applied to convert any fraction to a percentage. Let's consider some examples:
- 15/25: First, convert 15/25 to a decimal (15 ÷ 25 = 0.6). Then, multiply by 100 (0.6 x 100 = 60%). Therefore, 15/25 = 60%.
- 7/8: Convert 7/8 to a decimal (7 ÷ 8 = 0.875). Multiply by 100 (0.875 x 100 = 87.5%). Therefore, 7/8 = 87.5%.
- 1/3: This fraction results in a repeating decimal (1 ÷ 3 = 0.333...). Multiplying by 100 gives approximately 33.33%. It's important to note that some fractions will produce non-terminating decimals, requiring rounding for practical applications.
Frequently Asked Questions (FAQ)
-
Can I use a calculator for this conversion? Absolutely! Calculators can simplify the decimal conversion process, especially for more complex fractions.
-
What if the fraction is an improper fraction (numerator is greater than the denominator)? The process remains the same. Convert the improper fraction to a decimal, and then multiply by 100. The resulting percentage will be greater than 100%.
-
What if the fraction has a large denominator? Using a calculator is highly recommended for fractions with large denominators to avoid manual calculation errors.
Conclusion
Converting the fraction 3/50 to a percentage is a fundamental mathematical operation with numerous practical applications. Whether you use the direct method, the equivalent fraction method, or the proportion method, the result remains consistent: 3/50 equals 6%. Understanding the underlying principles and practicing these methods will empower you to confidently handle fraction-to-percentage conversions in various contexts, enhancing your mathematical skills and problem-solving abilities. Remember to practice regularly and utilize the most efficient method that suits your understanding and the complexity of the problem at hand. Mastering this skill will significantly contribute to your mathematical proficiency and ability to interpret numerical data effectively.
Latest Posts
Latest Posts
-
Where Is The Radleys Filmed
Sep 12, 2025
-
Lawrence Of Arabia Book Author
Sep 12, 2025
-
Revolt Of The Northern Earls
Sep 12, 2025
-
The Age Of Reason Sartre
Sep 12, 2025
-
1 2 Litre In Ml
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.