3 15 As A Percent
marihuanalabs
Sep 14, 2025 · 5 min read
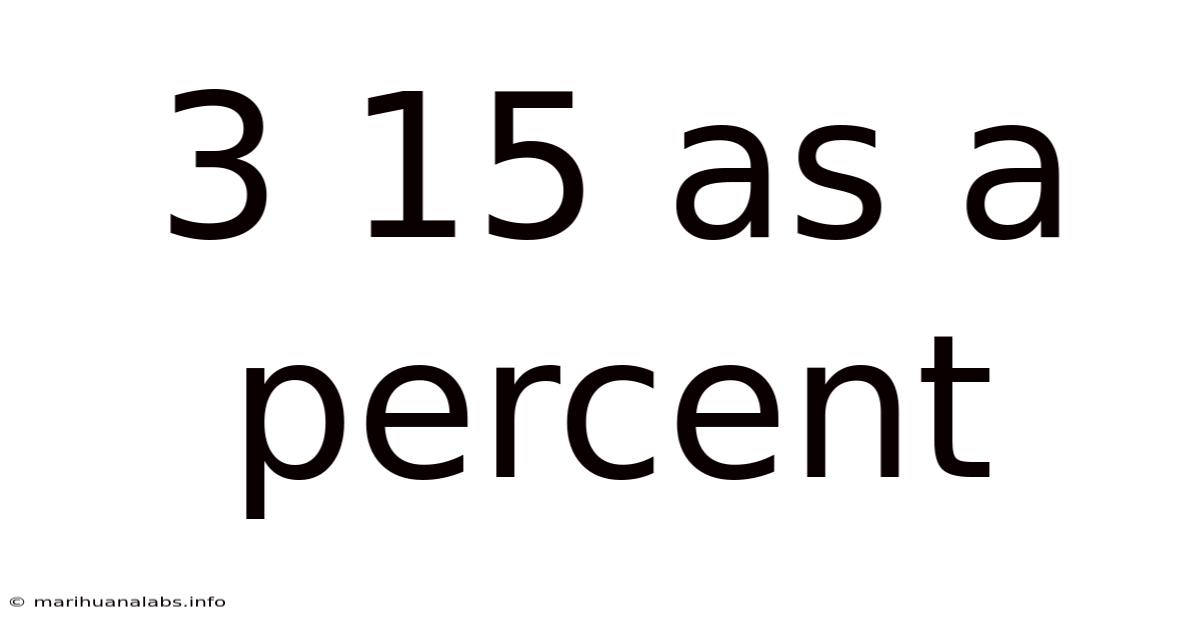
Table of Contents
Understanding 3/15 as a Percentage: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in various fields, from finance and statistics to everyday calculations. This comprehensive guide will delve deep into understanding how to convert the fraction 3/15 into a percentage, explaining the process step-by-step and exploring related concepts. We'll cover the underlying principles, provide practical examples, and answer frequently asked questions to ensure a thorough grasp of the topic.
Introduction: Fractions, Decimals, and Percentages
Before diving into the specifics of 3/15, let's review the fundamental relationship between fractions, decimals, and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator and denominator). A decimal is a way of expressing a number using a base-ten system, where a decimal point separates the whole number part from the fractional part. A percentage is a way of expressing a fraction or decimal as a proportion of 100, indicated by the symbol %.
These three forms are interchangeable. We can convert a fraction to a decimal by dividing the numerator by the denominator. We can then convert this decimal to a percentage by multiplying it by 100 and adding the "%" symbol. Conversely, we can convert a percentage to a decimal by dividing it by 100, and then convert that decimal to a fraction.
Step-by-Step Conversion of 3/15 to a Percentage
Now, let's focus on converting the fraction 3/15 to a percentage. We'll follow these simple steps:
Step 1: Simplify the Fraction
The first step involves simplifying the fraction 3/15. This means finding the greatest common divisor (GCD) of the numerator (3) and the denominator (15). The GCD of 3 and 15 is 3. Dividing both the numerator and the denominator by the GCD, we get:
3 ÷ 3 = 1 15 ÷ 3 = 5
Therefore, the simplified fraction is 1/5. Simplifying the fraction makes the subsequent calculations easier.
Step 2: Convert the Fraction to a Decimal
To convert the simplified fraction 1/5 to a decimal, we divide the numerator (1) by the denominator (5):
1 ÷ 5 = 0.2
So, the decimal equivalent of 1/5 is 0.2.
Step 3: Convert the Decimal to a Percentage
Finally, to convert the decimal 0.2 to a percentage, we multiply it by 100 and add the "%" symbol:
0.2 × 100 = 20
Therefore, 3/15 is equal to 20%.
Alternative Method: Direct Conversion
While the above method is preferred for clarity and understanding, you can also directly convert 3/15 to a percentage without simplifying first. You would simply divide 3 by 15 and then multiply by 100:
3 ÷ 15 = 0.2 0.2 × 100 = 20%
Both methods yield the same result: 20%.
Understanding the Result: What Does 20% Mean?
The result, 20%, signifies that 3 is 20% of 15. This means that if you divide 15 into 100 equal parts, 3 would represent 20 of those parts. This percentage representation is useful for comparing proportions, understanding ratios, and performing calculations involving parts of a whole.
Practical Applications of Percentage Conversions
The ability to convert fractions to percentages has numerous practical applications:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates.
- Statistics: Representing data as proportions, interpreting survey results, and analyzing probabilities.
- Science: Expressing concentrations, experimental yields, and error margins.
- Everyday Life: Calculating tips, sales tax, and understanding discounts in shopping.
Further Exploration: Working with Percentages
Once you understand the basics of percentage conversion, you can explore more advanced concepts:
- Percentage Increase/Decrease: Calculating the percentage change between two values.
- Finding a Percentage of a Number: Determining a specific portion of a given number.
- Reverse Percentage Calculations: Finding the original value when given a percentage and the resulting value.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying the fraction important?
Simplifying the fraction makes the calculation easier and reduces the risk of errors. Working with smaller numbers is generally simpler and less prone to mistakes.
Q2: Can I convert any fraction to a percentage?
Yes, you can convert any fraction to a percentage by following the steps outlined above. However, fractions with very large denominators may result in decimals with many digits after the decimal point.
Q3: What if the decimal has more than two digits after the decimal point?
If the decimal has more than two digits after the decimal point when converting a fraction to a percentage, you can round the number to two decimal places for practical purposes. For example, 0.2345 can be rounded to 0.23, representing 23%.
Q4: Are there online calculators to help with percentage conversions?
Yes, many online calculators are available to assist with fraction-to-percentage conversions. These tools can be helpful for quick calculations, especially when dealing with complex fractions. However, understanding the underlying principles remains crucial.
Conclusion: Mastering Percentage Conversions
Converting fractions like 3/15 to percentages is a fundamental skill with widespread applications. By understanding the steps involved – simplifying the fraction, converting to a decimal, and then to a percentage – you can confidently tackle various percentage-related problems. Remember that the key to mastery lies not just in memorizing the steps, but in understanding the underlying relationships between fractions, decimals, and percentages. This understanding empowers you to solve real-world problems involving proportions, ratios, and comparative analysis across diverse fields. The ability to easily convert between these forms is a valuable asset in many aspects of life and learning. Practice regularly, and you will become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
Greek God Tattoos For Men
Sep 14, 2025
-
M E A T Meet
Sep 14, 2025
-
What Is Uncertainty In Physics
Sep 14, 2025
-
Formula For Pressure In Liquids
Sep 14, 2025
-
Why Are Ionic Substances Brittle
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 3 15 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.