3 10 As A Percent
marihuanalabs
Sep 20, 2025 · 5 min read
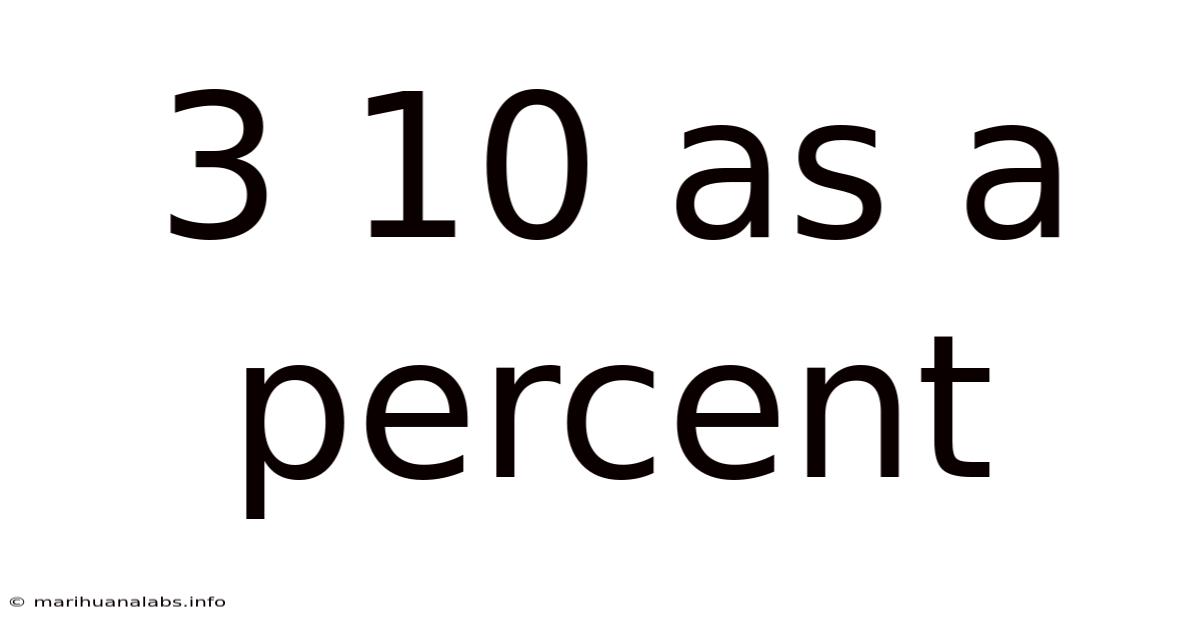
Table of Contents
3/10 as a Percent: A Comprehensive Guide to Understanding Fractions and Percentages
Understanding fractions and percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide will delve into how to express the fraction 3/10 as a percentage, explaining the underlying concepts and providing practical examples. We'll explore various methods to convert fractions to percentages and address common questions surrounding this topic. By the end, you'll not only know that 3/10 is equivalent to 30%, but you'll also grasp the broader principles involved in fraction-to-percentage conversions.
Understanding Fractions and Percentages
Before we dive into converting 3/10 to a percentage, let's briefly review the basics of fractions and percentages.
A fraction represents a part of a whole. It's composed of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator shows the total number of equal parts the whole is divided into. For example, in the fraction 3/10, 3 is the numerator and 10 is the denominator. This means we have 3 parts out of a total of 10 equal parts.
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Percentages are often denoted by the symbol "%". For instance, 50% means 50 out of 100, or 50/100.
The relationship between fractions and percentages is crucial. A percentage is simply a fraction with a denominator of 100. Converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100, then expressing the numerator as a percentage.
Method 1: Direct Conversion (Denominator of 10)
The simplest method for converting 3/10 to a percentage leverages the fact that the denominator is already a factor of 100.
To convert a fraction to a percentage, we can use the following formula:
(Numerator / Denominator) * 100%
In the case of 3/10:
(3 / 10) * 100% = 30%
Therefore, 3/10 is equal to 30%. This method is particularly straightforward when the denominator is a factor of 100 (such as 10, 20, 25, 50).
Method 2: Decimal Conversion
Another common method involves first converting the fraction to a decimal and then multiplying by 100%.
-
Convert the fraction to a decimal: Divide the numerator (3) by the denominator (10): 3 ÷ 10 = 0.3
-
Multiply the decimal by 100%: 0.3 * 100% = 30%
Again, we arrive at the answer: 3/10 is equal to 30%. This method is versatile and can be used for fractions with any denominator.
Method 3: Proportion Method
This method is useful for understanding the underlying principle of percentage calculations. It relies on setting up a proportion:
- Fraction: 3/10
- Percentage: x/100 (where 'x' represents the percentage we want to find)
We set up the proportion:
3/10 = x/100
To solve for 'x', we cross-multiply:
10x = 300
Divide both sides by 10:
x = 30
Therefore, x = 30%, confirming that 3/10 is equal to 30%.
Visual Representation
Understanding percentages can be enhanced through visual aids. Imagine a rectangle divided into 10 equal parts. If you shade 3 of those parts, you've shaded 3/10 of the rectangle. Since 10 parts make up the whole (100%), each part represents 10% (100%/10 = 10%). Therefore, shading 3 parts represents 3 * 10% = 30%. This visual method provides an intuitive understanding of the conversion.
Real-world Applications
The ability to convert fractions to percentages is incredibly useful in many real-world scenarios:
-
Discounts: A store offering a 3/10 discount on an item is offering a 30% discount.
-
Grades: If you answered 3 out of 10 questions correctly on a test, you scored 30%.
-
Statistics: Representing data in percentages often makes it easier to understand and compare. For example, if 3 out of 10 people prefer a certain product, 30% prefer it.
-
Finance: Understanding interest rates, tax calculations, and profit margins often involves working with percentages.
Common Mistakes to Avoid
While the conversion of 3/10 to a percentage is relatively straightforward, some common mistakes can occur when working with more complex fractions:
-
Incorrect Order of Operations: Always perform the division before multiplying by 100%.
-
Forgetting the Percentage Sign: Remember to include the "%" symbol to indicate that your answer is a percentage.
-
Rounding Errors: When dealing with decimals that don't terminate neatly, pay attention to the required level of accuracy.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a percentage?
- A: Yes, absolutely. Any fraction can be converted to a percentage using the methods described above.
-
Q: What if the denominator is not a factor of 100?
- A: You can still use the decimal conversion method or the proportion method.
-
Q: How do I convert a percentage back to a fraction?
- A: To convert a percentage back to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 30% becomes 30/100, which simplifies to 3/10.
-
Q: What if I have a mixed number (e.g., 1 3/10)?
- A: First convert the mixed number to an improper fraction (in this case, 13/10), then use any of the methods outlined to convert it to a percentage. (13/10 * 100% = 130%).
Conclusion
Converting 3/10 to a percentage is a fundamental mathematical operation with broad practical applications. We've explored three different methods for performing this conversion, highlighting their advantages and demonstrating their use. By understanding these methods and the underlying concepts of fractions and percentages, you'll be well-equipped to tackle a wide range of percentage-related problems. Remember to practice regularly to build confidence and fluency in these essential mathematical skills. Mastering these conversions will enhance your problem-solving capabilities across various disciplines and everyday scenarios. The seemingly simple task of understanding 3/10 as 30% opens doors to a deeper understanding of numerical representation and its practical applications in the world around us.
Latest Posts
Latest Posts
-
Alcl4 Dot And Cross Diagram
Sep 20, 2025
-
Animal Farm Chapter 4 Summary
Sep 20, 2025
-
Difference Of Lake And River
Sep 20, 2025
-
Map Of The Northern Hemisphere
Sep 20, 2025
-
Well Known Places In Brazil
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 3 10 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.