2x X 2 X 2
marihuanalabs
Sep 12, 2025 · 5 min read
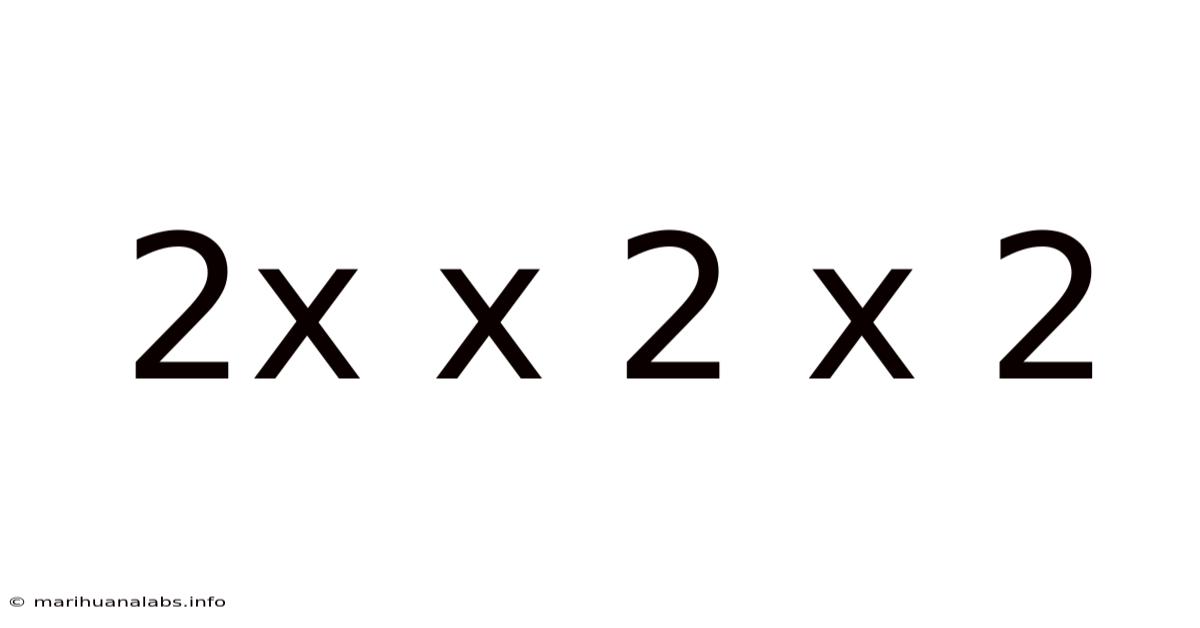
Table of Contents
Exploring the Mathematical and Conceptual Depths of 2 x 2 x 2: Beyond Simple Multiplication
The seemingly simple equation, 2 x 2 x 2, offers a surprising depth of exploration. While a child might quickly calculate the answer as 8, delving deeper reveals connections to various mathematical concepts, real-world applications, and even philosophical implications. This article will explore this seemingly simple equation from multiple perspectives, showcasing its surprising versatility and significance.
I. The Fundamentals: Multiplication and Exponents
At its core, 2 x 2 x 2 is a multiplication problem. Multiplication, a fundamental arithmetic operation, represents repeated addition. In this case, we are adding two groups of two, twice. This can be visually represented using several methods, from simple arrays of dots to more abstract models.
-
Visual Representation: Imagine two rows of two dots each. This represents 2 x 2 = 4. Now, imagine stacking another identical layer of two rows and two columns of dots on top. This represents 4 x 2 = 8, effectively showing the calculation of 2 x 2 x 2.
-
Repeated Addition: Alternatively, we can view it as 2 + 2 + 2 + 2 = 8. We are adding the number 2 to itself four times.
Beyond simple multiplication, this equation introduces the concept of exponents. 2 x 2 x 2 can be more concisely written as 2³. Here, the '3' is the exponent, indicating that the base number (2) is multiplied by itself three times. Understanding exponents is crucial for more advanced mathematical concepts such as algebra, calculus, and even computer science.
II. Exploring Binary Systems and Computer Science
The number 2 plays a critical role in binary systems, the foundation of modern computing. Binary uses only two digits, 0 and 1, to represent all numbers. This system is directly related to the equation 2 x 2 x 2.
-
Binary Representation: The number 8, the result of 2 x 2 x 2, is represented as 1000 in binary. This representation highlights the significance of powers of 2 in the binary system. Each position represents a power of 2: 2³, 2², 2¹, and 2⁰ (or 1).
-
Data Storage: Computers store data using bits, which are binary digits (0 or 1). Bytes, units of computer data, typically consist of 8 bits. This connection to 2 x 2 x 2 underscores the fundamental role of powers of two in shaping the architecture of computer systems and how data is organized and manipulated.
-
Memory Addressing: Memory addresses in computer systems are often based on powers of 2, allowing efficient access to data. The power of two structure directly reflects the underlying binary system.
III. Geometric Interpretations: Cubes and Volume
Geometrically, 2 x 2 x 2 can represent the volume of a cube. Imagine a cube with sides of length 2 units. The volume of this cube is calculated as length x width x height, which equals 2 x 2 x 2 = 8 cubic units. This connection demonstrates the practical application of this equation in geometry and spatial reasoning.
-
Extending to Higher Dimensions: The concept can be extended to higher dimensions. While 2 x 2 x 2 represents the volume of a three-dimensional cube, 2 x 2 represents the area of a square, and 2 itself represents the length of a line segment. This provides a visual and conceptual bridge between different dimensions.
-
Practical Applications: This geometrical interpretation has broad applications, ranging from calculating the volume of containers to designing three-dimensional structures in architecture and engineering.
IV. The Power of Two: Growth and Exponential Functions
The equation 2 x 2 x 2 demonstrates the principle of exponential growth. Exponential growth occurs when a quantity increases at a rate proportional to its current value. This is evident in the rapid increase in the result as we continue to multiply by 2.
-
Real-World Examples: Many phenomena in nature and society exhibit exponential growth, such as population growth under ideal conditions, the spread of diseases, and the compounding of interest in finance. Understanding exponential growth is crucial for modeling and predicting these types of changes.
-
Exponential Functions: The equation 2 x 2 x 2 is a simple example of an exponential function, which can be generalized as aⁿ, where 'a' is the base and 'n' is the exponent. These functions play a fundamental role in various scientific and engineering fields.
V. Beyond the Numbers: Philosophical and Conceptual Implications
While primarily a mathematical equation, 2 x 2 x 2 invites us to consider broader conceptual questions.
-
Simplicity and Complexity: The equation's simplicity belies its multifaceted nature. It showcases how simple concepts can lead to intricate and far-reaching implications.
-
Abstraction and Representation: The equation serves as an abstract representation of various real-world phenomena. This highlights the power of mathematics to model and understand complex systems.
-
Building Blocks of Knowledge: The equation exemplifies the fundamental building blocks of mathematics and how seemingly simple components combine to create more complex structures and understanding.
VI. Frequently Asked Questions (FAQs)
-
Q: What is the answer to 2 x 2 x 2?
- A: The answer is 8.
-
Q: What is the exponential form of 2 x 2 x 2?
- A: 2³ (2 cubed).
-
Q: How is 2 x 2 x 2 related to binary code?
- A: The number 8 (the result of 2 x 2 x 2) is represented as 1000 in binary, highlighting the importance of powers of 2 in computer systems.
-
Q: Are there any real-world applications of 2 x 2 x 2 beyond calculating volume?
- A: Yes, the concept of exponential growth, represented by repeated multiplication, applies to many real-world scenarios, including population growth and compound interest.
-
Q: How does 2 x 2 x 2 relate to other mathematical concepts?
- A: It connects to concepts like exponents, powers of two, binary systems, geometric volume calculations, and exponential functions.
VII. Conclusion:
The seemingly straightforward calculation of 2 x 2 x 2 reveals a surprising depth of mathematical concepts and real-world applications. From the fundamentals of multiplication and exponents to the intricacies of binary systems and exponential growth, this equation serves as a gateway to understanding more complex mathematical and scientific principles. Its simplicity belies its power, illustrating how fundamental concepts form the basis for more advanced knowledge and applications across numerous fields. It's a reminder that even the simplest mathematical expressions can hold profound implications and open doors to a deeper understanding of the world around us. The journey from a simple calculation to the wider implications of exponential growth, binary systems, and geometric representation showcases the beauty and power of mathematical exploration.
Latest Posts
Latest Posts
-
What Does Sm And Cr Stand For
Sep 12, 2025
-
1 69 M Height In Feet
Sep 12, 2025
-
Rf Values Of Amino Acids
Sep 12, 2025
-
Spend Mark Zuckerberg Money Nealfun Org
Sep 12, 2025
-
How To Plan A Book
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 2x X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.