2 5 Divided By 2
marihuanalabs
Sep 07, 2025 · 5 min read
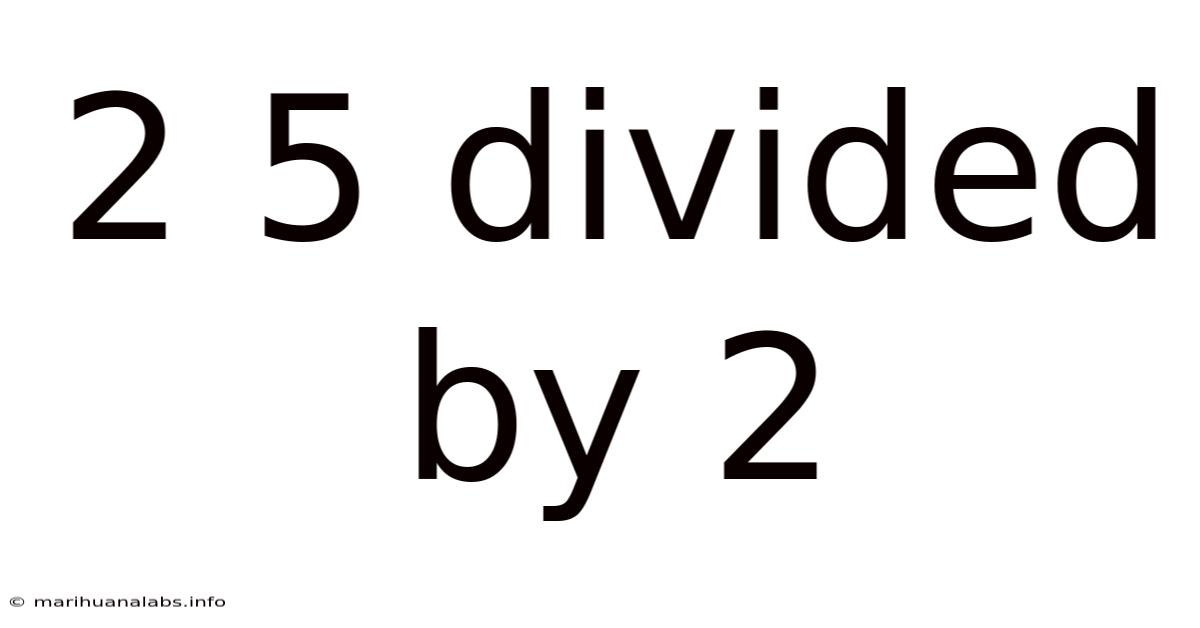
Table of Contents
Decoding 25 Divided by 2: A Deep Dive into Division and its Applications
Understanding division is a fundamental skill in mathematics, crucial for navigating everyday life and tackling more complex mathematical concepts. This article explores the seemingly simple calculation of 25 divided by 2, delving into various approaches, interpretations, and its relevance across diverse fields. We'll move beyond the basic answer to uncover the deeper mathematical principles and practical applications of this seemingly straightforward operation. This will help you develop a stronger understanding of division, fractions, decimals, and their importance in problem-solving.
Understanding the Problem: 25 ÷ 2
At its core, the problem "25 divided by 2" asks: how many times does 2 fit into 25? This question leads us to several ways to solve the problem and understand the result.
Method 1: Long Division
The traditional method is long division. This method systematically breaks down the division process, providing a clear step-by-step approach.
-
Set up the problem: Write 25 inside the long division bracket ( ) and 2 outside.
-
Divide: How many times does 2 go into 2? The answer is 1. Write 1 above the 2 in 25.
-
Multiply: Multiply the quotient (1) by the divisor (2). This gives 2. Write 2 below the 2 in 25.
-
Subtract: Subtract 2 from 2. This results in 0.
-
Bring down: Bring down the next digit (5) from 25.
-
Divide: How many times does 2 go into 5? The answer is 2 with a remainder of 1. Write 2 above the 5.
-
Multiply: Multiply the quotient (2) by the divisor (2). This gives 4. Write 4 below the 5.
-
Subtract: Subtract 4 from 5. This results in a remainder of 1.
Therefore, 25 divided by 2 is 12 with a remainder of 1.
Method 2: Fractions
Another way to interpret 25 divided by 2 is as a fraction: 25/2. This fraction represents 25 parts of a whole divided into 2 equal parts. To simplify, we can perform the division:
25/2 = 12 1/2
This demonstrates that 25 divided by 2 equals 12 and a half. This is equivalent to the result obtained through long division, where the remainder represents the fractional part.
Method 3: Decimals
Converting the fraction 25/2 to a decimal provides another representation of the answer. To do this, we perform the division as follows:
25 ÷ 2 = 12.5
This confirms that 25 divided by 2 equals 12.5. This decimal representation is directly equivalent to the mixed number 12 1/2.
Understanding Remainders and Fractions
The remainder in long division (1 in this case) signifies the portion of 25 that is left over after dividing it into groups of 2. This remainder can be expressed as a fraction (1/2) or a decimal (0.5). The choice of representation—fraction, decimal, or mixed number—depends on the context of the problem and the desired level of precision.
Real-World Applications of Division and Remainders
The concept of division, particularly with remainders, permeates various aspects of daily life and specialized fields. Here are some examples:
-
Sharing: If you have 25 candies to share equally among 2 friends, each friend gets 12 candies, and you have 1 candy left over.
-
Measurement: Imagine cutting a 25-meter rope into 2-meter pieces. You'll get 12 pieces, with 1 meter remaining.
-
Programming: In computer programming, the remainder operator (%) (also called the modulo operator) is frequently used to determine if a number is even or odd, to control loops, and perform other computational tasks. For example,
25 % 2would return 1, indicating that 25 is odd. -
Engineering: Remainders play a crucial role in engineering design and manufacturing, ensuring efficient material utilization and precise measurements. Imagine fitting 25 square tiles onto a surface, where each tile is 2 units wide. This would involve careful consideration of spacing and any remaining space.
-
Finance: When dividing financial amounts, the remainder can represent cents or smaller currency units. For instance, splitting a $25 bill between two people results in $12.50 each.
Beyond the Basics: Extending the Concept
The seemingly simple calculation of 25 divided by 2 opens the door to more advanced mathematical concepts:
-
Modular Arithmetic: The remainder after division is central to modular arithmetic, a system where numbers "wrap around" after reaching a certain value (the modulus). This is used in cryptography and other areas of computer science.
-
Number Theory: Division, remainders, and related concepts are foundational to number theory, a branch of mathematics focused on the properties of numbers. Prime numbers, divisibility rules, and other important concepts are closely related to the process of division.
-
Algebra: Division is a crucial operation in algebraic manipulations. Solving equations often involves dividing both sides by a constant to isolate the variable.
-
Calculus: Although less direct, the concept of division underlies fundamental calculus concepts such as limits and derivatives. These concepts involve analyzing the behavior of functions as values approach zero or infinity, frequently requiring division to evaluate the function's behavior.
Frequently Asked Questions (FAQ)
-
What if I divide 25 by a number other than 2? The process remains the same. Use long division, fractions, or decimals to find the quotient and any remainder.
-
Why is the remainder important? The remainder represents the leftover amount after equal distribution, providing essential information in various applications.
-
Can I always express a remainder as a decimal? Yes, the remainder can always be expressed as a decimal by dividing the remainder by the divisor.
-
What if I'm dealing with very large numbers? Calculators or computer software can efficiently handle large numbers and complex division problems. Understanding the underlying principles remains crucial, however.
-
How does this relate to fractions and percentages? Division is fundamental to working with fractions and percentages. A fraction represents division, and calculating a percentage often involves division.
Conclusion
The seemingly simple operation of dividing 25 by 2 unveils a wealth of mathematical concepts and practical applications. From long division to fractions and decimals, multiple approaches yield the same answer (12.5 or 12 1/2), highlighting the interconnectedness of mathematical ideas. Understanding division, including the interpretation of remainders, is a crucial skill with wide-ranging implications in various fields. This comprehensive exploration aims to foster not only a deeper understanding of this specific calculation but also a more profound appreciation for the power and versatility of mathematics in our world. By grasping the nuances of division and its related concepts, you equip yourself with invaluable tools for problem-solving and critical thinking.
Latest Posts
Latest Posts
-
The Red Room Hg Wells
Sep 08, 2025
-
The Three Bears Story Book
Sep 08, 2025
-
How Much Is 32 Oz
Sep 08, 2025
-
What Is French For Baby
Sep 08, 2025
-
Mountain Range In South America
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 2 5 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.