2 2/5 As A Decimal
marihuanalabs
Sep 16, 2025 · 5 min read
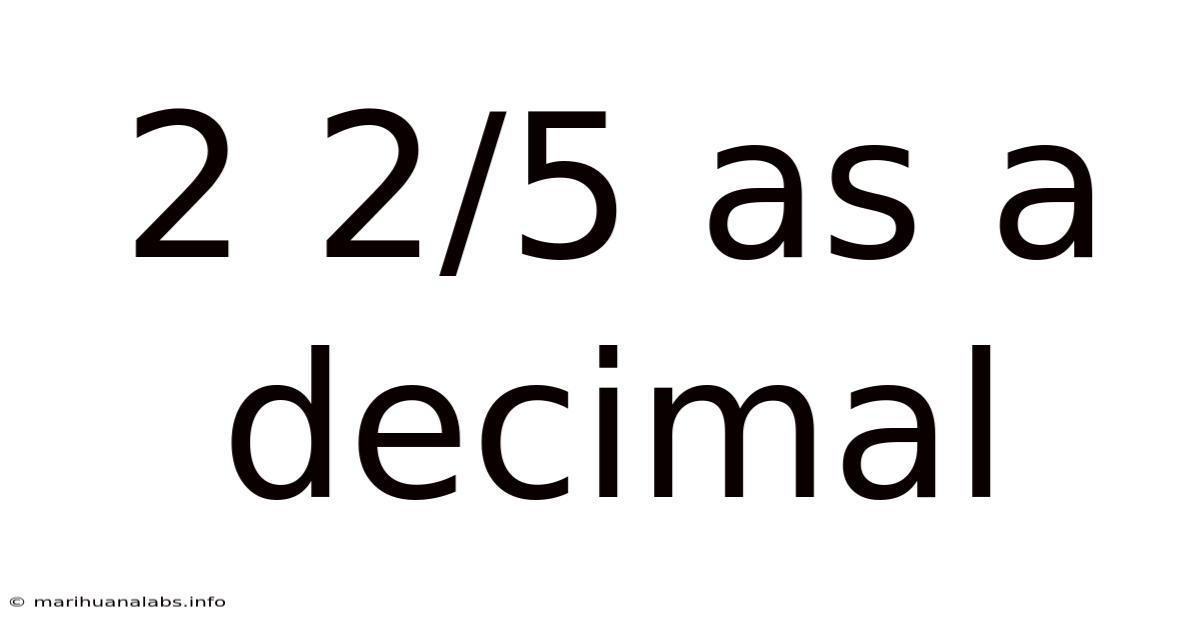
Table of Contents
Converting Fractions to Decimals: A Deep Dive into 2 2/5 as a Decimal
Converting fractions to decimals is a fundamental skill in mathematics, essential for various applications from everyday calculations to advanced scientific computations. This article will explore the process of converting the mixed number 2 2/5 into its decimal equivalent, providing a comprehensive understanding of the underlying principles and offering various methods to tackle similar conversions. We'll delve into the mechanics, explain the logic, and even touch upon the broader significance of this type of conversion in different mathematical contexts.
Understanding Fractions and Decimals
Before we dive into the conversion of 2 2/5, let's establish a clear understanding of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 2/5, 2 is the numerator and 5 is the denominator. This signifies two out of five equal parts.
A decimal is another way to represent a part of a whole, using the base-10 system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, 0.5 represents five-tenths (5/10), and 0.25 represents twenty-five hundredths (25/100).
Method 1: Converting the Mixed Number to an Improper Fraction
The mixed number 2 2/5 combines a whole number (2) with a fraction (2/5). To convert this to a decimal, we first need to transform it into an improper fraction. This involves converting the whole number into a fraction with the same denominator as the fractional part.
-
Convert the whole number to a fraction: The whole number 2 can be written as 2/1.
-
Find a common denominator: To add this to 2/5, we need a common denominator, which is 5. We multiply the numerator and denominator of 2/1 by 5: (2/1) * (5/5) = 10/5.
-
Add the fractions: Now, we add the two fractions: 10/5 + 2/5 = 12/5.
This gives us the improper fraction 12/5, representing the same value as the mixed number 2 2/5.
Method 2: Converting the Fraction to a Decimal by Division
The next step is converting the improper fraction 12/5 into a decimal. This is done by dividing the numerator (12) by the denominator (5).
-
Perform the division: 12 ÷ 5 = 2 with a remainder of 2.
-
Express the remainder as a decimal: The remainder 2 represents 2/5. To convert this to a decimal, we continue the division by adding a decimal point and a zero to the remainder: 20 ÷ 5 = 4.
-
Combine the whole number and decimal part: The whole number part of the division (2) is combined with the decimal part (0.4) to give the final answer: 2.4.
Therefore, 2 2/5 as a decimal is 2.4.
Method 3: Direct Conversion of the Fractional Part
This method focuses on converting the fractional part (2/5) to a decimal directly, and then adding the whole number. This often requires familiarity with common fraction-decimal equivalents.
Recognizing that 1/5 = 0.2, we can simply multiply this by 2 to get 2/5: 2 * 0.2 = 0.4. Adding the whole number 2, we again arrive at 2.4.
The Significance of Decimal Representation
The conversion of fractions to decimals is crucial for several reasons:
-
Comparability: Decimals allow for easier comparison of fractions. For instance, comparing 2 2/5 (2.4) to 2 1/2 (2.5) is simpler than comparing the fractions directly.
-
Calculations: Decimals are often more convenient for performing arithmetic operations like addition, subtraction, multiplication, and division, especially with the aid of calculators.
-
Real-world applications: Many real-world measurements and calculations utilize decimals, such as currency, weights, and measurements.
-
Data representation: Decimals are the preferred format for representing data in many fields, including science, engineering, and finance. Representing 2 2/5 as 2.4 makes it directly compatible with computer programs and databases designed for decimal input.
Illustrative Examples
Let's consider a few more examples to solidify the understanding:
-
Example 1: Converting 1 3/4 to a decimal:
- Convert to an improper fraction: (4/4) + (3/4) = 7/4
- Divide the numerator by the denominator: 7 ÷ 4 = 1.75 Therefore, 1 3/4 as a decimal is 1.75.
-
Example 2: Converting 3 1/8 to a decimal:
- Convert to an improper fraction: (24/8) + (1/8) = 25/8
- Divide the numerator by the denominator: 25 ÷ 8 = 3.125 Therefore, 3 1/8 as a decimal is 3.125.
Frequently Asked Questions (FAQ)
-
Q: What if the fraction doesn't divide evenly?
A: If the fraction doesn't divide evenly, you'll get a repeating or terminating decimal. For example, 1/3 equals 0.333... (a repeating decimal), while 1/4 equals 0.25 (a terminating decimal).
-
Q: Can I use a calculator to convert fractions to decimals?
A: Yes, most calculators have a fraction-to-decimal conversion function. Simply input the fraction and press the appropriate button.
-
Q: Why is converting fractions to decimals important?
A: It allows for easier comparison, simpler calculations, and compatibility with real-world applications and digital systems.
Conclusion
Converting fractions to decimals is a fundamental mathematical operation with widespread applications. We have explored several methods for converting 2 2/5 to its decimal equivalent (2.4), emphasizing the importance of understanding the underlying principles. By mastering this skill, you equip yourself with a valuable tool for various mathematical and real-world scenarios. Whether you utilize direct conversion methods or leverage the power of improper fractions and long division, the key is understanding the fundamental relationship between fractions and decimals. The ability to fluently convert between these representations is a crucial skill for anyone seeking to excel in mathematics and beyond. Remember to practice regularly to enhance your understanding and speed. Through consistent practice and a grasp of the underlying concepts, you'll confidently navigate the world of fractions and decimals.
Latest Posts
Latest Posts
-
Adjectives To Describe The City
Sep 16, 2025
-
What Does Mfc Stand For
Sep 16, 2025
-
Macbeth Sees Banquos Ghost Quote
Sep 16, 2025
-
Stave 2 Christmas Carol Summary
Sep 16, 2025
-
Determinants Of Supply In Economics
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 2 2/5 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.